2次関数のグラフ(放物線)がフリーハンドでうまく書けない・・・
放物線をキレイに見やすく書くのって難しいな〜
2次関数のグラフの簡単な書き方・裏ワザを教えてほしい!
こういった要望に応えます。
実は「2次関数のグラフ(放物線)をキレイに見やすく書くスキル」は、
2次関数の問題を解くうえで ものすごく重要 です。
数学において、図を「正確に」「見やすく」書ければ書けるほど問題が解きやすくなる、というのも事実です。
にも関わらず、「キレイで見やすい2次関数のグラフの簡単な書き方」を教えてくれる教師なんてあまりいませんよね?
そこで今回は、誰も教えてくれない「キレイで見やすい放物線の簡単な書き方」をレクチャーします!
まさに「裏ワザ」とも呼べる、この書き方を実際に私の生徒たちにも教えたところ、
2次関数のグラフを綺麗に見やすく、しかも素早く書くことができるようになりました。
その結果、2次関数の問題でしっかり点を取れる ようになりました。
ぜひあなたもこの方法をマスターしてみてください!
2次関数のグラフの簡単な書き方【放物線をキレイに見やすく書く裏ワザ】

それでは、2次関数のグラフを「簡単に」「素早く」「キレイに」書く裏ワザをお教えします。
- 平方完成する
- 頂点、軸、上or下に凸 を求める
- $y$切片を求める
- 放物線を書く ← Point!
- $y$軸を書く ← Point!
- $x$軸を書く ← Point!
前半(ステップ1〜3)は通常の書き方と同じですが、
後半(ステップ4〜6)が いつもと 逆 の流れですよね?
(ふつうは $x$軸 → $y$軸 → 放物線 の順番)
何てったって今回教えるのは「裏ワザ」ですから。ここが一番の肝となります。
この6ステップにしたがって、2次関数のグラフを一緒に書いてみましょう!
【ステップ1】平方完成する
まずは 平方完成 して「$y = a(x−p)^2 + q$」の形にします。
$ y = x^2 −4 x + 1 $
$ $ $ = (x −2)^2 −4 +1 $
$ $ $ = (x −2)^2 −3 $
「2次関数の平方完成のやり方」をおさらいしたい人はこちら。
二次関数の「平方完成」の計算に手間取ったり、しかもミスをよくしてしまう 平方完成を素早く、確実に、簡単に計算する方法を知りたい! そもそもなぜ平方完成するの? 平方完成はいつ使うの? 今回の記事では、こういった悩み・疑問[…]
【ステップ2】頂点、軸、上or下に凸 を求める
ステップ1で平方完成すると
「頂点」「軸」「上or下に凸」
が分かりますね。
2次関数 $ y = (x −2)^2 −3 $ のグラフは
$ \begin{cases}
頂点 \enspace (2, −3) \\
\\
軸:x = 2 \\
\\
下に凸 \\
\end{cases}$
の放物線。
【ステップ3】$y$切片を求める
$\color{red}{y}$切片 とは「$y$軸との交点の $y$座標」つまり「$x = 0$ となる $y$の値」です。
$y = x^2 −4 x + 1$ において
$x = 0$ のとき $y = 1$
よって、「$y$切片は $1$」と分かります。
つまり、点$(0, 1)$ を通るグラフということですね。
【ステップ4】放物線を書く
さて、ここからが いつもと逆のやり方 です。
書きたいグラフが「上に凸」か「下に凸」か を確認したら、
放物線を 一気に 書きます。
※ あまりゆっくり書いてしまうと、かえって線が歪みやすい

放物線をきれいに書くコツ・感覚 は人それぞれなので、
- 手を机から少し浮かせる
- 手首を固定する
- 肘を固定する
- 腕全体を使って書く
- 上半身をスライドしながら線をひく
- 腕の力をほどよく抜く
など、色々試してみてください。
【ステップ5】$y$軸を書く
「頂点」と「$\color{red}{y}$切片」の位置を考えながら、
「$y$軸」を書きます。
2次関数 $ y = (x −2)^2 −3 $ の場合、
- 頂点 $(2, −3)$
- $y$切片:$1$ → 点$(0, 1)$ を通る
ということを考慮すると
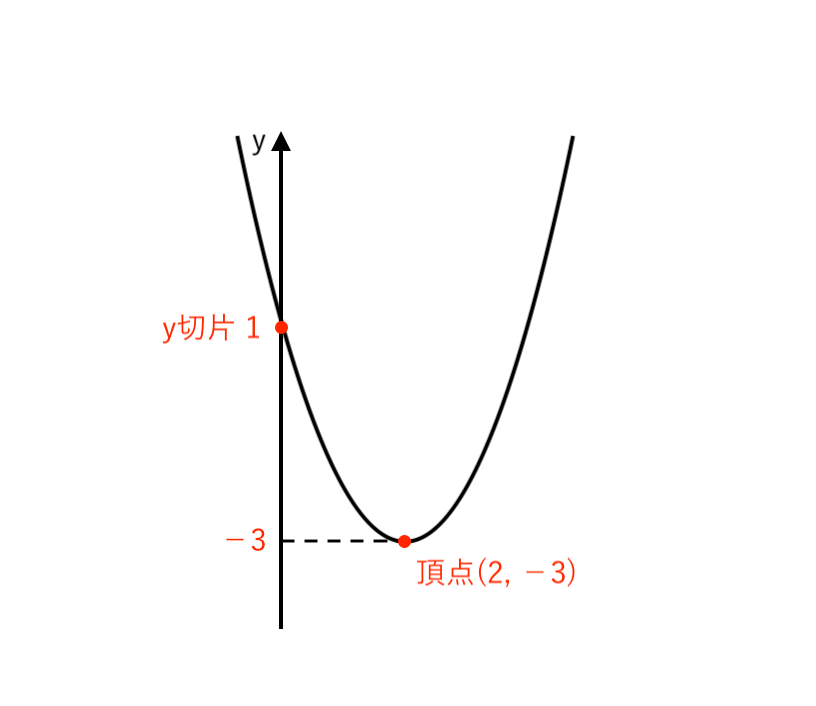
$y$軸は、だいたいこの辺りになりますね。
もうちょっと細かく説明すると
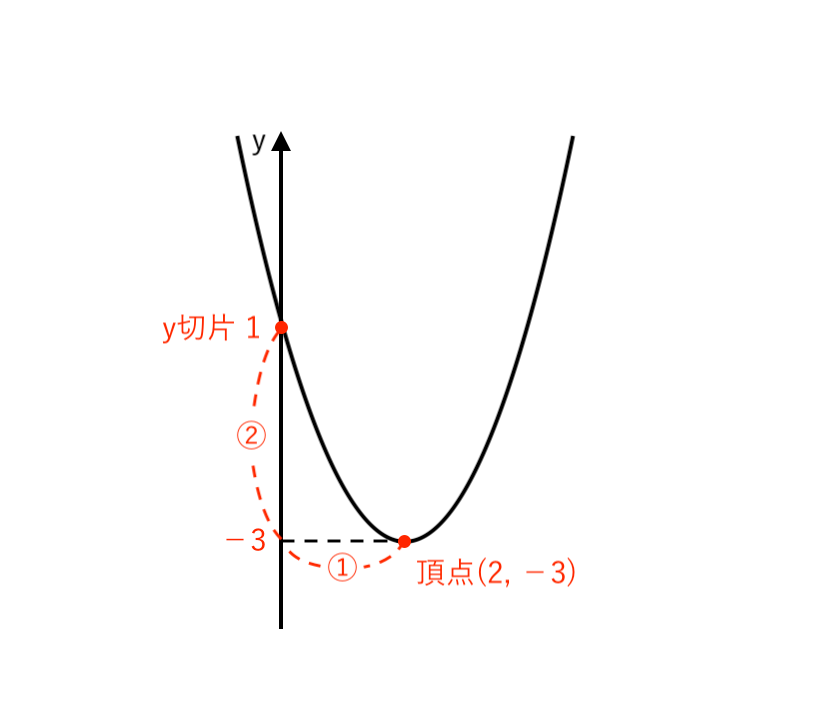
たて:よこ = 4:2 = ②:① くらいの比率になっていればPerfect!(あまりこだわらなくてもOK)
【ステップ6】$x$軸を書く
最後に「$x$軸」を書きます。
ポイントとしては、
$ $ 「$\color{red}{y}$切片」と「頂点の $\color{red}{y}$座標」
のバランスを考えて $x$軸 の位置を決定するとGood!
今回の場合、
- $y$切片:$1$
- 頂点の $y$座標:$−3$
この2点間の距離が
$ $ $1 − ( −3 ) = \color{red}{4} $
なので、$y = −3$ 〜 $1$ の間を 4等分 してから
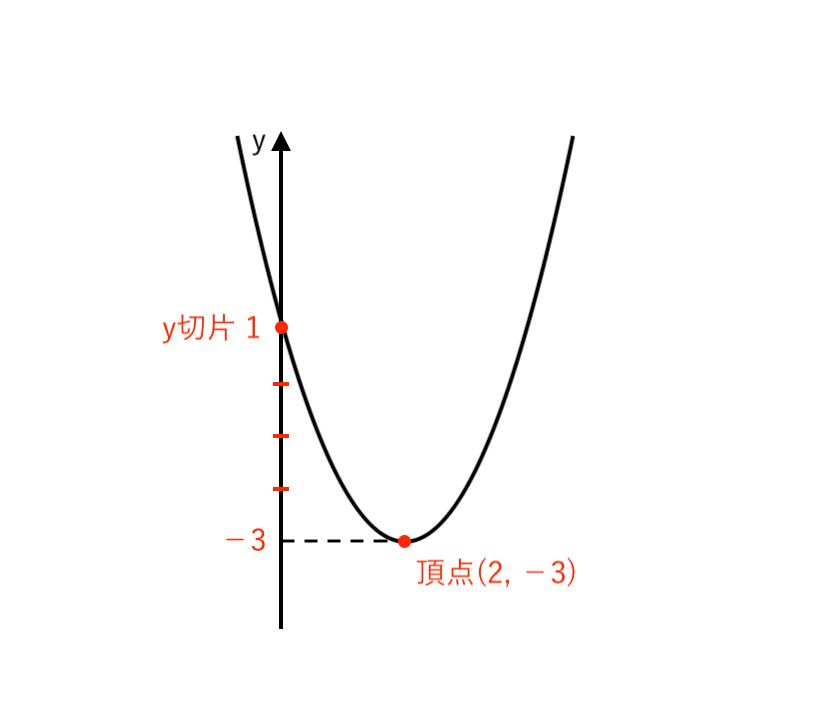
$y = 0$ のところに $x$軸 をひきます。
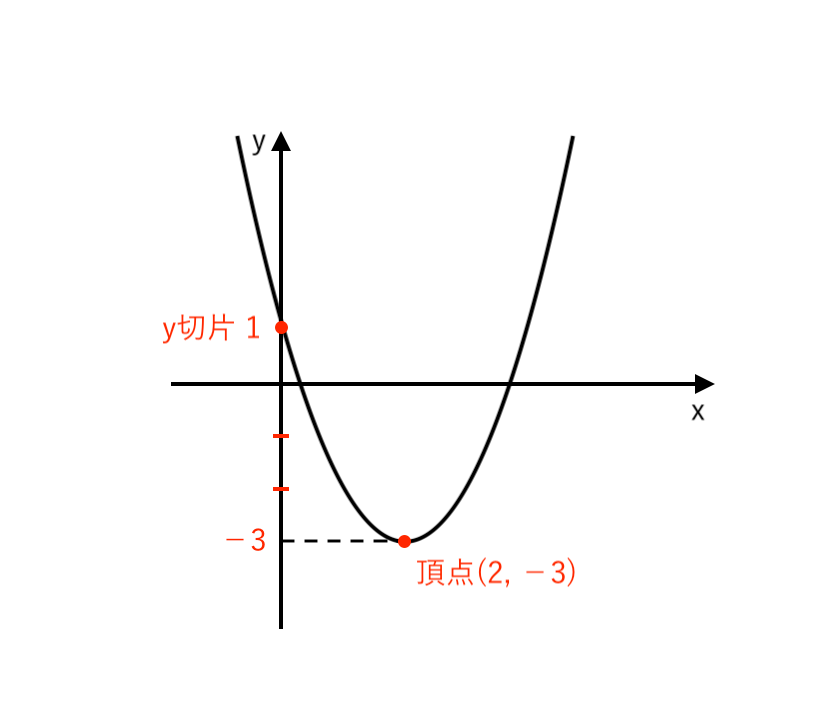
仕上げに「原点$O$」や「頂点の座標」などを書き込んだら、グラフの完成です!
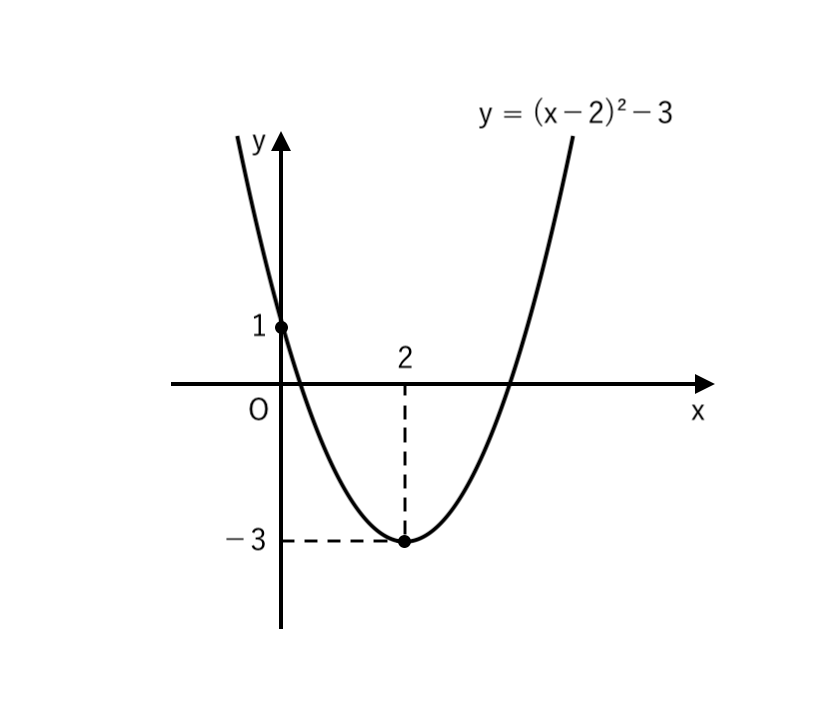
いかがでしたか? いつもよりキレイで見やすいグラフ が書けたと思いませんか?
なお、「たて:よこ」の比率は問題を解く上ではさほど重要ではないので、あまり気にしなくても大丈夫です。
他のパターンの放物線もやってみて、書き方に慣れていきましょう。
【練習問題】2次関数のグラフを見やすく書こう!
先ほどのグラフの書き方を真似して、見やすいグラフを書く練習をしてみましょう!
【問題】次の2次関数のグラフをかけ。
(1) $ y = x^2 −2x −1 $
(2) $ y = −x^2 + 2x + 2 $
(3) $ y = −x^2 −4x −5 $
(4) $ y = 2x^2 + 2x $
- 【解答】を見る
- 【解答】
(1)
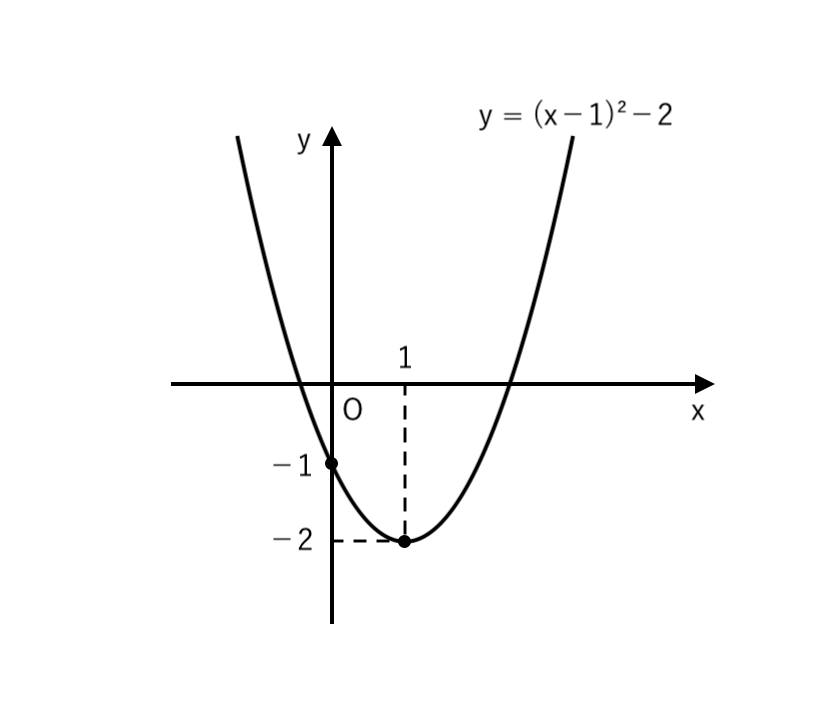
(2)
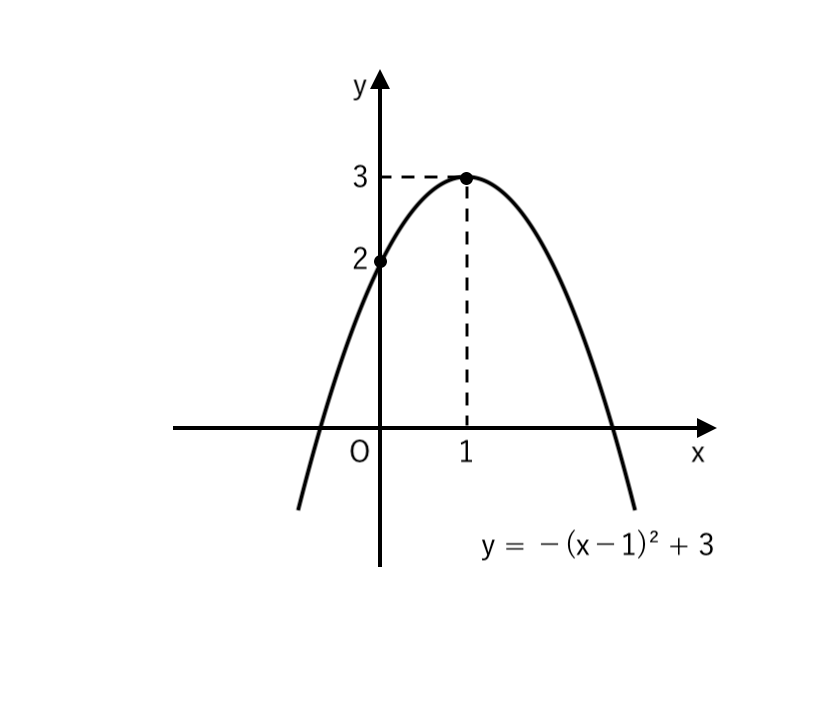
(3)
(4)
グラフを書くまでの過程(解説)はこちら。
- 【解説】を見る
- 【解説】
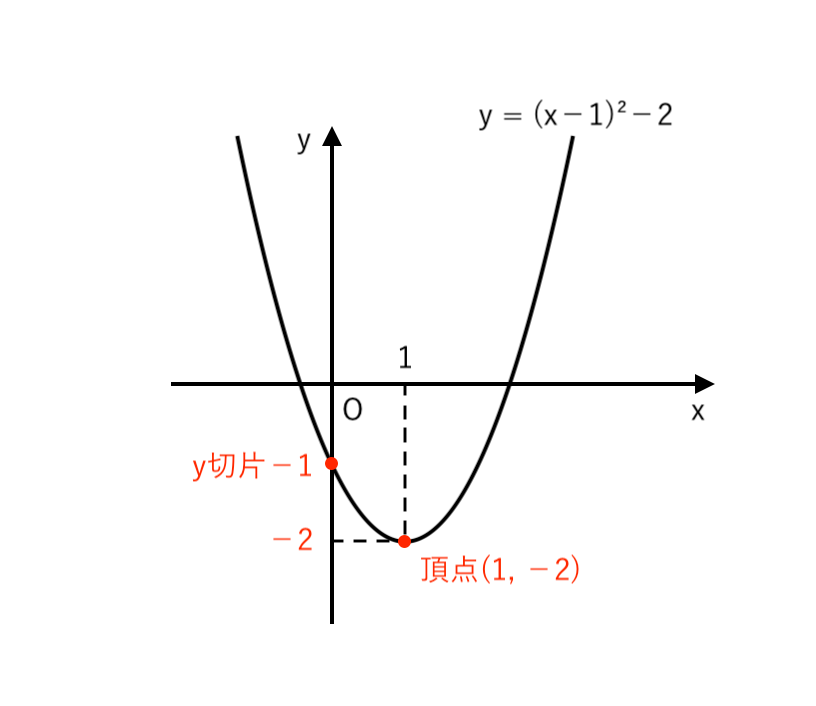
(1) $ y = x^2 −2x −1 $
$ $ $ = ( x −1 )^2 −2 $
∴ $ \begin{cases}
頂点 \enspace (1, −2) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線また、$x = 0$ のとき $y = −1 $
∴ $y$切片:$−1$
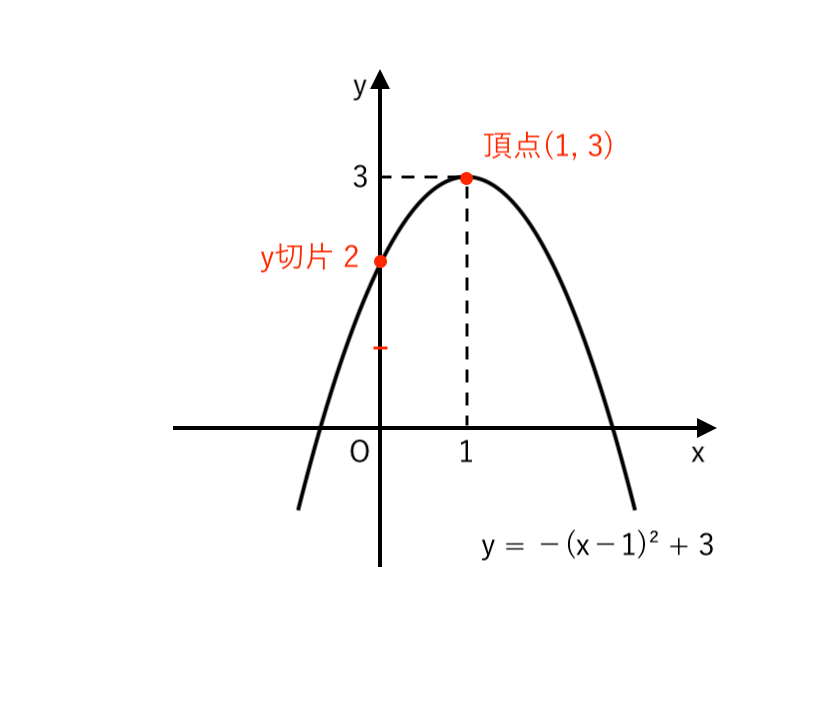
(2) $ y = −x^2 + 2x + 2 $
$ $ $ = −( x −1 )^2 + 3 $
∴ $ \begin{cases}
頂点 \enspace (1, 3) \\
\\
軸:x = 1 \\
\\
上に凸 \\
\end{cases}$ の放物線また、$x = 0$ のとき $y = 2 $
∴ $y$切片:$2$
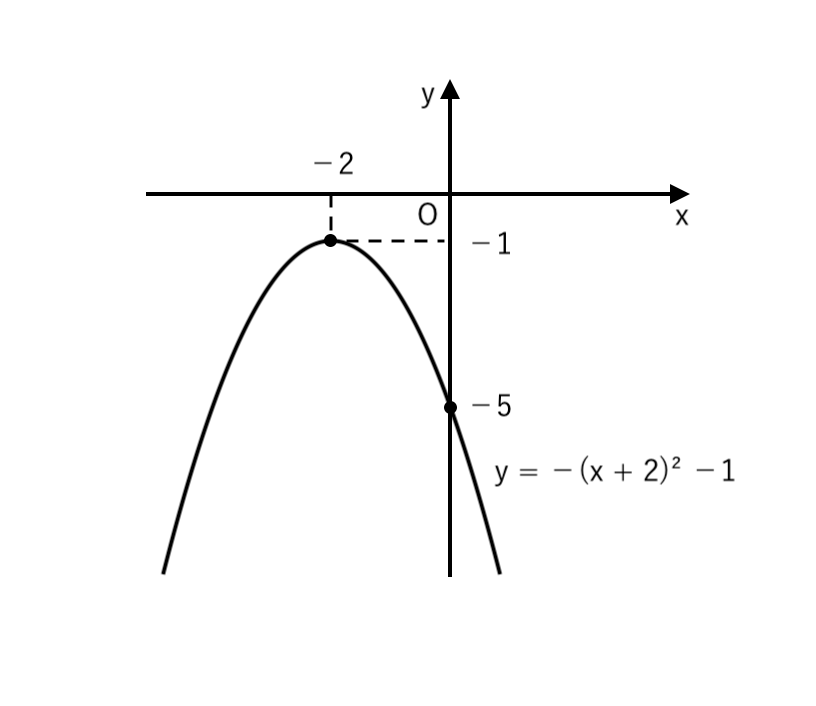
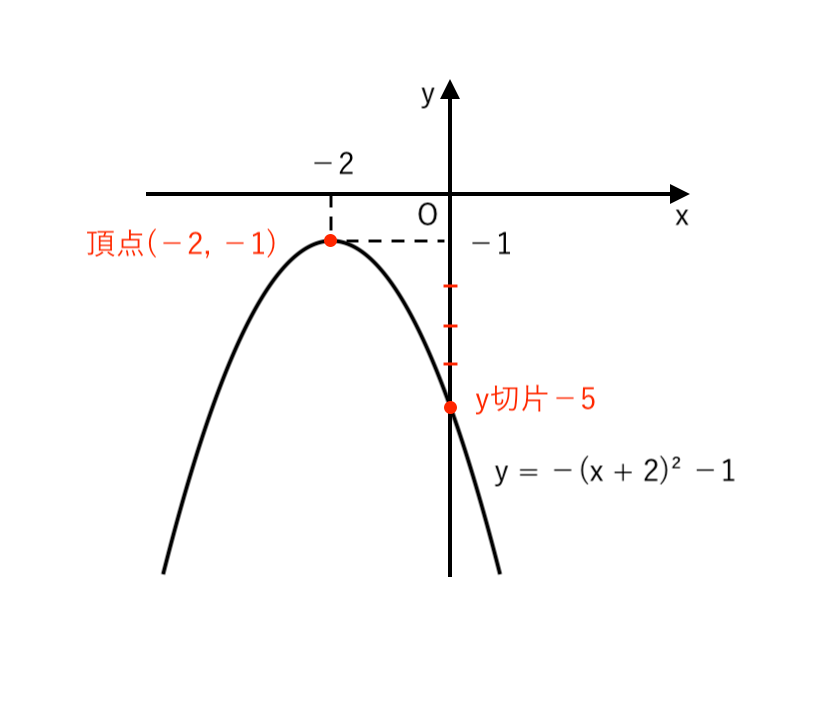
(3) $ y = −x^2 −4x −5 $
$ $ $ = −( x + 2 )^2 −1 $
∴ $ \begin{cases}
頂点 \enspace (−2, −1) \\
\\
軸:x = −2 \\
\\
上に凸 \\
\end{cases}$ の放物線また、$x = 0$ のとき $y = −5 $
∴ $y$切片:$−5$
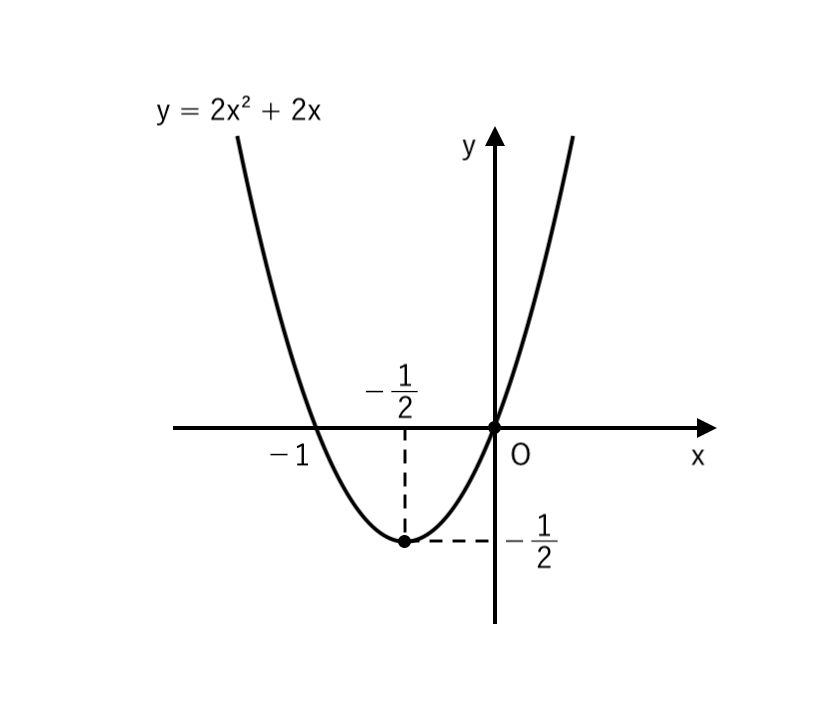
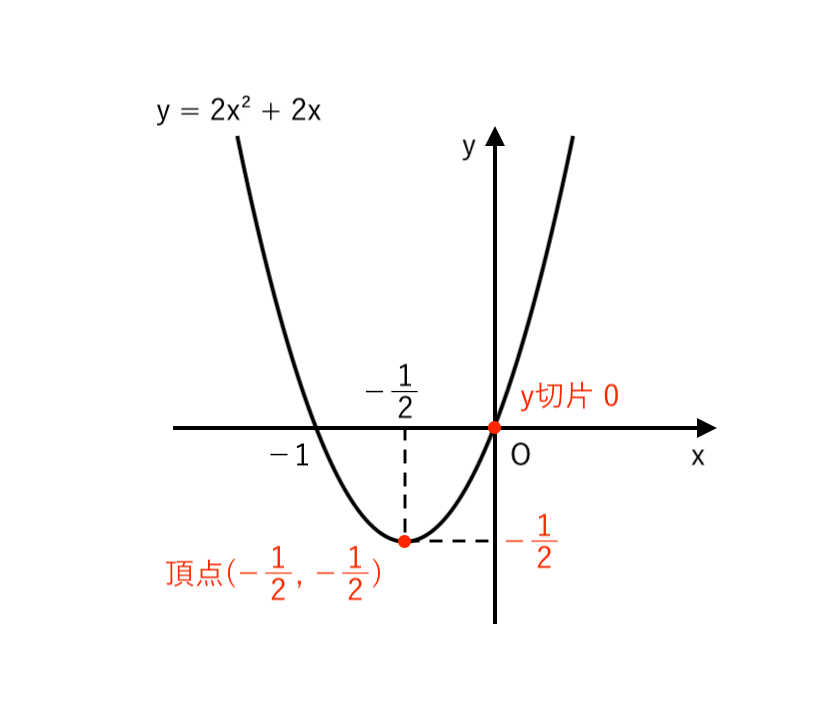
(4) $ y = 2x^2 + 2x $
$ $ $ \displaystyle { = 2 \left( x + {1 \over 2} \right)^2 −{1 \over 2} } $
∴ $ \begin{cases}
\displaystyle { 頂点 \enspace \left(−{1 \over 2} , −{1 \over 2} \right) } \\
\\
\displaystyle { 軸:x = −{1 \over 2} } \\
\\
下に凸 \\
\end{cases}$ の放物線また、$x = 0$ のとき $y = 0 $
∴ $y$切片:$0$ → 原点$O$ を通る
【まとめ】2次関数のグラフの簡単な書き方(裏ワザ)
今回は、2次関数のグラフを「簡単に」「素早く」「キレイに」書く裏ワザを紹介しました。
- 平方完成する
- 頂点、軸、上or下に凸 を求める
- $y$切片を求める
- 放物線を書く
- $y$軸を書く
- $x$軸を書く
ぜひ2次関数の問題を解くときに大いに役立ててください!
質問・要望があれば気軽にコメントください👍
【2次関数】頂点の座標が分数のグラフの書き方
2次関数で「頂点の座標が分数になる」とき、例えば
$ $ $ \displaystyle { y = \left( x + {5 \over 2} \right)^2 − {13 \over 4} } $
のようなグラフの書き方についてはこちら。
2次関数の頂点の座標が分数のとき、グラフはどうやって書けばいいの? 放物線の頂点が整数の場合、例えば3だったら素直に右に3マス進めばいいけど、分数の場合はどうなるの? こういった疑問に答えます。 2次関数で[…]
マイナスでくくる平方完成のやり方
$\displaystyle { y = \color{red}{−2}x^2 + 2x + 1}$ のように「$x^2$の係数が マイナス」のときの 平方完成 についてはこちら。
マイナスでくくるタイプの平方完成がうまくできない・・・ x²の係数がマイナス(負の値)のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 &nbs[…]
分数でくくる平方完成のやり方
$\displaystyle { y = \color{red}{2 \over 3}x^2 + 6x + 1}$ のように「$x^2$の係数が 分数」のときの 平方完成 についてはこちら。
分数でくくるタイプの平方完成がうまくできない・・・ x²の係数が分数のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 この記[…]
文字(定数)でくくる平方完成のやり方
$\displaystyle { y = \color{red}{a}x^2 + 2ax + 1}$ のように「$x^2$の係数が 文字」のときの 平方完成 についてはこちら。
aとかの文字(定数)でくくるタイプの平方完成がうまくできない・・・ x²の係数が文字(定数)のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 &[…]
質問・要望があれば気軽にコメントください👍