√(ルート)を含む数の「整数部分をa、小数部分をbとするとき〜」の問題の解き方をわかりやすく教えてほしい!
そもそも√の数の整数部分、小数部分ってのがイマイチ分からない・・・
どうやって考えたら解けるようになるの?
こういった疑問・要望にこたえます。
このページを読めば、
のようなパターンの問題を迷うことなくスラスラ解けるようになります。
√の数の整数部分・小数部分とは?

まずは、√(ルート)の数の整数部分・小数部分 のおさらいです。
【例題1-1】$ \sqrt{7}$ の整数部分、小数部分を求めよ。
もし $ \sqrt{7} = \color{red}{2}.\color{blue}{645 ⋯ } $ という近似値を覚えていれば、
・整数部分は $ \color{red}{2}$
・小数部分は $ \sqrt{7} − \color{red}{2}$
($ = \color{red}{2}.\color{blue}{645 ⋯ } − \color{red}{2} = 0. \color{blue}{645 ⋯ } $)
であっさり終わりです。
ですが、例えば $ \sqrt{19} $ とかになると、ほとんどの人は覚えてないですよね?
なので、次のやり方をマスターしておきましょう。
まず「$ \sqrt{7}$」を2乗した形「$7$」で考えます。
$○^2<7<□^2$ となるような数ではさむと
$○<\sqrt{7}<□$ と分かりますね。
【解答】
$4<7<9$ より
$ \sqrt{4}<\sqrt{7}<\sqrt{9} $
∴ $ 2<\sqrt{7}<3 $
$ \sqrt{7}$ が $2$ と $3$ の間にあることが分かりました。
これを 数直線で表す と
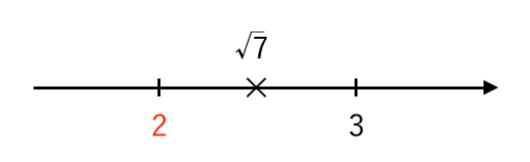
こんな感じなので、
$ $ $ \sqrt{7} = \color{red}{2} . \color{blue}{⋯} $
というところまでは言えますね。
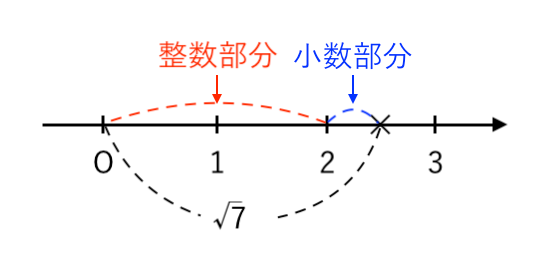
整数部分は、$\sqrt{7} $ を超えない最大の整数の「$\color{red}{2}$」です。
小数部分は、$\sqrt{7} $ から 整数部分の $\color{red}{2}$ を引いたものなので「$ \color{blue}{\sqrt{7} − 2} $」です。
よって、$ \sqrt{7} $ の
・整数部分は $\color{red}{2}$
・小数部分は $ \color{blue}{\sqrt{7} − 2} $
小数部分の求め方は、以下のように覚えておきましょう。
【例題1-2】$ \sqrt{10}$ の整数部分、小数部分を求めよ。
さっきと同じように考えてみます。
【解答】
$9<10<16$ より
$ \sqrt{9}<\sqrt{10}<\sqrt{16} $
∴ $ 3<\sqrt{10}<4 $
数直線で表すと
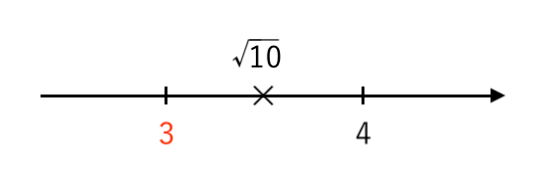
よって、$\sqrt{10}$ の
・整数部分は $\color{red}{3}$
・小数部分は $\sqrt{10}−3 $
ここまで理解できたら次に進みましょう。
a√b の整数部分・小数部分の求め方
次は、a√b の整数部分・小数部分 の求め方です。
【例題2-1】$ 2 \sqrt{5}$ の整数部分、小数部分を求めよ。
これは要注意! まずはよくあるダメな例から。
×【NG例】
$4<5<9$ より
$ \sqrt{4}<\sqrt{5}<\sqrt{9} $
∴ $ 2<\sqrt{5}<3 $
辺々に $2$ をかけて
∴ $ 4<2 \sqrt{5}<6 $
数直線で表すと
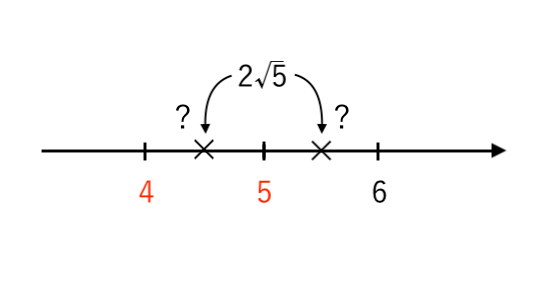
整数部分は・・・?
「あれ?整数部分って $4$ と $5$ のどっちだ?」となってしまい、上手くいきません。
というわけで、正しいやり方はこちら。
◎【解答】
$ 2 \sqrt{5} = \sqrt{20} $
$16<20<25$より
$ $ $ \sqrt{16}<\sqrt{20}<\sqrt{25} $
$ $ ∴ $ 4<\sqrt{20}<5 $
$ $ ∴ $ 4<2 \sqrt{5}<5 $
数直線で表すと
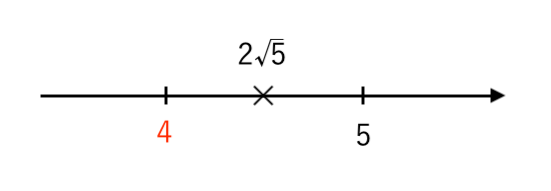
よって
・整数部分は $\color{red}{4}$
・小数部分は $ 2 \sqrt{5}−4 $
となり、正しく求められました。
a√b の整数部分・小数部分 の求め方をまとめると
−√a の整数部分・小数部分の求め方
次は、−√a の整数部分・小数部分 の求め方です。
【例題3-1】$ 5−\sqrt{6}$ の整数部分、小数部分を求めよ。
まずは「$ \sqrt{6} $ がどんな値か?」から考えます。
【解答】
$4<6<9$ より
$ $ $ \sqrt{4}<\sqrt{6}<\sqrt{9} $
$ $ ∴ $ 2<\sqrt{6}<3 $
辺々に $−1$ をかけて
$ $ $ −2>− \sqrt{6}>−3 $ ・・・(注)
$ $ ∴ $ −3<− \sqrt{6}<−2 $
辺々に $5$ を足して
$ $ $ 2<5 − \sqrt{6}<3 $
数直線で表すと
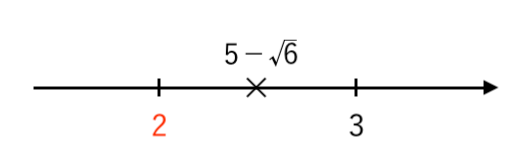
よって
・整数部分は $\color{red}{2}$
・小数部分は $ \left( 5 − \sqrt{6} \right)−2 = 3 − \sqrt{6} $
(注)不等式にマイナスの数をかけると、不等号の向きが逆になる
−√a の整数部分・小数部分 の求め方をまとめると
√を含む分数の整数部分・小数部分の求め方
次は、√(ルート)を含む分数の 整数部分・小数部分 を求めてみましょう。
【例題4-1】$ \displaystyle{ 5 + \sqrt{7} \over 2 } $ の整数部分、小数部分を求めよ。
分数が入っていて一見難しそうですが、やはり「$ \sqrt{7} $ がどんな値か?」からスタートしましょう。
【解答】
$4<7<9$ より
$ \sqrt{4}<\sqrt{7}<\sqrt{9} $
∴ $ 2<\sqrt{7}<3 $
ここから、少しづつ $ \displaystyle{ 5 + \sqrt{7} \over 2 } $ の形に近づけていきます。
辺々に $5$ を足して
$ $ $ 7<5 + \sqrt{7}<8 $
辺々を $2$ で割って
$ $ $ \displaystyle{ { 7 \over 2 } <{ 5 + \sqrt{7} \over 2 }< { 8 \over 2 } } $
$ $ ∴ $ \displaystyle{ 3 { 1 \over 2 } <{ 5 + \sqrt{7} \over 2 }< 4 } $ ・・・(注)
数直線で表すと
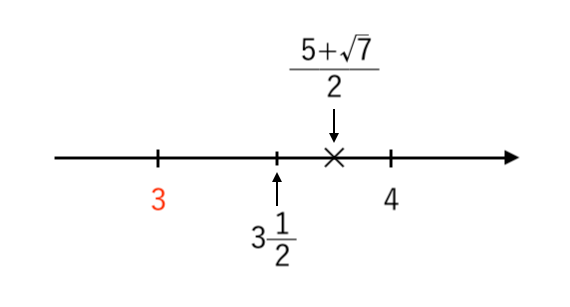
よって
・整数部分は $\color{red}{3}$
・小数部分は $ \displaystyle{ { 5 + \sqrt{7} \over 2 } −3 = { \sqrt{7} − 1 \over 2 } } $
(注)$ \displaystyle{ 7 \over 2 }$ のような分数は「帯分数に直す」のがオススメです。
わざわざ割り算をして「小数に直す」よりもラクに処理できます。
【例題4-2】$ \displaystyle{ 2 \over 3 − \sqrt{5} } $ の整数部分、小数部分を求めよ。
このままの形だと考えにくいので、分母の有理化 をします。
【解答】
$ \displaystyle{ 2 \over 3 − \sqrt{5} } $
$ = \displaystyle{ { 2 \over 3 − \sqrt{5} } × { 3 + \sqrt{5} \over 3 + \sqrt{5} } } $
$ = \displaystyle{ { 2 \left( 3 + \sqrt{5} \right) \over 9 − 5 } } $
$ = \displaystyle{ { 3 + \sqrt{5} \over 2 } } $
さっきと同じように「$ \sqrt{5} $ がどんな値か?」を考えます。
$4<5<9$ より
$ \sqrt{4}<\sqrt{5}<\sqrt{9} $
∴ $ 2<\sqrt{5}<3 $
ここから $ \displaystyle{ 3 + \sqrt{5} \over 2 } $ の形に持っていきます。
辺々に $3$ を足して
$ $ $ 5<3 + \sqrt{5}<6 $
辺々を $2$ で割って
$ $ $\displaystyle{ {5 \over 2}< { 3 + \sqrt{5} \over 2 } <{6 \over 2} }$
$ $ ∴ $\displaystyle{ 2 {1 \over 2}<{ 3 + \sqrt{5} \over 2 } <3 }$
数直線で表すと
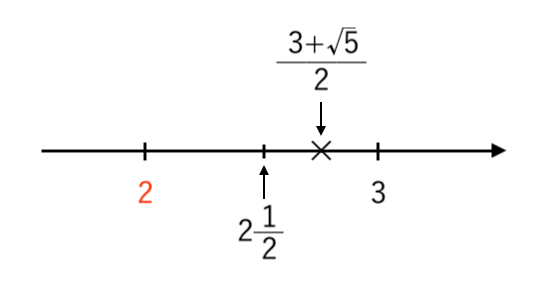
よって
・整数部分は $\color{red}{2}$
・小数部分は $\displaystyle{ { 3 + \sqrt{5} \over 2 } − 2 = { \sqrt{5} −1 \over 2 } }$
ここで、√(ルート)を含む分数について整数部分・小数部分 を求める手順をまとめておきます。
- 分母の有理化
- $n≦$(①の数)<$n+1$ を満たす整数 $n$ を見つける
- 整数部分は「$n$」
小数部分は「(①の数)$−n$」
この手順がイメージできるようになったら次に進みましょう!
√を含む分数の「整数部分をa、小数部分をbとするとき〜」応用問題 Lv.1
さて、いよいよ本題です。
√(ルート)を含む分数の「整数部分をa、小数部分をbとするとき〜」の 応用問題 Lv.1 です。
【問題1】$ \displaystyle{ 1 \over 2 − \sqrt{3} } $ の整数部分をa、小数部分をbとするとき、次の値を求めよ。
(1) $a, b$
ここまでの内容がちゃんと理解できているか?のチェックも兼ねて、
「整数部分a、小数部分bを求める」ところまで自力でやってみましょう!
- 【解答】を見る
-
【解答】
$ \displaystyle{ 1 \over 2 − \sqrt{3} } $
$ = \displaystyle{ { 1 \over 2 − \sqrt{3} } × { 2 + \sqrt{3} \over 2 + \sqrt{3} } } $
$ = \displaystyle{ 2 + \sqrt{3} } $
また、$1<3<4$ より
$ $ $ \sqrt{1}<\sqrt{3}<\sqrt{4} $
$ $ ∴ $ 1<\sqrt{3}<2 $
辺々に $2$ を足して
$ $ $ 3<2 + \sqrt{3}<4 $
数直線で表すと
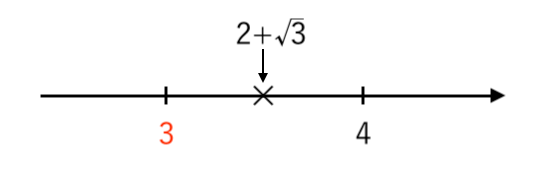
よって
・整数部分 $a = \color{red}{3} $
・小数部分 $b = \left( 2 + \sqrt{3} \right)− 3 = \sqrt{3} − 1 $
(2) $a^2+2ab+3b^2$
(1) で求めた $a,b$ の値をそのまま代入すればOKです。
実際に手を動かして解いてみましょう。
- 【解答】を見る
-
【解答】
$a^2+2ab+3b^2$
$ = 3^2+2 \cdot 3 \cdot \left( \sqrt{3} − 1 \right) + 3 \left( \sqrt{3} − 1 \right)^2$
$ = 9 + 6 \sqrt{3} − 6 + 3 \left( 4 −2 \sqrt{3} \right) $
$ = 9 + 6 \sqrt{3} − 6 + 12 −6 \sqrt{3} $
$ = 15 $
(3) $ \displaystyle{ { 1 \over a−b−1 } − { 1 \over a+b+1 } } $
これも $a,b$ の値を代入してみましょう。
- 【解答】を見る
-
【解答】
$\displaystyle{ { 1 \over a−b−1 } − { 1 \over a+b+1 } } $
$= \displaystyle{ { 1 \over 3−\left( \sqrt{3} − 1 \right)−1 } − { 1 \over 3+\left( \sqrt{3} − 1 \right)+1 } } $
$= \displaystyle{ { 1 \over 3− \sqrt{3} } − { 1 \over 3 + \sqrt{3} } } $
$= \displaystyle{ { \require{cancel} \bcancel{3} + \sqrt{3} \over 6 } − { \bcancel{3}− \sqrt{3} \over 6 } } $
$= \displaystyle{ { 2 \sqrt{3} \over 6 } } $
$= \displaystyle{ { \sqrt{3} \over 3 } } $
ここまで自力で解けるようになっていれば、学校の中間・期末テストならまず安心です。
自信を持ってくださいね!
√を含む分数の「整数部分をa、小数部分をbとするとき〜」応用問題 Lv.2
入試問題にチャレンジしたい!という人は、こちらもぜひやってみてください。
√(ルート)を含む分数の「整数部分をa、小数部分をbとするとき〜」の 応用問題 Lv.2 です。 [17 名城大・改]
【問題2】$\displaystyle{ \sqrt{2} \over \sqrt{2}−1 }$ の整数部分をa、小数部分をbとするとき
(1) $a, b$ の値を求めよ。
まずは 分母の有理化 をして、整数部分と小数部分を求めましょう。
- 【解答】を見る
-
【解答】
$\displaystyle{ \sqrt{2} \over \sqrt{2}−1 }$
$ = \displaystyle{ { \sqrt{2} \over \sqrt{2}−1 }×{ \sqrt{2} + 1 \over \sqrt{2} + 1 } }$
$ = \displaystyle{ { \sqrt{2} ( \sqrt{2} + 1 ) \over 2 − 1 } }$
$ = \displaystyle{ 2 + \sqrt{2} }$
また、$1<2<4$ より
$ $ $ \sqrt{1}<\sqrt{2}<\sqrt{4} $
$ $ ∴ $ 1<\sqrt{2}<2 $
辺々に $2$ を足して
$ $ $ 3<2 + \sqrt{2}<4 $
よって
・整数部分 $a = 3$
・小数部分 $b = \left( 2 + \sqrt{2} \right) − 3 = \sqrt{2} − 1 $
(2) $\displaystyle{ x = a − {1 \over b} } $ の値を求めよ。
(1) で求めた $a, b$ の値を代入します。
- 【解答】を見る
-
【解答】
$\displaystyle{ x = a − {1 \over b} } $
$ $ $\displaystyle{ = 3 − {1 \over \sqrt{2} − 1 } } $
$ $ $\displaystyle{ = 3 − {1 \over \sqrt{2} − 1 }×{ \sqrt{2} + 1 \over \sqrt{2} + 1 } } $
$ $ $\displaystyle{ = 3 − { \sqrt{2} + 1 \over 2 − 1 } } $
$ $ $\displaystyle{ = 3 − \left( \sqrt{2} + 1 \right) } $
$ $ $\displaystyle{ = 2 − \sqrt{2} } $
(3) $ x^4 −5x^3 + 4x^2 + 6x $ の値を求めよ。
(2) の結果を利用して「$x^2=$($x$ の1次式)」で表せたら、$x$ の 次数を下げる ことができます。
- 【解答】を見る
-
【解答】
(2) より
$ $ $\displaystyle{ x = 2 − \sqrt{2} } $
$ $ ∴ $\displaystyle{ x − 2 = − \sqrt{2} } $
両辺を $2$乗して
$ $ $\displaystyle{ ( x − 2 )^2 = \left(− \sqrt{2} \right)^2 } $
$ $ ∴ $\displaystyle{ x^2 −4x + 4 = 2 } $
$ $ ∴ $\displaystyle{ x^2 = 4x − 2 } $ ・・・①
よって
・$x^3 = x( \color{red}{x^2} )$
$ $ $= x( \color{red}{4x − 2} )$ (①を代入)
$ $ $ = 4 \color{red}{x^2} − 2x$
$ $ $ = 4( \color{red}{4x − 2} ) − 2x$ (①を代入)
$ $ $ = 14x − 8 $ ・・・②
・$x^4 = x( \color{blue}{x^3} )$ ・・・(注)
$ $ $ = x( \color{blue}{14x − 8} )$ (②を代入)
$ $ $ = 14 \color{red}{x^2} − 8x $
$ $ $ = 14 ( \color{red}{4x − 2} ) − 8x $ (①を代入)
$ $ $ = 48x − 28 $ ・・・③
①、②、③より
$ $ $ x^4 −5x^3 + 4x^2 + 6x $
$ $ $ = (48x − 28) −5(14x − 8) + 4(4x − 2) + 6x $
$ $ $ = (48x − 28) −5(14x − 8) + 4(4x − 2) + 6x $
$ $ $ = 4 $
(注)$x^4 = \left(x^2 \right)^2 = ( 4x − 2 )^2 = 16x^2 −16x + 4 = ⋯ $ と考えてもOK
別解として、数学Ⅱで学習する「整式の割り算」を利用するやり方もあります。
- 【別解】を見る
-
【別解】
$\displaystyle{ x^2 = 4x − 2 } $ より
$ $ $\displaystyle{ x^2 − 4x + 2 = 0 } $
$ x^4 −5x^3 + 4x^2 + 6x $ を $x^2 − 4x + 2 $ で割ると
$ x^4 −5x^3 + 4x^2 + 6x $
$ = \left( x^2 − 4x + 2 \right) \left( x^2 − x − 2 \right) + 4 $
$ = \require{cancel} \bcancel{ 0 \cdot \left( x^2 − x − 2 \right) } + 4 $ ($ x^2 − 4x + 2 = 0$ を代入)
$ = 4 $
以上、Lv.2 の応用問題でした。
√を含む分数の「整数部分をa、小数部分をbとするとき〜」応用問題 Lv.3
いよいよラスト。
√(ルート)を含む分数の「整数部分をa、小数部分をbとするとき〜」の 応用問題 Lv.3 に挑戦です。 [センター試験追試・改]
【問題3】$ \displaystyle{ x = { 1 + 2 \sqrt{5} \over 8 − 3 \sqrt{5} } } $ の整数部分をa、小数部分をbとするとき
(1) $a, b$ を求めよ。
まずは 分母の有理化 からスタートです。
- 【解答】を見る
-
【解答】
$ \displaystyle{ x = { 1 + 2 \sqrt{5} \over 8 − 3 \sqrt{5} } } $
$ $ $ \displaystyle{ = { 1 + 2 \sqrt{5} \over 8 − 3 \sqrt{5} } × { 8 + 3 \sqrt{5} \over 8 + 3 \sqrt{5} } } $
$ $ $ \displaystyle{ = { \left(1 + 2 \sqrt{5} \right) \left( 8 + 3 \sqrt{5} \right) \over 64 − 45 } } $
$ $ $ \displaystyle{ = { 38 + 19 \sqrt{5} \over 19 } } $
$ $ $ \displaystyle{ = 2 + \sqrt{5} } $
また、$4<5<9$ より
$ $ $ \sqrt{4}<\sqrt{5}<\sqrt{9} $
$ $ ∴ $ 2<\sqrt{5}<3 $
辺々に $2$ を足して
$ $ $ 4<2 + \sqrt{5}<5 $
よって
・整数部分 $a = 4$
・小数部分 $b = \left( 2 + \sqrt{5} \right) − 4 = \sqrt{5} − 2 $
(2) $x^2 + b^2 $ を求めよ。
$x$、$b$ の値を代入します。
- 【解答】を見る
-
【解答】
$x^2 + b^2 $
$= \left( 2 + \sqrt{5} \right)^2 + \left( \sqrt{5} − 2 \right)^2 $
$= 9 + \require{cancel} \bcancel{ 4 \sqrt{5} } + 9 − \bcancel{ 4 \sqrt{5} } $
$= 18 $
(3) $x^2 − b^2 $ を求めよ。
こちらも代入すればOK。
- 【解答】を見る
-
【解答】
$x^2 − b^2 $
$= (x + b) (x − b) $
$= (x + b) a $
$= \left\{ \left( \require{cancel} \bcancel{2} + \sqrt{5} \right) + \left( \sqrt{5} − \bcancel{2} \right) \right\} \cdot 4 $
$= 2 \sqrt{5} \cdot 4 $
$= 8 \sqrt{5} $
(4) 等式 $ \displaystyle{ \left( { x^2 + b^2 \over 2 } \right)^m + \left( { x^2 − b^2 \over 2 } \right)^n = 809 } $ を満たす自然数 $m, n$ の値を求めよ。
ひとまず (1)、(2) の結果を代入すると方向性が見えてきます。
- 【解答・解説】を見る
-
【解答】
$ \displaystyle{ \left( { x^2 + b^2 \over 2 } \right)^m + \left( { x^2 − b^2 \over 2 } \right)^n = 809 } $
に (1)、(2) の結果を代入して
$ $ $ \displaystyle{ \left( { 18 \over 2 } \right)^m + \left( { 8 \sqrt{5} \over 2 } \right)^n = 809 } $
$ $ ∴ $ \displaystyle{ 9^m + \left( 4 \sqrt{5} \right)^n = 809 } $ ・・・①
$ $ ∴ $ \displaystyle{ \left( 4 \sqrt{5} \right)^n = 809 − 9^m } $ ・・・②
②について、右辺が有理数より、左辺も有理数。 ・・・(注1)
よって、$n$ は偶数なので $n = 2k$($k$:自然数)とおける。 ・・・(注2)
これを①に代入して
$ $ $ \displaystyle{ 9^m + \left( 4 \sqrt{5} \right)^{2k} = 809 } $
$ $ ∴ $ \displaystyle{ 9^m + 80^k = 809 } $ ・・・③
$ $[1] $k=1$ のとき
$ $ ③より
$ $ $ \displaystyle{ 9^m + 80 = 809 } $
$ $ ∴ $ \displaystyle{ 9^m = 729 } $
$ $ ∴ $m = 3$(自然数より適する)
$ $ このとき、$n=2 \cdot 1 = 2$
$ $[2] $k≧2$ のとき
$ $ ③より
$ \displaystyle{ \color{red}{809} = 9^m + 80^k \color{red}{≧} 9^m + 80^2 = \color{red}{9^m + 6400} } $
$ $ ∴ $ \displaystyle{ 809 ≧ 9^m + 6400 } $
これを満たす自然数 $m$ は存在しない(不適)
$ $[1]、[2]より
$ $ $m = 3,$ $n=2$
(注1)左辺と右辺を比較するやり方は「背理法」のところでも出てきました。
関連記事今回の記事は、次のような疑問を持っている人のために書きました。 背理法の使い方・考え方がいまいち分からない 背理法をいつ、どんな問題で使えばいいの? そもそも背理法って何? 正直、意味不明だ・・・ 元の命題がそのまま証明しに[…]
(注2)偶数乗のときだけ「$\left( 4 \sqrt{5} \right)^n$」の√が外れます。
$ $ 例:$\left( 4 \sqrt{5} \right)^2 = 4^2 × \sqrt{5}^2 = 16 × 5$
以上です。お疲れ様でした!
最後に
√(ルート)を含む分数の「整数部分をa、小数部分をbとするとき〜」の問題は、学校のテスト や 大学入試 でもよく出ます。
a√b、−√a などのパターンにも対応できるようにしっかり練習しておきましょう!
質問・要望があれば気軽にコメントください👍

