sinとcosの変換公式がなかなか覚えられない!
いちいち単位円をかいて変換公式を導くのも面倒だ・・・
sinとcosの変換を一瞬で&簡単にできる便利な方法はないの?
こういった要望に応えます。
この記事を読めば、
- $\sin 130^\circ = \cos$
- $-\cos 20^\circ =$ $110^\circ$
- $\sin (\theta + 90^\circ) =$ $\theta$
- $-\cos (\theta − 270^\circ) =$ $\theta$
このような sin と cos の変換が ほんの2〜3秒でできる ようになります。
この「裏ワザ」を 知っているか知らないかで大きく差がつく ので、計算スピードを大幅に上げたい人は最後まで読むのをおすすめします。
sinとcosの変換公式は覚えにくい!
sinとcosの変換公式 は以下のようにたくさんあって、ハッキリ言って覚えにくいですよね。
✔︎ $\sin \theta$
$=\cos(90^\circ – \theta)$
$=-\cos(\theta + 90^\circ)$
$=\sin(180^\circ – \theta)$
$=-\sin(180^\circ + \theta)$
$=-\cos(270^\circ – \theta)$
$=\cos(\theta – 90^\circ)$
$=-\sin(- \theta)$
✔︎ $\cos \theta$
$=\sin(90^\circ – \theta)$
$=\sin(\theta + 90^\circ)$
$=-\cos(180^\circ – \theta)$
$=-\cos(180^\circ + \theta)$
$=-\sin(270^\circ – \theta)$
$=-\sin(\theta – 90^\circ)$
$=\cos(- \theta)$
「sinとcosの変換公式は単位円をかいて導けばいいんだよ」と言っている人もいますが、
テスト中にいちいち単位円で確認していては時間がもったいないです。
そこで、今回紹介する「裏ワザ」の登場です。
sinとcosの変換を一瞬で&簡単にやる「裏ワザ」
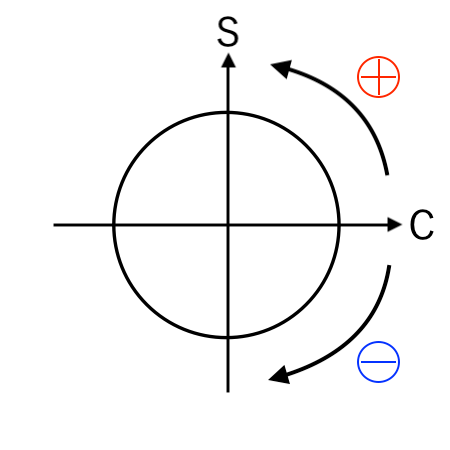
sinとcosの変換 を一瞬で簡単にやる「裏ワザ」を説明します。
上図の見方は、次の通り。
【軸】
- 横軸:C(cos)
- 縦軸:S(sin)
【角度の回転】
- 反時計回り(左回り) → プラス
- 時計回り(右回り) → マイナス
実際の使い方を見ていきましょう。
sin と cos の変換【90°回転】
例:sin から −cos に変換(+90°)
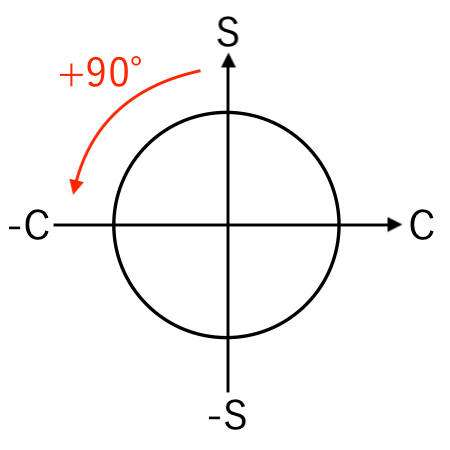
$\sin($ $\theta − 90^\circ$ $)$
$=$ $\theta$
$「 $$\theta − 90^\circ$$ 」$ を $「 $$\theta$$」$にしたい($−90^\circ$を消したい)とき、
すると、
−C(−cos)
に移るので
となります。
例:cos から sin に変換(+90°)
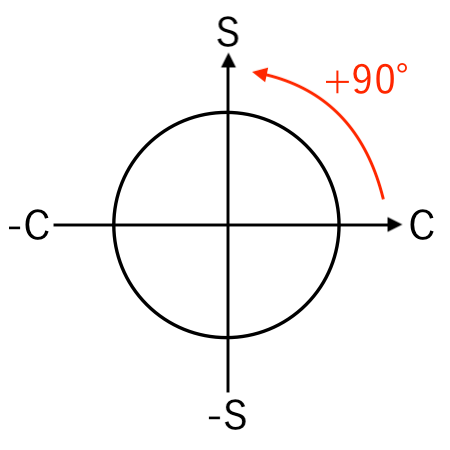
$\cos($ $\theta − 90^\circ$ $)$
$=$ $\theta$
$「 $$\theta − 90^\circ$$ 」$ を $「 $$\theta$$」$にしたい($−90^\circ$を消したい)とき、
すると、
S(sin)
に移るので
となります。
例:sin から cos に変換(−90°)
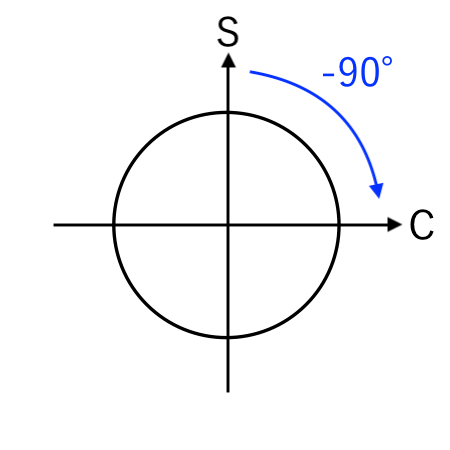
$\sin($ $\theta + 90^\circ$ $)$
$=$ $\theta$
$「 $$\theta + 90^\circ$$ 」$ を $「 $$\theta$$」$にしたい($+90^\circ$を消したい)とき、
すると、
C(cos)
に移るので
となります。
例:cos から −sin に変換(−90°)
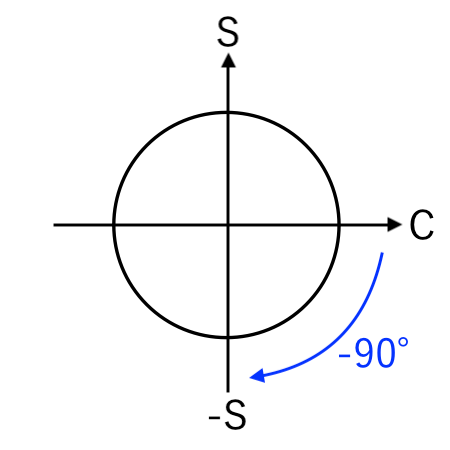
$\cos($ $\theta + 90^\circ$ $)$
$=$ $\theta$
$「 $$\theta + 90^\circ$$ 」$ を $「 $$\theta$$」$にしたい($+90^\circ$を消したい)とき、
すると、
−S(−sin)
に移るので
となります。
例:−sin から cos に変換(+90°)
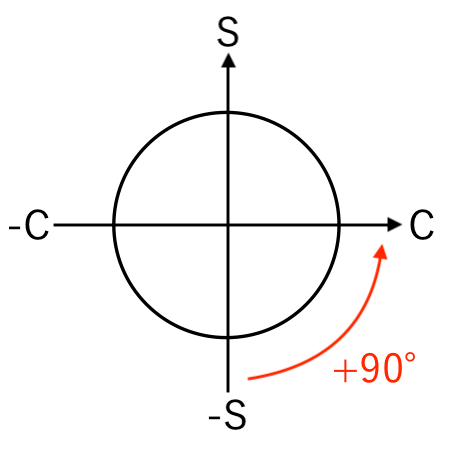
$-\sin($ $\theta − 90^\circ$ $)$
$=$ $\theta$
$「 $$\theta − 90^\circ$$ 」$ を $「 $$\theta$$」$にしたい($−90^\circ$を消したい)とき、
すると、
C(cos)
に移るので
となります。
「$-\sin$」の「$-$(マイナス)」も取れて一石二鳥ですね!
その他の例(90°回転)
以下の計算も同様です。自由自在に変換OK!
$-\sin($ $\theta + 90^\circ$$)$ $= -\cos\theta$
・・・「−S」から $-90^\circ$回転 →「−C」
$-\cos($ $\theta − 90^\circ$$)$ $= -\sin\theta$
・・・「−C」から $+90^\circ$回転 →「−S」
$-\cos($ $\theta + 90^\circ$$)$ $= \sin\theta$
・・・「−C」から $-90^\circ$回転 →「S」
$\sin$ $130^\circ$ $= \cos 40^\circ$
・・・「S」から $-90^\circ$回転 →「C」
$\cos$ $(-70^\circ)$ $= \sin 20^\circ$
・・・「C」から $+90^\circ$回転 →「S」
$\sin($ $\theta + 150^\circ$$)$ $= \cos(\theta + 60^\circ)$
・・・「S」から $-90^\circ$回転 →「C」
sin と cos の変換【180°回転】
例:cos から −cos に変換(+180°)
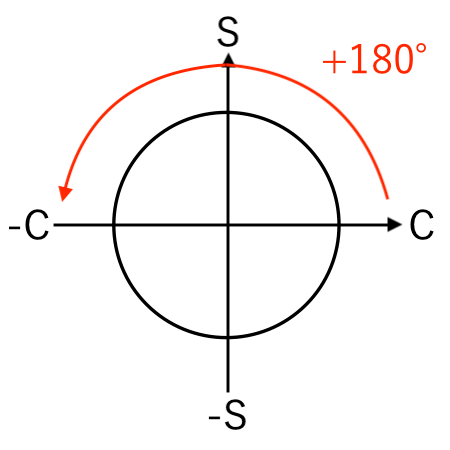
$\cos($ $\theta − 180^\circ$ $)$
$=$ $\theta$
$「 $$\theta − 180^\circ$$ 」$ を $「 $$\theta$$」$にしたい($−180^\circ$を消したい)とき、
すると、
−C(−cos)
に移るので
となります。
例:−sin から sin に変換(−180°)
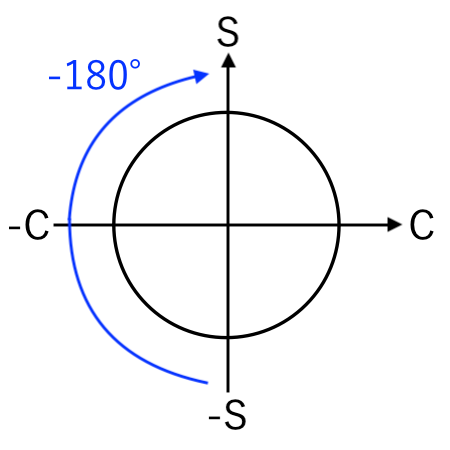
$-\sin($ $\theta + 180^\circ$ $)$
$=$ $\theta$
$「 $$\theta + 180^\circ$$ 」$ を $「 $$\theta$$」$にしたい($+180^\circ$を消したい)とき、
すると、
S(sin)
に移るので
となります。
その他の例(180°回転)
以下の計算も同様です。自由自在に変換OK!
$\sin($ $\theta + 180^\circ$$)$ $= -\sin\theta$
・・・「S」から $-180^\circ$回転 →「−S」
$-\cos($ $\theta – 180^\circ$$)$ $= \cos\theta$
・・・「−C」から $+180^\circ$回転 →「C」
$-\cos($ $\theta + 180^\circ$$)$ $= \cos\theta$
・・・「−C」から $-180^\circ$回転 →「C」
$\sin$ $220^\circ$ $= -\sin 40^\circ$
・・・「S」から $-180^\circ$回転 →「−S」
$\cos$ $(-110^\circ)$ $= -\cos 70^\circ$
・・・「C」から $+180^\circ$回転 →「−C」
$\sin($ $\theta + 225^\circ$$)$ $= -\sin(\theta + 45^\circ)$
・・・「S」から $-180^\circ$回転 →「−S」
sin と cos の変換【270°回転】
例:sin から cos に変換(+270°)
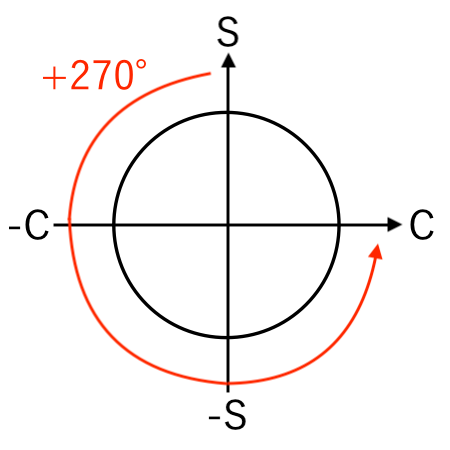
$\sin($ $\theta − 270^\circ$ $)$
$=$ $\theta$
$「 $$\theta − 270^\circ$$ 」$ を $「 $$\theta$$」$にしたい($−270^\circ$を消したい)とき、
すると、
C(cos)
に移るので
となります。
例:cos から sin に変換(−270°)
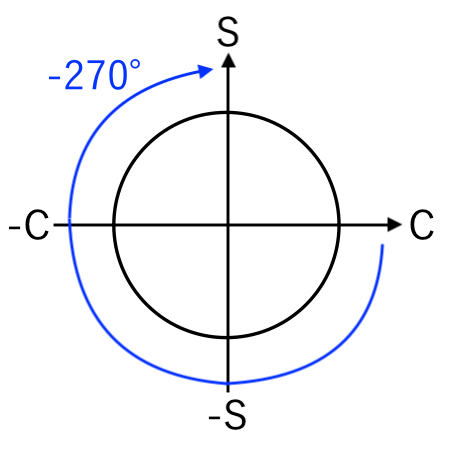
$\cos($ $\theta + 270^\circ$ $)$
$=$ $\theta$
$「 $$\theta + 270^\circ$$ 」$ を $「 $$\theta$$」$にしたい($+270^\circ$を消したい)とき、
すると、
S(sin)
に移るので
となります。
その他の例(270°回転)
以下の計算も同様です。自由自在に変換OK!
$-\sin($ $\theta + 270^\circ$$)$ $= \cos\theta$
・・・「−S」から $-270^\circ$回転 →「C」
$-\cos($ $\theta − 270^\circ$$)$ $= \sin\theta$
・・・「−C」から $+270^\circ$回転 →「S」
$-\cos($ $\theta + 270^\circ$$)$ $= -\sin\theta$
・・・「−C」から $-270^\circ$回転 →「−S」
$\sin$ $310^\circ$ $= -\cos 40^\circ$
・・・「S」から $-270^\circ$回転 →「−C」
$\cos$ $(-250^\circ)$ $= -\sin 20^\circ$
・・・「C」から $+270^\circ$回転 →「−S」
$\sin($ $\theta − 210^\circ$$)$ $= \cos(\theta + 60^\circ)$
・・・「S」から $+270^\circ$回転 →「C」
だいぶ慣れてきましたか?
【練習問題】sin と cos の変換
sin と cos 変換の裏ワザ を実際に使って、問題演習をしてみましょう。
まずは、下のような図を紙に描いておきます。
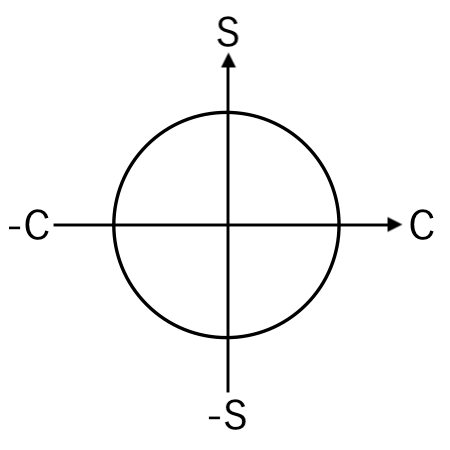
問題は全部で15問。
最後まで解いてから答え合わせしましょう。
準備できたらスタート!
問題
(1) $\sin130^\circ =$ $\cos$
(2) $\cos10^\circ =$ $\sin$
(3) $-\sin(-35^\circ) =$ $\cos$
(4) $\sin(-120^\circ) =$ $-\sin$
(5) $-\cos225^\circ =$ $\cos$
(6) $\sin20^\circ =$ $110^\circ$
(7) $\cos140^\circ =$ $50^\circ$
(8) $\cos(-200^\circ) =$ $70^\circ$
(9) $\sin210^\circ =$ $30^\circ$
(10) $-\sin315^\circ =$ $45^\circ$
(11) $\sin(\theta – 90^\circ) =$ $\theta$
(12) $\cos(90^\circ +\theta ) =$ $\theta$
(13) $-\cos(\theta – 180^\circ) =$ $\theta$
(14) $\cos(270^\circ +\theta) =$ $\theta$
(15) $-\sin(\theta – 270^\circ) =$ $\theta$
解答
- 【解答】を見る
- 【解答】
(1) $\sin130^\circ =$ $\cos$ $40^\circ$
(2) $\cos10^\circ =$ $\sin$ $100^\circ$
(3) $-\sin(-35^\circ) =$ $\cos$ $55^\circ$
(4) $\sin(-120^\circ)=$ $-\sin$ $60^\circ$
(5) $-\cos225^\circ =$ $\cos$ $45^\circ$
(6) $\sin20^\circ =$ $-\cos$ $110^\circ$
(7) $\cos140^\circ =$ $-\sin$ $50^\circ$
(8) $\cos(-200^\circ) =$ $-\sin$ $70^\circ$
(9) $\sin210^\circ =$ $-\sin$ $30^\circ$
(10) $-\sin315^\circ =$ $\cos$ $45^\circ$
(11) $\sin(\theta – 90^\circ) =$ $-\cos$ $\theta$
(12) $\cos(90^\circ +\theta ) =$ $-\sin$ $\theta$
(13) $-\cos(\theta – 180^\circ) =$ $\cos$ $\theta$
(14) $\cos(270^\circ +\theta) =$ $\sin$ $\theta$
(15) $-\sin(\theta – 270^\circ) =$ $-\cos$ $\theta$
【まとめ】sin と cos の変換「裏ワザ」
最後に、sinとcosの変換 を一瞬でやる「裏ワザ」をまとめておきます。

【軸】
- 横軸:C(cos)
- 縦軸:S(sin)
【角度の回転】
- 反時計回り(左回り) → プラス
- 時計回り(右回り) → マイナス
何度も練習して、バッチリ使いこなせるようにしましょう!
質問・要望があれば気軽にコメントください👍
【数学Ⅲ】sinとcosの微分・積分「裏ワザ」
実は、数学Ⅲ「sinとcosの微分・積分」にもこの「裏ワザ」が使えます。
三角関数のsinとcosの微分・積分公式がややこしいな〜 符号がプラスかマイナスかいつも混乱しちゃう・・・ 微積公式を暗記せずに簡単に計算する方法はないの? こんなお悩みを解消します。 この記事を読め[…]