対偶を使った証明がよくわからない
対偶と背理法の違い・使い分けがわからない
対偶と背理法の見分け方を教えてほしい
こんな悩みがあるのなら、今回の記事が役に立つと思います。
元の命題がそのまま証明しにくいときには、対偶 か 背理法 のどちらかで証明すると良いのはご存知ですよね?
背理法 については下の記事で解説しています。
今回の記事は、次のような疑問を持っている人のために書きました。 背理法の使い方・考え方がいまいち分からない 背理法をいつ、どんな問題で使えばいいの? そもそも背理法って何? 正直、意味不明だ・・・ 元の命題がそのまま証明しに[…]
今回は 対偶 の使い方をわかりやすく解説します。
対偶(たいぐう)を利用した証明
対偶とは、簡単に言えば「裏の逆」です。
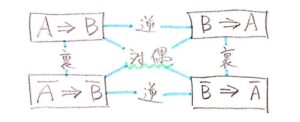
元の命題「A ⇒ B」とすると、
裏「Aでない ⇒ Bでない」なので、さらに逆(矢印を逆にする)にすると
対偶「Bでない ⇒ Aでない」
になります。
そして、対偶の真or偽 = 元の命題の真or偽 というのがポイントです。
つまり、
対偶が 真 なら 元の命題も 真
対偶が 偽 なら 元の命題も 偽
ということです。
対偶をどんな証明で利用すればいいのか?背理法との違いは?
対偶 を利用する問題の特徴
対偶 を使うべき証明問題には「ならば」(⇒)という言葉があります。
例えばこんな問題です。
直接的な証明が難しく、「ならば」も入っているので、対偶を使って証明するのがいい と判断できます。
背理法 を使うべき問題の特徴
一方、背理法 を使うべき証明問題は
のように、「ならば」の言葉がありません。
あとは「でない」、「少なくとも1つ」などの言葉が入っているのも、背理法を使うべき問題の特徴です。
今回の記事は、次のような疑問を持っている人のために書きました。 背理法の使い方・考え方がいまいち分からない 背理法をいつ、どんな問題で使えばいいの? そもそも背理法って何? 正直、意味不明だ・・・ 元の命題がそのまま証明しに[…]
それでは実際に、対偶を使った証明を見ていきましょう。
【例題】整数 a, bについて、ab が 4で割り切れないならば、a, b の少なくとも一方は奇数であることを証明せよ。
これをそのまま証明することは難しいので、対偶か背理法を使おうと考えます。
「ならば」の言葉が入っていて、「少なくとも一方」と書いてあるので 対偶 を使うべきだと判断します。
まず、元の命題「A ⇒ B」を 対偶「Bでない ⇒ Aでない」に書き換えます。
【証明】
対偶「$a, b$ がともに偶数 ならば、$ab$ は 4で割り切れる」を示せばよい。
「$a, b$ の少なくとも一方が奇数」の否定は「$a, b$ がともに偶数」です。
確率における余事象の考え方に似ていますね。
$a, b$ がともに偶数のとき、
$a = 2m, b = 2n$($m, n$:整数)とおける。
$ab = 2m・2n$
$= 4mn$
これは4で割り切れる。
ゆえに、$a, b$ がともに偶数 ならば、$ab$ は 4で割り切れる。
したがって、与題は示された。 [終]
質問・要望があれば気軽にコメントください👍

