【高校数学】二次関数の平方完成は難しくない【簡単に求めるやり方をわかりやすく解説】

2022年9月25日
数学I

数学I

二次関数の「平方完成」の計算に手間取ったり、しかもミスをよくしてしまう

平方完成を素早く、確実に、簡単に計算する方法を知りたい！

そもそもなぜ平方完成するの？

平方完成はいつ使うの？

今回の記事では、こういった悩み・疑問を解決します。

意外と知られていない平方完成の簡単＆確実な計算方法の紹介や、平方完成をいつ使うのかといった「使いどころ」をしっかり解説します。

1 なぜ平方完成をするのか？
- 1.1 二次関数 $y = a(x − p)^2 + q$
2 平方完成の最速テクニック【簡単に求める方法】
- 2.1 【例題】$−5x^2 + 20x + 6$ を平方完成せよ。
- 2.2 まとめ
3 平方完成を練習しよう！
4 マイナスでくくる平方完成のやり方
5 分数でくくる平方完成のやり方
6 文字（定数）でくくる平方完成のやり方
7 ２次関数のグラフの簡単な書き方（裏ワザ）

なぜ平方完成をするのか？

そもそも平方完成は何のためにするのか？

「平方完成」をする目的はズバリ、

二次関数のグラフの形を明らかにするため

です。

二次関数のグラフの形は、主に3つの要素からなります。

① 上に凸 or 下に凸

② 頂点の座標 $(x, y)$

③ 軸 $x = a$

この3つがわかれば、とりあえずグラフを書くことができ、「二次関数の最大、最小を求める問題」は解くことができます。

二次関数 $y = a(x − p)^2 + q$ を例に、それぞれ説明します。

二次関数 $y = a(x − p)^2 + q$

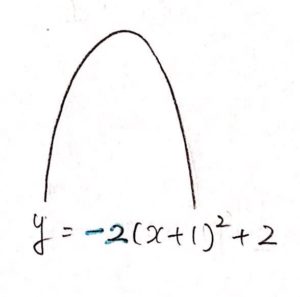
上に凸 or 下に凸

$x^2$ の係数 $a$ の符号を見ます。

プラスなら下に凸です。

逆に、マイナスなら上に凸です。

頂点の座標 $(p, q)$

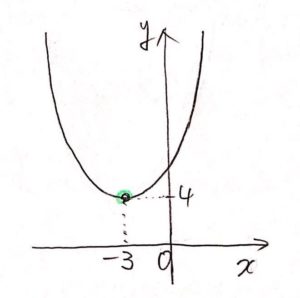
放物線の「頂点」の座標は$(p, q)$になります。

$p$ の符号に気をつけましょう。

$q$はそのままでOKですが、$p$は符号を逆にして書きます。

【例】 $y = 2(x$ $+ 3$$)^2 + 4$ の頂点は $($$−3$$, 4)$

軸 $x = p$

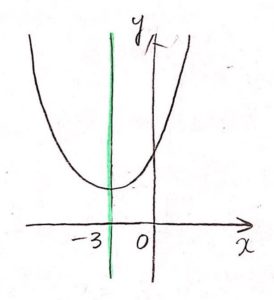
放物線を左右対称に分ける直線を「軸」と言います。

$x = p$ のような形で、$xy$座標平面では 縦にまっすぐのびた直線になります。

【例】 $y = 2(x$ $+ 3$$)^2 + 4$ の軸は $x =$ $−3$

平方完成の最速テクニック【簡単に求める方法】

それでは、平方完成を「素早く」「正確に」「簡単に」やる方法を紹介します。

【例題】$−5x^2 + 20x + 6$ を平方完成せよ。

① $x^2$ の係数（−5）で、前の2項をくくる

$ $ $\color{blue} {−5} x^2 + 20x $ $+ 6$

$=$ $\color{blue} {−5} (x^2 −4x) $ $+ 6$

② 次のように書き換える

$x^2$ → $x$

赤 ÷ 2

$x$ → 消す

括弧を2乗にする

$= −5$$(x^2 − \color{red} {4} x)$ $+ 6$

$= −5$$(x − \color{red} {2} )^2$ ・・・

③ その後ろに「−（赤色の2乗）×（係数）」を書く

$= \color{blue} {−5} (x − \color{red} {2} )^2 $ $− \color{red} {2}^2 \cdot ( \color{blue} {−5})$ ・・・

ひく2乗かける係数

と覚える！（ここがポイント）

2² を計算して 4 と書いてしまうのが早くておすすめ（下の【解答】を参照）。

④ 残りの項を書く

$= −5(x − 2)^2 −2^2 \cdot (−5) $ $+ 6$

⑤ 計算しておわり

$= −5(x − 2)^2 + 26$

一連の流れでやると、下のような計算になります。

【◎計算】

$−5x^2 + 20x + 6$

$= −5(x^2 − 4x) + 6$

$= −5(x − 2)^2 −4 \cdot (−5)+ 6$

$= −5(x − 2)^2 + 26$

教科書に載っているようなやり方と比べてみましょう。

【△計算】

$−5x^2 + 20x + 6$

$= −5(x^2 − 4x) + 6$

$= −5\{(x − 2)^2 −2^2\} + 6$　← 時間ロス！

$= −5\{(x − 2)^2 −4\} + 6$　← 時間ロス！

$= −5(x − 2)^2 +(−5) \cdot (−4) + 6$

$= −5(x − 2)^2 + 26$

まとめ

平方完成の計算に使った行数を見ると「◎計算」は3行、「△計算」は5行です。

つまり、今回紹介した「◎計算」は、教科書に載っている「△計算」と比べると 2行ぶん早く済みます。

まず2行減ることで早く終わるし、書き間違いによる計算ミスも減ります。

さらに慣れてきて、2行目を飛ばせるようになるともっとスピードアップできますね。

上の例で言うと、$\color{green} {-5}x^2 \color{red} {+20}x + 6$ を見たときに「$\color{red} {+20}$ を係数（$\color{green} {-5}$）でくくったら $\color{red} {-4}$、それを$2$で割って $\color{red} {-2}$ だな」と考えながら、$\color{green} {-5}(x\color{red} {-2})^2$・・・と書いていく流れです。（ただし計算・符号ミスには注意！）

そこまで出来るようになると計算がかなり早くなるので、どんどん練習してしっかりマスターしてください！

このように、限られた時間（日々の勉強もテストの時間も）のなかで賢くショートカットするテクニックを身につけましょう。