【２次関数】頂点の座標が分数のグラフの書き方【見やすく書くコツを伝授】(裏ワザあり)

２次関数の頂点の座標が分数のとき、グラフはどうやって書けばいいの？

放物線の頂点が整数の場合、例えば3だったら素直に右に3マス進めばいいけど、分数の場合はどうなるの？

こういった疑問に答えます。

２次関数で「頂点の座標が分数になる」とき、例えば

$ $　$ \displaystyle { y = \left( x + {5 \over 2} \right)^2 − {13 \over 4} } $

みたいなグラフの書き方が、分からなくなるときってありますよね？

２次関数で頂点が分数になるようなグラフの書き方には、いくつかコツがあります。

今回は、

• ２次関数で頂点の座標が 分数 のグラフの書き方（6ステップ）
• もっと放物線を見やすく書くコツ（裏ワザ）

を伝授します。

【２次関数】頂点が分数のグラフの書き方【6ステップ】

「２次関数の頂点の座標が 分数 になるグラフの書き方」を説明します。

ポイントは、ステップ5で「原点$\color{red}{O}$からの距離の 比 を利用すること」です。

詳細は後述します。

この6ステップにしたがって、「頂点の座標が 分数 の２次関数」のグラフを一緒に書いてみましょう！

【ステップ1】平方完成する

まずは 平方完成 して「$y = a(x−p)^2 + q$」の形にします。

「２次関数の平方完成のやり方」をおさらいしたい人はこちら。

関連記事

【高校数学】二次関数の平方完成は難しくない【簡単に求めるやり方をわかりやすく解説】

二次関数の「平方完成」の計算に手間取ったり、しかもミスをよくしてしまう 平方完成を素早く、確実に、簡単に計算する方法を知りたい！ そもそもなぜ平方完成するの？ 平方完成はいつ使うの？ 今回の記事では、こういった悩み・疑問[…]

【ステップ2】頂点、軸、上or下に凸 を求める

ステップ1で平方完成すると

「頂点」「軸」「上or下に凸」

が分かりますね。

【ステップ3】$y$切片を求める

$\color{red}{y}$切片 とは「$y$軸との交点の $y$座標」つまり「$x = 0$ となる $y$の値」です。

よって、「$y$切片は $3$」と分かります。

【ステップ4】$x$軸、$y$軸、原点$O$を書く

$x$軸、$y$軸、原点$O$を書いて、$xy$平面を用意します。

ここまではいつもと同じ流れですね。

【ステップ5】頂点、$y$切片の点を書く

ここからがいよいよ本題です。

まず「頂点の $x$座標」「頂点の $y$座標」「$y$切片」

の3つについて「原点$\color{red}{O}$からの距離」を比較します。

分数の大きさを比べるときは、分母をそろえるんでしたね。

$ \begin{cases}
頂点の x座標：\displaystyle { −{5 \over 2} = − { \color{red}{10} \over 4}} \\
\\
頂点の y座標：\displaystyle { − { \color{red}{13} \over 4} } \\
\\
y切片：\displaystyle { 3 = { \color{red}{12} \over 4} } \\
\end{cases}$

この 比 （$10：13：12$）をもとに「頂点」と「$\color{red}{y}$切片」のだいたいの位置を書き込みます。

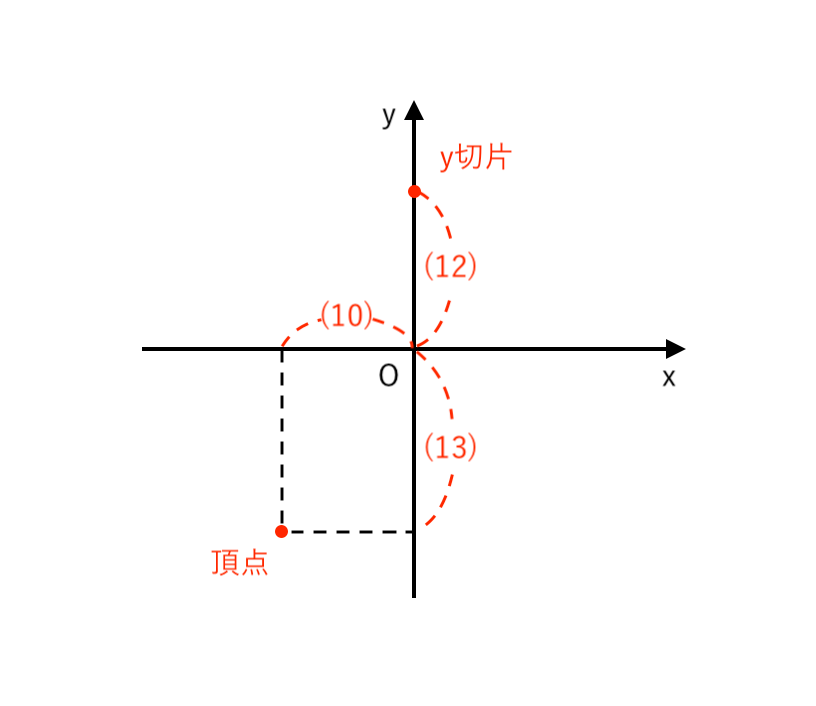
【ステップ6】放物線を書く

ステップ5で書き込んだ「頂点」と「$\color{red}{y}$切片」を通るような放物線をひきます。

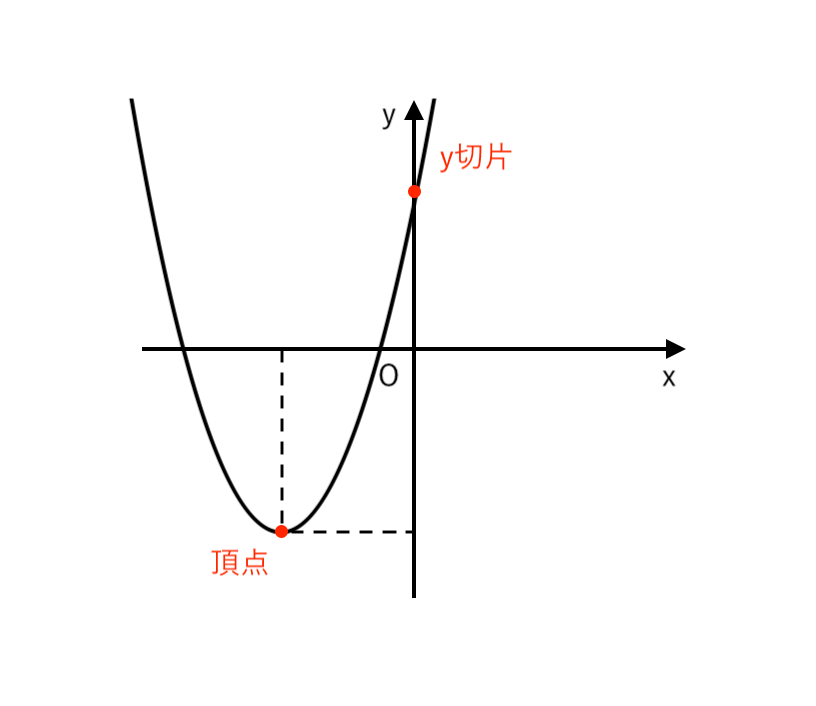
仕上げに「頂点の座標」「$y$切片」の値を書いたら完成です！

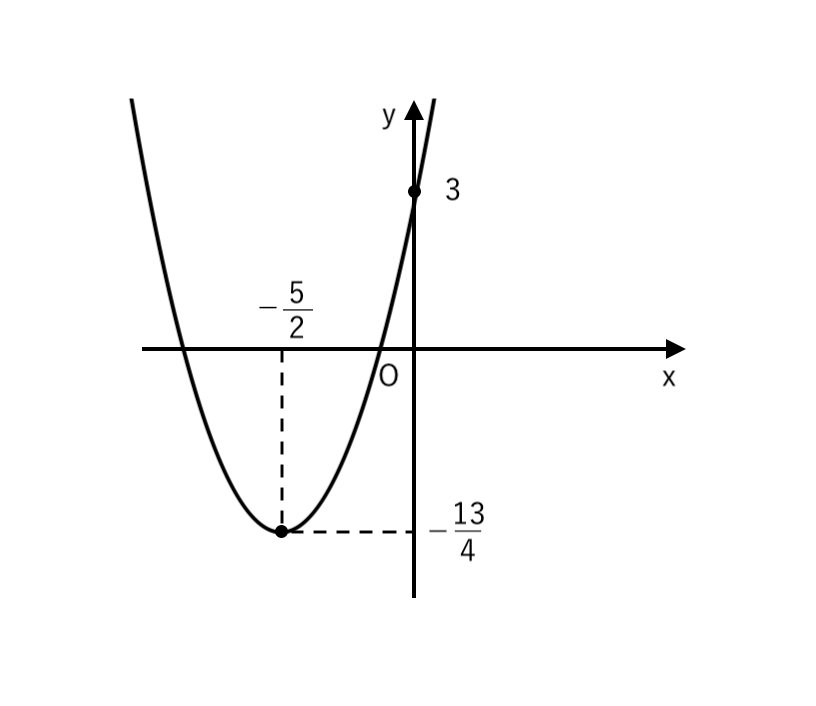
どうでしたか？

分数のまま考えるのではなく、原点$\color{red}{O}$からの距離の「比」で考えるといつもよりグラフが書きやすかったと思います。

【裏ワザ】放物線をもっとキレイに書きたい人へ

上で説明したのは、いわゆる「正攻法（王道）」に比を利用する工夫を加えたやり方です。

ただ、どうしてもこのやり方だと、ステップ6「放物線を書く」ときに 美術センス が大いに問われてしまいます。

そこで紹介したいのが、「誰でも簡単に ２次関数のグラフ が見やすく書ける方法（裏ワザ）」です。

前半（ステップ1〜3）は正攻法と同じですが、

後半（ステップ4〜6）は  いつもと 逆 の順番 でやります。

先ほどの ２次関数 $ y = x^2 + 5x +3 $ のグラフを、「裏ワザ」を使ってもっとキレイに見やすく書いてみましょう！

ステップ1〜3までで以下のことが分かっている状態からスタートです。

$ \begin{cases}
頂点 \enspace \displaystyle { \left( −{5 \over 2} , − {13 \over 4} \right) } \\
\\
下に凸 \\
\\
y切片：3 \\
\end{cases}$

【ステップ4】放物線を書く

ここからが いつもと逆のやり方 です。

書きたいグラフが「上に凸」か「下に凸」か を確認したら、

放物線をとりあえず書いておきます。

【ステップ5】$y$軸を書く

「頂点」と「$\color{red}{y}$切片」の位置を考えながら、

「$y$軸」を書きます。

２次関数 $ \displaystyle { y = \left(x + {5 \over 2} \right)^2 − {13 \over 4} } $ の場合、

• 頂点 $\displaystyle { \left( −{5 \over 2} , − {13 \over 4} \right) }$
• $y$切片：$3$　→　点$(0, 3)$ を通る

ということを考慮すると

$y$軸は、だいたいこの辺り。

もうちょっと細かく説明すると

たて：よこ $ = \displaystyle { \left\{ 3−\left( −{ 13 \over 4 } \right) \right\}：{5 \over 2} = { 25 \over 4 }：{5 \over 2} } $

$ $　　　　　$=$ ⑤：②  くらいの比率になっていればPerfect！

（あまりこだわらなくてもOK）

【ステップ6】$x$軸を書く

最後に「$x$軸」を書きます。

ポイントとしては、

$ $　「$\color{red}{y}$切片」と「頂点の $\color{red}{y}$座標」

のバランスを考えて $x$軸 の位置を決定するとGood！

今回の場合、

• $y$切片：$3$
• 頂点の $y$座標：$\displaystyle { − { 13 \over 4} }$

この2点の真ん中（中点の $y$座標）は

$ $　$\displaystyle { { 1 \over 2 } \left( 3−{ 13 \over 4 } \right) = \color{red}{−{ 1 \over 8 } } }$

なので、それよりちょっと上あたりに $x$軸（直線 $y = 0$）をひきます。

仕上げに「原点$O$」や「頂点の座標」などを書き込んだら、グラフの完成です！

いかがでしたか？ いつもより キレイで見やすいグラフ が書けたと思いませんか？

なお、「たて：よこ」の比率は問題を解く上ではさほど重要ではないので、あまり気にしなくても大丈夫です。

慣れるまでは大変かもしれませんが、見やすいグラフが書けると 確実に ２次関数 の問題が解きやすくなります。

ぜひ練習してマスターしてみてください！

【練習問題】２次関数の頂点が分数のグラフ

ここまでで学んだやり方を使って「２次関数で頂点の座標が 分数 のグラフ」を書く練習をしてみましょう！

正攻法と裏ワザ、どっちで書いてもOKです！

【解答】を見る

【解答】

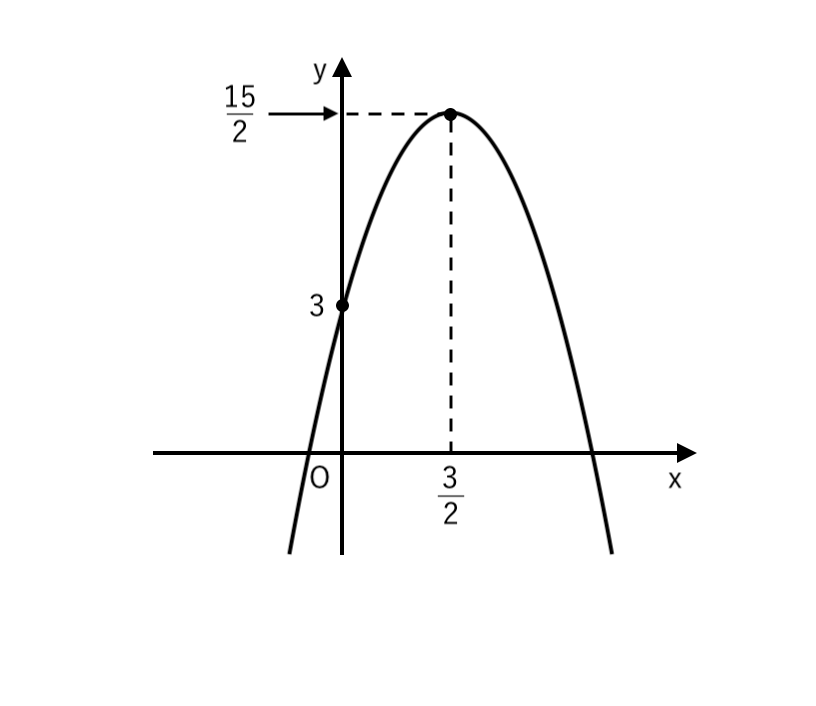
(1)

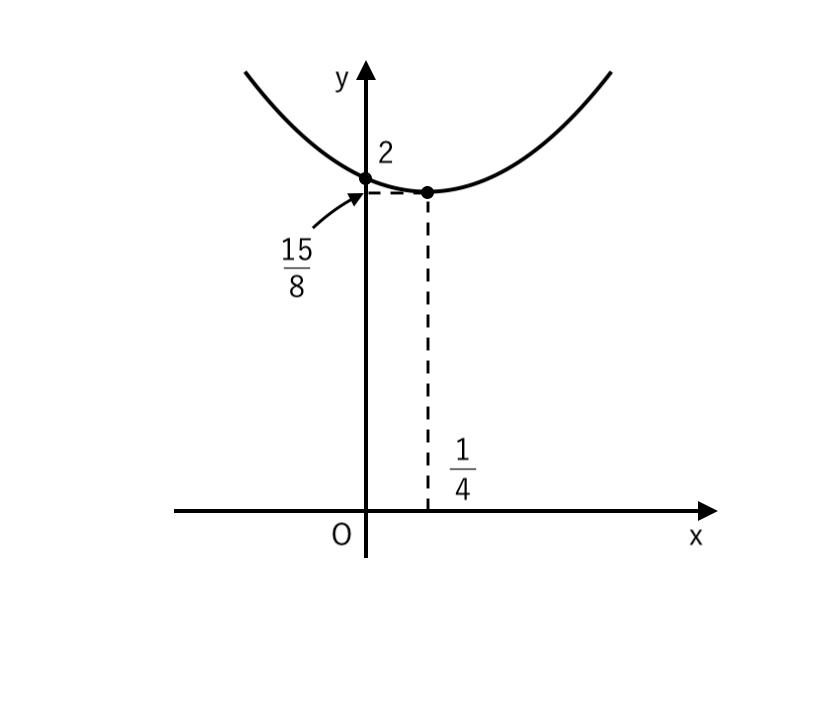
(2)

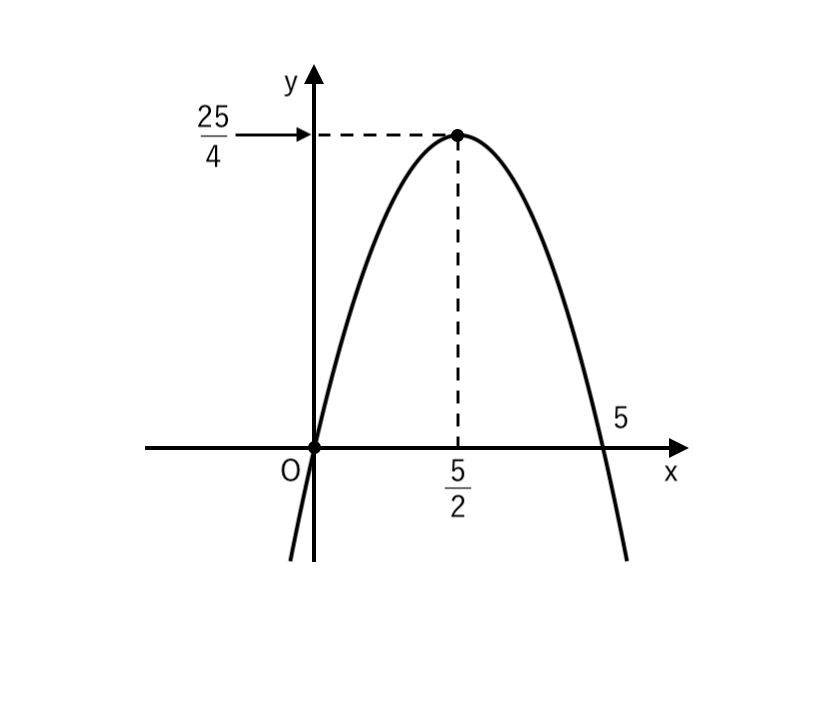
(3)

グラフを書くまでの過程（解説）はこちら。

【解説】を見る

【解説】

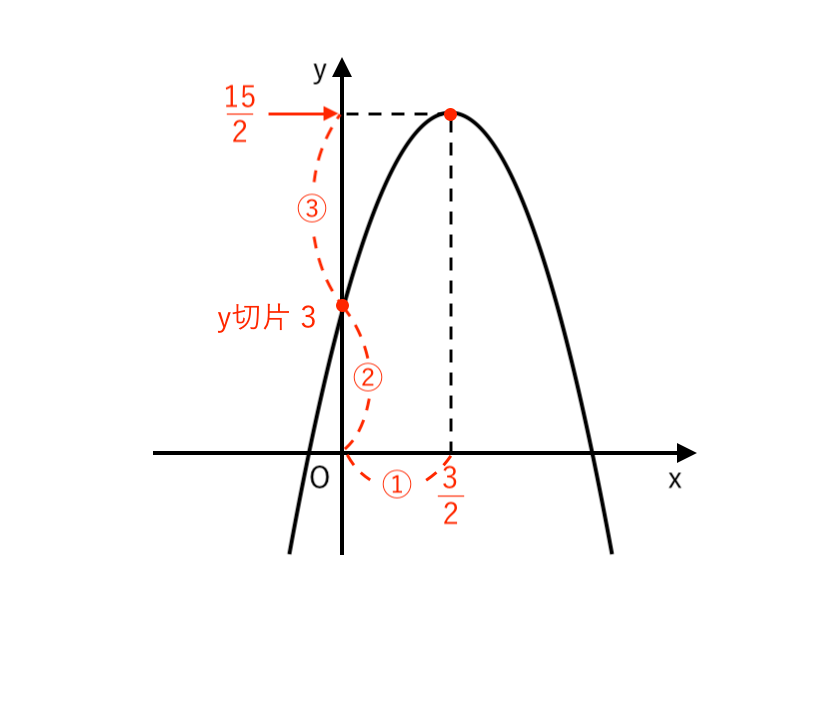
(1) $ y = −2 x^2 + 6 x + 3 $

$ $　　$ = −2 \left( x^2 − 3 x \right) + 3 $

$ $　　$\displaystyle { = −2 \left( x − {3 \over 2} \right)^2 −{9 \over 4} \cdot (−2) + 3 } $

$ $　　$\displaystyle { = −2 \left( x − {3 \over 2} \right)^2 + {15 \over 2} } $

∴ $ \begin{cases}
\displaystyle { 頂点 \enspace \left( {3 \over 2} , {15 \over 2} \right) } \\
\\
\displaystyle { 軸：x = {3 \over 2} }   \\
\\
上に凸 \\
\end{cases}$　の放物線

また、$x = 0$ のとき　$ y = 3 $

∴ $y$切片：$3$

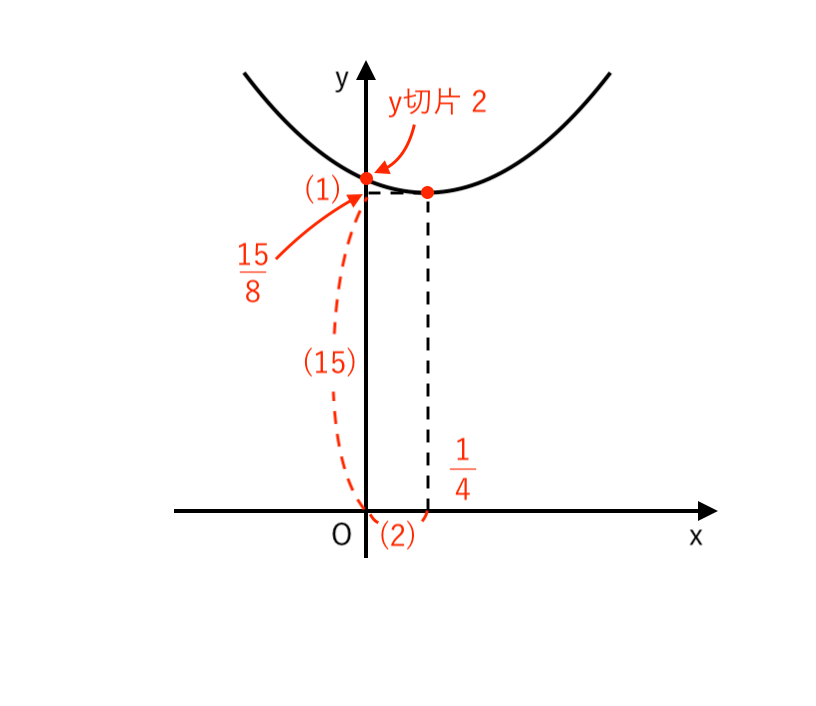
(2) $ y = 2 x^2 − x + 2 $

$ $　　$ \displaystyle { = 2 \left(x^2 − {1 \over 2}x \right) + 2 } $

$ $　　$ \displaystyle { = 2 \left(x − {1 \over 4} \right)^2 − {1 \over 16} \cdot 2 + 2 } $

$ $　　$ \displaystyle { = 2 \left(x − {1 \over 4} \right)^2 + {15 \over 8} } $

∴ $ \begin{cases}
\displaystyle { 頂点 \enspace \left( {1 \over 4} , {15 \over 8} \right) } \\
\\
\displaystyle { 軸：x = {1 \over 4} }   \\
\\
下に凸 \\
\end{cases}$　の放物線

また、$x = 0$ のとき　$ y = 2 $

∴ $y$切片：$2$

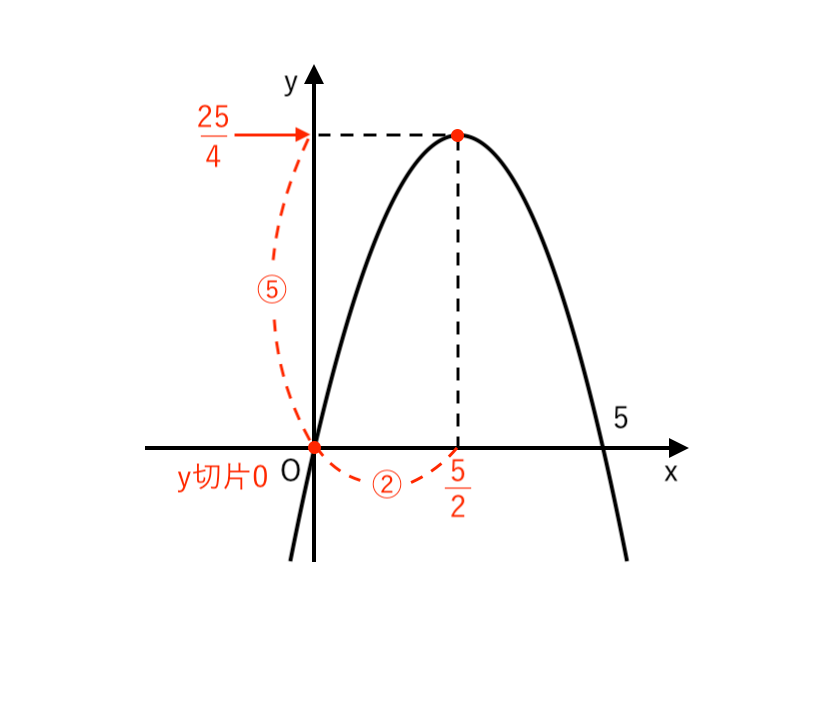
(3) $ y = −x^2 + 5 x $

$ $　　$ \displaystyle { = − \left(x^2 − 5 x \right) } $

$ $　　$ \displaystyle { = − \left(x − {5 \over 2} \right)^2 −{25 \over 4} \cdot (−1) } $

$ $　　$ \displaystyle { = − \left(x − {5 \over 2} \right)^2 + {25 \over 4} } $

∴ $ \begin{cases}
\displaystyle { 頂点 \enspace \left( {5 \over 2} , {25 \over 4} \right) } \\
\\
\displaystyle { 軸：x = {5 \over 2} }   \\
\\
上に凸 \\
\end{cases}$　の放物線

また、$x = 0$ のとき　$ y = 0 $

∴ $y$切片：$0$　→　原点$O$ を通る

【まとめ】２次関数の頂点が分数のグラフの書き方

今回は「２次関数で頂点の座標が 分数 のグラフの書き方」を紹介しました。

ポイントは、ステップ5で「原点$\color{red}{O}$からの距離の 比 を利用すること」でしたね。

たくさん練習してグラフの書き方に慣れておきましょう！

質問・要望があれば気軽にコメントください👍

参考：２次関数のグラフの簡単な書き方【裏ワザ】

今回紹介した「裏ワザ」をもっと学びたい人はこちら。

関連記事

【高校数学】２次関数のグラフの簡単な書き方【放物線をキレイに見やすく書く裏ワザ】

２次関数のグラフ（放物線）がフリーハンドでうまく書けない・・・ 放物線をキレイに見やすく書くのって難しいな〜 ２次関数のグラフの簡単な書き方・裏ワザを教えてほしい！ こういった要望に応えます。   実は「[…]