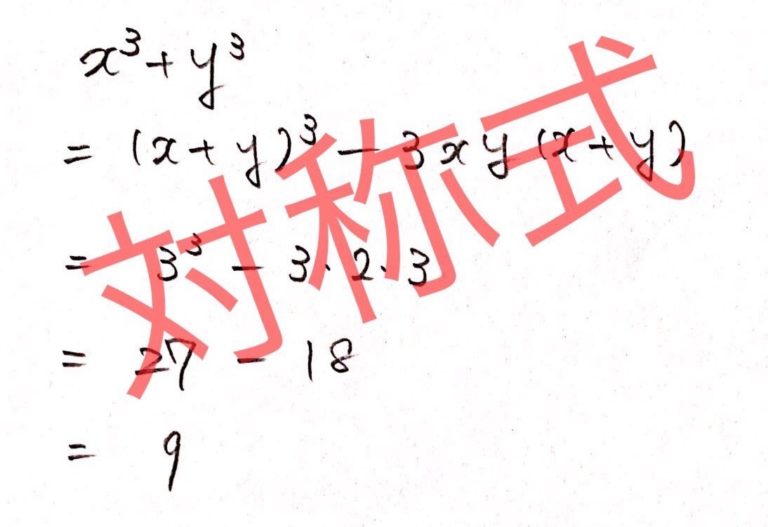【高校数学】対称式（交代式）の解き方をわかりやすく解説【基本定理はこれだけ覚えよう】

2022年10月23日
数学I

数学I

対称式・交代式の解き方がよくわからない

そもそも対称式って何？

対称式のわかりやすい解説が聞きたい！

今回はこういった疑問・要望にお答えします。

対称式（交代式）の問題は、解法が完全にパターン化されています（やり方が決まっている）。

このページを読み終えた頃には、対称式の問題が出ても楽勝で解けるようになっているはずです。

1 対称式（交代式）とは【基本からおさらい】
- 1.1 対称式とは？
- 1.2 交代式とは？
2 対称式（交代式）の解き方・考え方
3 【例題1】x + y = 3, xy = 2 のとき、x² + y², x³ + y³ の値をそれぞれ求めよ。
4 【例題2】 x = √5 + √3, y = √5 − √3 のとき、x² + y², x⁴ + y⁴ , x⁵ + y⁵ の値を求めよ。
5 分数を含む対称式（交代式）の解き方
6 3変数の対称式（交代式）の解き方
7 参考：対称式×三角比【応用問題】

対称式（交代式）とは【基本からおさらい】

対称式

対称式とは？

対称式とは「文字を入れ替えても同じ形になる式」のことです。

もしピンと来なければ、点対称や線対称を思い出してください。

点対称は「点について入れ替えても同じ形になる」、線対称は「直線について入れ替えても同じ形になる」図形ですよね？

それと同様のイメージです。

例： $x^2 + 5xy + y^2$

$x, y$ を入れ替えても

$y^2 + 5yx + x^2$

$= x^2 + 5xy + y^2$

となり、元の形と一緒ですね。

こういった式を 対称式と言います。

交代式とは？

一方、交代式とは「文字を入れ替えると符号が交代する式」のこと。

例： $x − y$、$x^2 − y^2$

$x − y$ の文字 $x, y$ を入れ替えると

$y − x$

$= −x + y$

となり、元の形と符号が逆（交代）になっていますね。

こういった式を 交代式と言います。

対称式（交代式）の解き方・考え方

対称式（交代式）の解き方を解説していきます。

まず次のことをおさえてください。

対称式は和（$x +y$）と積（$xy$）で表すことができる

先ほどの例で言えば、

$x^2 + 5xy + y^2$

$= (x + y)^2 + 3xy$

$=$ 和$^2 + 3×$積

のように、和$（$ $x +y$ $）$と積$（$ $xy$ $）$で表せます（基本対称式といいます）。

この性質を利用して、対称式の問題を解いていきます。

【例題1】x + y = 3, xy = 2 のとき、x² + y², x³ + y³ の値をそれぞれ求めよ。

この問題を解く前に、次の公式をしっかり覚えておきましょう。

$x^2 + y^2 = (x + y)^2 − 2xy$
$x^3 + y^3 = (x + y)^3 − 3xy(x + y)$

それぞれ証明しておきます。

① の証明

$(x + y)^2 = \color{red} {x^2} + 2xy + \color{red} {y^2}$

$∴ \color{red} {x^2} + \color{red} {y^2} = (x + y)^2 − 2xy$

② の証明

$(x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3$

∴ $(x + y)^3 = \color{red} {x^3} + 3xy(x + y) + \color{red} {y^3}$

$∴ \color{red} {x^3} + \color{red} {y^3} = (x + y)^3 − 3xy(x + y)$

これらの 対称式の公式 を使って解いていきましょう。

【解答】を見る: 【解答】

$x^2 + y^2$

$= (x + y)^2 − 2xy$

$= 3^2 − 2 \cdot 2$

$= 9 − 4$

$= 5$

$x^3 + y^3$

$= (x + y)^3 − 3xy(x + y)$

$= 3^3 − 3 \cdot 2 \cdot 3$

$= 27 − 18$

$= 9$

別解として、「対称式の公式」を使わず、$ x + y = 3$ （和）の式を「2乗、3乗する」やり方もあります。

【別解1】を見る: 【別解1】

$ $　$ x + y = 3 $

の両辺を2乗して

$ $　$ ( x + y )^2 = 3^2 $

$ $　∴ $ x^2 +2 x y + y^2 = 9 $

ここに $xy = 2$ を代入して

$ $　$ x^2 +2 \cdot 2 + y^2 = 9 $

$ $　∴ $ x^2 + y^2 = 5 $

また

$ $　$ x + y = 3 $

の両辺を3乗して

$ $　$ ( x + y )^3 = 3^3 $

$ $　∴ $ x^3 +3x^2y +3xy^2 + y^3 = 3^3 $

$ $　∴ $ x^3 + y^3 +3x^2y +3xy^2 = 27 $

$ $　∴ $ x^3 + y^3 + 3xy (x + y) = 27 $

ここに $ x + y =3, xy = 2 $ を代入して

$ $　$ x^3 + y^3 + 3 \cdot 2 \cdot 3 = 27 $

$ $　∴ $ x^3 + y^3 = 9 $

もうひとつ別解として、$x^3 + y^3$ は 因数分解の公式 を使って解くこともできます。

$ x^3 + y^3 = (x+y) (x^2 −xy +y^2) $

【別解2】を見る: 【別解2】

$x^3 + y^3$

$= (x + y)( \color{red} {x^2} −xy + \color{red} {y^2} )$

$= 3( \color{red} {5} − 2)$

$= 9$

このように色んな解法を使えるようになっておくと、応用が効くようになってオススメです！

【例題2】 x = √5 + √3, y = √5 − √3 のとき、x² + y², x⁴ + y⁴ , x⁵ + y⁵ の値を求めよ。

(0) 基本対称式

対称式の問題 では、はじめに2つの「基本対称式」

$ $　和$（$ $x +y$ $）$と積$（$ $xy$ $）$

を求めておくのがポイントです。

【解答】

$x + y = 2\sqrt{5}, \, xy = 2$ ・・・①

(1) x² + y²

「対称式の公式（2乗）」をそのまま使います。

$x^2 + y^2 = (x + y)^2 − 2xy$

【解答】

$x^2 + y^2$

$= (x + y)^2 − 2xy$

$= \left(2\sqrt{5} \right)^2 − 2 \cdot 2$　（①より）

$= 20 − 4$

$= 16$ ・・・②

(2) x⁴ + y⁴

「4乗＝ (2乗)$^2$」で作れますね。

【解答】

$x^4+ y^4$

$= \left(x^2 \right)^2 + \left(y^2 \right)^2$

$= A^2 + B^2$　（$A = x^2, B = y^2$ とおく）

$= (A + B)^2 − 2AB$

$= \left(x^2 + y^2 \right)^2 − 2x^2y^2$　（$A, B$ を元に戻す）

$= \left(x^2 + y^2 \right)^2 − 2(xy)^2$

$= 16^2 − 2 \cdot 2^2$　（①、②より）

$= 256 − 8$

$= 248$

(3) x⁵ + y⁵

5乗ってどうやって作るの？と考えると

「5乗＝ 2乗 × 3乗」で作れそうですね。

$ $　$ x^5 + y^5 = \left( x^2 + y^2 \right) \left( x^3 + y^3 \right) − x^3 y^2 −x^2 y^3 $

$ $　　　　$ = \left( x^2 + y^2 \right) \left( x^3 + y^3 \right) −x^2 y^2 \left( x + y \right)$

これは「対称式の公式（5乗）」として覚えておきましょう。

$ x^5 + y^5 = \left( x^2 + y^2 \right) \left( x^3 + y^3 \right) −x^2 y^2 ( x + y )$

というわけで、まずは $ x^3 + y^3 $ を求める必要がありますね。

$x^3 + y^3 = (x + y)^3 − 3xy(x + y)$

【解答】

$ x^3 + y^3 $

$ = (x + y)^3 − 3xy(x + y) $

$ = \left( 2\sqrt{5} \right)^3 − 3 \cdot 2 \cdot 2\sqrt{5} $　（①より）

$ = 40 \sqrt{5} − 12 \sqrt{5} $

$ = 28 \sqrt{5} $・・・③

$ x^5 + y^5 $

$ = \left( x^2 + y^2 \right) \left( x^3 + y^3 \right) −x^2 y^2 ( x + y )$

$ = 16 \cdot 28 \sqrt{5} −2^2 \cdot 2\sqrt{5} $　（①、②、③より）

$ = 448 \sqrt{5} −8 \sqrt{5} $

$ = 440 \sqrt{5} $

まとめ

ここまでの「対称式の公式」を使った解答をまとめます。

【解答】を見る: 【解答】

$x + y = 2\sqrt{5}$, $xy = 2$ ・・・①

$x^2 + y^2$

$= (x + y)^2 − 2xy$

$= \left(2\sqrt{5} \right)^2 − 2 \cdot 2$　（①より）

$= 20 − 4$

$= 16$ ・・・②

$x^4+ y^4$

$= \left(x^2 \right)^2 + \left(y^2 \right)^2$

$= A^2 + B^2$　（$A = x^2, B = y^2$ とおく）

$= (A + B)^2 − 2AB$

$= \left(x^2 + y^2 \right)^2 − 2x^2y^2$　（$A, B$ を元に戻す）

$= \left(x^2 + y^2 \right)^2 − 2(xy)^2$

$= 16^2 − 2 \cdot 2^2$　（①、②より）

$= 256 − 8$

$= 248$

$ x^3 + y^3 $

$ = (x + y)^3 − 3xy(x + y) $

$ = \left( 2\sqrt{5} \right)^3 − 3 \cdot 2 \cdot 2\sqrt{5} $　（①より）

$ = 40 \sqrt{5} − 12 \sqrt{5} $

$ = 28 \sqrt{5} $・・・③

$ x^5 + y^5 $

$ = \left( x^2 + y^2 \right) \left( x^3 + y^3 \right) −x^2 y^2 ( x + y )$

$ = 16 \cdot 28 \sqrt{5} −2^2 \cdot 2\sqrt{5} $　（①、②、③より）

$ = 448 \sqrt{5} −8 \sqrt{5} $

$ = 440 \sqrt{5} $

(1)、(2) の別解として「和を2乗する」やり方もあります。

【別解】を見る: 【別解】

$ x + y = 2 \sqrt{5} $ ・・・①

$ xy = 2 $ ・・・②

①の両辺を2乗して

$ $　$ ( x + y )^2 = \left( 2 \sqrt{5} \right)^2 $

$ $　∴ $ x^2 + 2xy + y^2 = 20 $

②を代入して

$ $　$ x^2 + 2 \cdot 2 + y^2 = 20 $

$ $　∴ $ x^2 + y^2 = 16 $ ・・・③

③の両辺を2乗して

$ $　$ \left( x^2 + y^2 \right)^2 = 16^2 $

$A = x^2, B = y^2$ とおくと

$ $　$ ( A + B )^2 = 16^2 $

$ $　∴ $ A^2 + 2AB + B^2 = 256 $

$A, B$ を元に戻すと

$ $　∴ $ \left(x^2 \right)^2 + 2x^2 y^2 + \left(y^2 \right)^2 = 256 $

$ $　∴ $ x^4 + 2 (x y)^2 + y^4 = 256 $

②を代入して

$ $　∴ $ x^4 + 2 \cdot 2^2 + y^4 = 256 $

$ $　∴ $ x^4 + y^4 = 248 $

(3) の別解として「5乗 = 4乗 × 1乗」と考えるやり方もあります。

【別解】を見る: 【別解】

$ x^5 + y^5 $

$ = \left( x^4 + y^4 \right) \left( x + y \right) −xy \, ( x^3 + y^3 )$

$ = 248 \cdot 2 \sqrt{5} −2 \cdot 28 \sqrt{5} $

$ = 496 \sqrt{5} −56 \sqrt{5} $

$ = 440 \sqrt{5} $

以上です。お疲れ様でした！