θが鈍角(90°以上)のときの「三角比の相互関係」の求め方がわからない!
θが鈍角(90°以上)の sin cos tan がイメージできない・・・
単位円の図でわかりやすく解説してほしい!
こういった要望に応えます。
「三角比の相互関係」の公式は3つ。
- $\sin^2 \theta + \cos^2 \theta = 1$
- $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
- $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
「θが鈍角(90°以上)のとき、三角比 sin cos tan をどうやって求めたらいいのか?」
という質問をよくいただくので、今回記事にしてみました。
このページを読めば、θが鈍角(90°以上)のときの「三角比の相互関係」を悩むことなくスムーズに求められるようになります。
なお、「三角比の相互関係」の公式の覚え方についてはこちら。
「三角比の相互関係」の3つの公式が覚えられない! 簡単に暗記したり、証明する方法を知りたい! 「三角比の相互関係」をいつ使うのか、タイミングや問題を教えてほしい! こういった要望に応えます。 「三角比[…]
【三角比の相互関係】θが鈍角(90°以上)のときの求め方
θが鈍角(90°以上)の「三角比の相互関係」の求め方では、
ということがポイントです。
$\theta$ が鈍角 $\displaystyle { \left( 90^\circ<\theta<180^\circ \right) }$ のとき、単位円をかくと
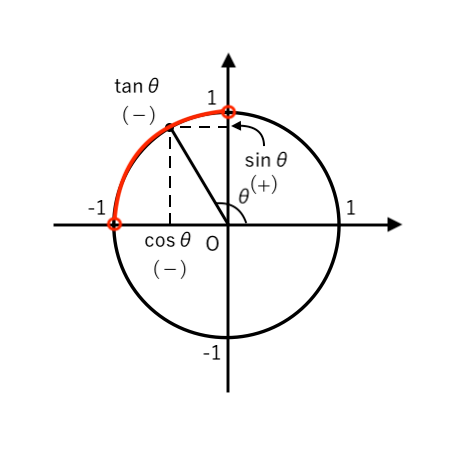
単位円では
- $\cos \theta$:$x$座標(よこ)
- $\sin \theta$:$y$座標(たて)
- $\tan \theta$:直線の 傾き
と考えればOKですよね。
よって
\cos \theta <0(−) \\
\\
\sin \theta >0(+) \\
\\
\tan \theta <0(−) \\
\end{cases}$
となります。
【三角比の相互関係】θが鈍角(90°以上)の問題の解き方
実際に、θが鈍角(90°以上)の問題 を解いてみましょう!
【例題】$\theta$ は鈍角とする。三角比の1つが次の値をとるとき、他の2つの三角比の値を求めよ。
(1) $ \displaystyle { \sin \theta = { 1 \over \sqrt{3} } } $
(2) $ \displaystyle { \tan \theta = − { 2 \over \sqrt{5} } } $
(1) $ \displaystyle { \sin \theta = { 1 \over \sqrt{3} } } $
「三角比の相互関係」の公式をおさらいしましょう。
- $\sin^2 \theta + \cos^2 \theta = 1$
- $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
- $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
この問題を解く手順としては、
【公式①】$\sin \theta $ から $\cos \theta $ を求める
【公式②】$\sin \theta $、$\cos \theta $ から $\tan \theta $ を求める
という流れが一番スムーズです。
もちろん前半で
$ $ 【公式③】$\sin \theta $ から $\tan \theta $ を求める
というのもアリですが、少し計算が面倒なので「公式①」の方がいいですね。
【解答】
$ $ $\sin^2 \theta + \cos^2 \theta = 1$
に $ \displaystyle { \sin \theta = { 1 \over \sqrt{3} } } $ を代入して
$ $ $ \displaystyle { \left( { 1 \over \sqrt{3} } \right)^2 + \cos^2 \theta = 1 } $
$ $ ∴ $\displaystyle { { 1 \over 3 }+ \cos^2 \theta = 1 } $
$ $ ∴ $\displaystyle { \cos^2 \theta = { 2 \over 3 } } $
ここで、$\theta$ は鈍角 $\displaystyle { \left( 90^\circ<\theta<180^\circ \right) }$ より
$ $ $\cos\theta<0$ ・・・(注)
∴ $\displaystyle {\cos\theta = − \sqrt{ 2 \over 3 } }$
$ $ $= \displaystyle { − { \sqrt{6}\over 3 } } $
また、
$ $ $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
$ $ $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$
$ $ $\displaystyle { = { 1 \over \sqrt{3} } \cdot \left( − { 3 \over \sqrt{6} } \right) }$
$ $ $\displaystyle { = − { \require{cancel} \bcancel{ 3 } \over \bcancel{ 3 } \sqrt{2} } }$
$ $ $\displaystyle { = − { 1 \over \sqrt{2} } }$
$ $ $\displaystyle { = − { \sqrt{2} \over 2 } }$
(注)$\theta$ は鈍角 $\displaystyle { \left( 90^\circ <\theta<180^\circ \right) }$ より、$\cos\theta$ の符号を 単位円で確認すると

なので、$\cos\theta<0$ とわかります。
$\cos^2\theta$ の2乗を外すときに「負(マイナス)の平方根」だけOKということですね。
(2) $ \displaystyle { \tan \theta = − { 2 \over \sqrt{5} } } $
まず $ \tan \theta $ の値が与えられているので、
【公式③】$\tan \theta $ から $\cos \theta $ を求める
【公式②】$\tan \theta $、$\cos \theta $ から $\sin \theta $ を求める
という流れが一番ラクですね。
後半は別解もあるので、後述します。
【解答】
$ $ $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
に $ \displaystyle { \tan \theta = − { 2 \over \sqrt{5} } } $ を代入して
$ $ $\displaystyle { 1 + \left( − { 2 \over \sqrt{5} } \right)^2 = {1 \over \cos^2 \theta} } $
$ $ ∴ $\displaystyle { 1 + { 4 \over 5 } = {1 \over \cos^2 \theta} } $
$ $ ∴ $\displaystyle { {1 \over \cos^2 \theta} = { 9 \over 5 } } $
両辺の逆数をとって
$ $ $\displaystyle { \cos^2 \theta = { 5 \over 9 } } $
ここで、$\theta$ は鈍角 $\displaystyle { \left( 90^\circ<\theta<180^\circ \right) }$ より
$ $ $\cos\theta<0$
∴ $\displaystyle {\cos\theta = − \sqrt{ 5 \over 9 } }$
$ $ $= \displaystyle { − { \sqrt{5} \over 3 } } $
また、
$ $ $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$ ・・・(注)
の両辺に $ \cos \theta $ をかけて
$ $ $\displaystyle { \tan \theta \cdot \cos \theta = {\sin \theta \over \require{cancel} \bcancel{ \cos \theta } } \cdot \bcancel{ \cos \theta } }$
左辺と右辺を入れ替えて
$ $ $\displaystyle { \sin \theta = \tan \theta \cdot \cos \theta }$
$ $ $\displaystyle { = − { 2 \over \sqrt{5} } \cdot \left( − { \sqrt{5} \over 3 } \right) }$
$ $ $\displaystyle { = { 2 \over 3 } } $
(注)ここからの別解として、
$ $ 【公式①】$ \cos\theta $ から $ \sin\theta $ を求める
$ $ というのもできますね。
【別解】
$ $ $\sin^2 \theta + \cos^2 \theta = 1$
に $\displaystyle {\cos\theta = − { \sqrt{5} \over 3 } }$ を代入して
$ $ $\displaystyle { \sin^2 \theta + \left( − { \sqrt{5} \over 3 } \right)^2 = 1 } $
$ $ ∴ $\displaystyle { \sin^2 \theta + { 5 \over 9 } = 1 } $
$ $ ∴ $\displaystyle { \sin^2 \theta = { 4 \over 9 } } $
ここで、$\theta$ は鈍角 $\displaystyle { \left( 90^\circ<\theta<180^\circ \right) }$ より
$ $ $\sin\theta>0$・・・(注)
∴ $\displaystyle {\sin\theta = \sqrt{ 4 \over 9 } }$
$ $ $= \displaystyle { 2 \over 3 } $
(注)$\theta$ は鈍角 $\displaystyle { \left( 90^\circ <\theta<180^\circ \right) }$ より、$\sin\theta$ の符号を 単位円で確認すると

なので、$\sin\theta>0$ とわかります。
$\sin^2\theta$ の2乗を外すときに「正(プラス)の平方根」だけOKということですね。
【まとめ】「三角比の相互関係」θが鈍角(90°以上)
θが鈍角(90°以上)の「三角比の相互関係」の求め方のポイントは、
ということ。
$\theta$ が鈍角 $\displaystyle { \left( 90^\circ<\theta<180^\circ \right) }$ のとき、

\cos \theta <0(−) \\
\\
\sin \theta >0(+) \\
\\
\tan \theta <0(−) \\
\end{cases}$
これをチェックしておけば心配ありません!
質問・要望があれば気軽にコメントください👍
「三角比の相互関係」公式なしで簡単に求める「裏ワザ」
「三角比の相互関係」を公式を使わず、一瞬で&簡単に求める「裏ワザ」もあります。
sin cos tanを求めるときに「三角比の相互関係」の公式をいちいち使うのが面倒だ・・・ 「三角比の相互関係」の公式3つを使わずに、サクッと簡単に計算する方法が知りたい! こういった要望に応えます。 […]


