【三角比の相互関係】テスト・入試によくでる応用問題【レベル1〜5】(わかりやすい図＆解説つき)

「三角比の相互関係」を使った応用問題を解いておきたい！

テスト・入試によくでる応用問題はどんなものがあるの？

図を使ってわかりやすく解説してほしい！

こういった要望に応えます。

「三角比の相互関係」の公式は3つ。

これらの公式を使って解く問題は、学校のテスト でも 大学入試 でもよく出題されます。

このページを最後まで読むことで、テストや入試によく出るパターンの 三角比の応用問題 をひと通り学ぶことができます。

「自分は 三角比の頻出パターンをどれくらい理解できているのか？」をチェックする意味でもぜひ活用してください！

たくさん図を使いながら、視覚的にも分かりやすく丁寧に解説していきます！

【三角比の相互関係】テストによくでる応用問題 Lv.0 (三角比の値)

まずは基本問題のおさらいです。

$\theta$ の値のとる範囲 に気をつけながら解いていきましょう。

(1) $ \displaystyle { \cos \theta = { 1 \over \sqrt{3} } } $ $\displaystyle { \left( 0^\circ＜\theta＜90^\circ \right) }$

手順としては、

というのが一番スムーズです。

【解答・解説】を見る

【解答】

$ $　$\sin^2 \theta + \cos^2 \theta = 1$

に $ \displaystyle { \cos \theta = { 1 \over \sqrt{3} } } $ を代入して

$ $　$ \displaystyle { \sin^2 \theta + \left( { 1 \over \sqrt{3} } \right)^2 = 1 } $

$ $　∴ $\displaystyle { \sin^2 \theta + { 1 \over 3 } = 1 } $

$ $　∴ $\displaystyle { \sin^2 \theta = { 2 \over 3 } } $

 

ここで、$\displaystyle { 0^\circ＜\theta＜90^\circ }$ より

$ $　$\sin\theta＞0$ ・・・（注）

∴ $\displaystyle {\sin\theta = \sqrt{ 2 \over 3 } }$

$ $　　　  $= \displaystyle { \sqrt{6} \over 3 } $

 

また、

$ $　$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$

$ $　　　  $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$

$ $　　　  $\displaystyle { = { \sqrt{6} \over 3 } \cdot \sqrt{3} }$

$ $　　　  $\displaystyle { = { \require{cancel} \bcancel{3}  \sqrt{2} \over \bcancel{3} } }$

$ $　　　  $\displaystyle { = \sqrt{2} }$

（注）$0^\circ ＜\theta＜90^\circ$ より、$\sin\theta$ の符号を 単位円で確認すると

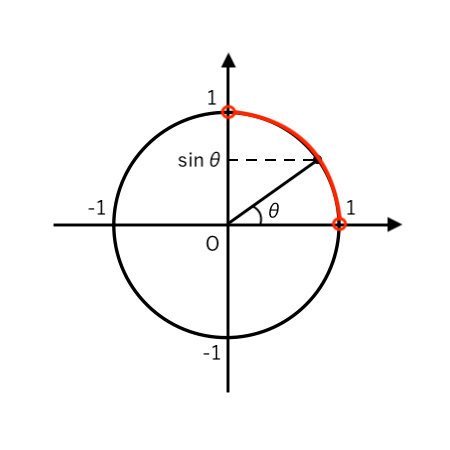
なので、$\sin\theta＞0$（+）とわかります。

$\sin^2\theta$ の2乗を外すときに「正（+）の平方根」だけOKということですね。

(2) $ \displaystyle { \sin \theta = { 2 \over 3 } } $ $\displaystyle { \left( 0^\circ＜\theta＜180^\circ \right) }$

この問題も

というのが良さげですね。

【解答・解説】を見る

【解答】

$ $　$\sin^2 \theta + \cos^2 \theta = 1$

に $ \displaystyle { \sin \theta = { 2 \over 3 } } $ を代入して

$ $　$ \displaystyle { \left( { 2 \over 3 } \right)^2 + \cos^2 \theta = 1 } $

$ $　∴ $\displaystyle { { 4 \over 9 }+ \cos^2 \theta = 1 } $

$ $　∴ $\displaystyle { \cos^2 \theta = { 5 \over 9 } } $

 

ここで、「$0^\circ ＜\theta＜180^\circ$ かつ $\sin \theta＞0$」すなわち

「$0^\circ ＜\theta＜180^\circ$」より

$ $　$\displaystyle {\cos\theta = \pm \sqrt{ 5 \over 9 } }$

$ $　　　  $= \displaystyle { \pm { \sqrt{5}\over 3} } $・・・（注1）

 

また、

$ $　$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$

$ $　　　  $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$

$ $　　　  $\displaystyle { = { 2 \over 3 } \cdot {  \left( \pm { 3 \over \sqrt{5} } \right) } }$

$ $　　　  $\displaystyle { = \pm { 2 \over \sqrt{5} } }$

$ $　　　  $\displaystyle { = \pm { 2 \sqrt{5} \over 5 } }$・・・（注2）

 

以上より

$ $　$\displaystyle {\cos\theta = \pm { \sqrt{5}\over 3 } }$ , $\displaystyle { \tan \theta = \pm { 2 \sqrt{5} \over 5 } }$（複号同順）・・・（注3）

（注1）「$0^\circ ＜\theta＜180^\circ$」より、単位円をかくと

$ \begin{cases}
\cos \theta ＞0（+）のとき \tan \theta ＞0（+） \\
\\
\cos \theta ＜0（−）のとき \tan \theta ＜0（−） \\
\end{cases}$

なので、$\cos \theta$ 2乗を外すときに「正（+）の平方根」と「負（−）の平方根」の両方ともOKということです。

 

（注2）ここの計算は以下のように分けて書いてもOK。

・$\displaystyle {\cos\theta = { \sqrt{5}\over 3 } }$ のとき

$ $　$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$

$ $　　　  $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$

$ $　　　  $\displaystyle { = { 2 \over 3 } \cdot { 3 \over \sqrt{5} } }$

$ $　　　  $\displaystyle { = { 2 \over \sqrt{5} } }$

$ $　　　  $\displaystyle { = { 2 \sqrt{5} \over 5 } }$

 

・$\displaystyle {\cos\theta = − { \sqrt{5}\over 3 } }$ のとき

$ $　$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$

$ $　　　  $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$

$ $　　　  $\displaystyle { = { 2 \over 3 } \cdot {  \left( − { 3 \over \sqrt{5} } \right) } }$

$ $　　　  $\displaystyle { = − { 2 \over \sqrt{5} } }$

$ $　　　  $\displaystyle { = − { 2 \sqrt{5} \over 5 } }$

以上より

$ $　$\displaystyle { (\cos\theta, \tan \theta) = \left( { \sqrt{5}\over 3 } , { 2 \sqrt{5} \over 5 } \right), \left( −{ \sqrt{5}\over 3 } , − { 2 \sqrt{5} \over 5 } \right) }$

 

（注3） 「複号同順」について

$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{5}\over 3 } } , \displaystyle { \tan \theta = { 2 \sqrt{5} \over 5 } } （+と+が対応）\\
\\
\displaystyle { \cos \theta = − { \sqrt{5}\over 3 } }, \displaystyle { \tan \theta = − { 2 \sqrt{5} \over 5 } }  （−と−が対応）\\
\end{cases}$

と同じ意味。

(3) $ \displaystyle { \tan \theta = − { 1 \over \sqrt{5} } } $ $\displaystyle { \left( 0^\circ＜\theta＜360^\circ \right) }$

今度は $ \tan \theta$ の値が与えられているので、

という流れが一番ラクそうですね。

【解答・解説】を見る

【解答】

$ $　$\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $

に $ \displaystyle { \tan \theta = − { 1 \over \sqrt{5} } } $ を代入して

$ $　$\displaystyle { 1 + \left( − { 1 \over \sqrt{5} } \right)^2 = {1 \over \cos^2 \theta} } $

$ $　∴ $\displaystyle { {1 \over \cos^2 \theta} = { 6 \over 5 } } $

両辺の逆数をとって

$ $　$\displaystyle { \cos^2 \theta = { 5 \over 6 } } $

 

ここで、「$0^\circ ＜\theta＜360^\circ$ かつ $\tan \theta ＜0$ 」すなわち

「$90^\circ ＜\theta＜180^\circ$ , $270^\circ ＜\theta＜360^\circ$」より

$ $　$\displaystyle { \cos\theta = \pm { \sqrt{ 5 \over 6 } } }$

$ $　　　  $= \displaystyle { \pm  { \sqrt{30} \over 6 } } $・・・（注1）

 

また、

$ $　$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$

の両辺に $ \cos \theta $ をかけて

$ $　$\displaystyle { \tan \theta \cdot \cos \theta = {\sin \theta \over \require{cancel} \bcancel{ \cos \theta } } \cdot \bcancel{ \cos \theta } }$

左辺と右辺を入れ替えて

$ $　$\displaystyle { \sin \theta = \tan \theta \cdot \cos \theta }$

$ $　　　$\displaystyle { = − { 1 \over \sqrt{5} } \cdot \left( \pm { \sqrt{30} \over 6 } \right) }$

$ $　　　$\displaystyle { = \mp { \sqrt{6} \over 6 } }$ ・・・（注2）

 

以上より

$ $　$\displaystyle {\cos\theta = \pm { \sqrt{30} \over 6 } }$ , $\displaystyle { \sin \theta = \mp { \sqrt{6} \over 6 } }$（複号同順）・・・（注3）

（注1）「$90^\circ ＜\theta＜180^\circ$ , $270^\circ ＜\theta＜360^\circ$」より、単位円をかくと

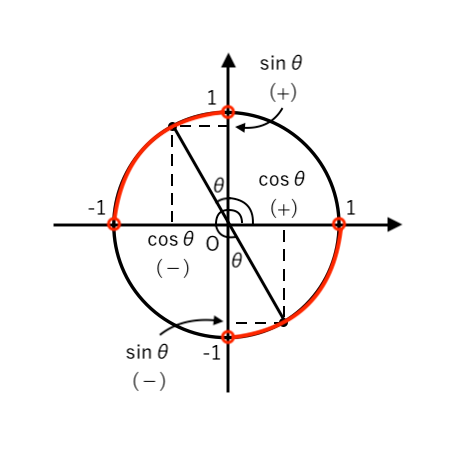
$ \begin{cases}
\cos \theta ＞0（+）のとき \sin \theta ＜0（−） \\
\\
\cos \theta ＜0（−）のとき \sin \theta ＞0（+） \\
\end{cases}$

なので、$\cos \theta$ 2乗を外すときに「正（+）の平方根」と「負（−）の平方根」の両方ともOKということですね。

 

（注2）ここの計算は以下のように分けて書いてもOK。

・$\displaystyle {\cos\theta = { \sqrt{30} \over 6 } }$ のとき

$ $　$\displaystyle { \sin \theta = \tan \theta \cdot \cos \theta }$

$ $　　　$\displaystyle { = − { 1 \over \sqrt{5} } \cdot { \sqrt{30} \over 6 } }$

$ $　　　$\displaystyle { = − { \sqrt{6} \over 6 } }$

 

・$\displaystyle {\cos\theta = − { \sqrt{30} \over 6 } }$ のとき

$ $　$\displaystyle { \sin \theta = \tan \theta \cdot \cos \theta }$

$ $　　　$\displaystyle { = − { 1 \over \sqrt{5} } \cdot \left( − { \sqrt{30} \over 6 } \right) }$

$ $　　　$\displaystyle { = { \sqrt{6} \over 6 } }$

以上より

$ $　$\displaystyle { (\cos\theta, \sin \theta) = \left( { \sqrt{30} \over 6 } , − { \sqrt{6} \over 6 } \right), \left( −{ \sqrt{30} \over 6 } , { \sqrt{6} \over 6 } \right) }$

 

（注3） 「複号同順」について

$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{30} \over 6 } } , \displaystyle { \sin \theta = − { \sqrt{6} \over 6 } } （+と−が対応）\\
\\
\displaystyle { \cos \theta = − { \sqrt{30} \over 6 } }, \displaystyle { \sin \theta = { \sqrt{6} \over 6 } }  （−と+が対応）\\
\end{cases}$

と同じ意味。

【三角比の相互関係】テストによくでる応用問題 Lv.1 (式を簡単に)

「次の式を簡単にせよ。」というタイプの問題です。

「三角比の相互関係」の公式を使ってうまく変形していきます。

(1) $\displaystyle { { \cos\theta \over 1−\sin\theta } + { 1−\sin\theta \over \cos\theta } }$

分数の形なのでとりあえず通分すると、三角比の相互関係が使えそうな形になってくれます。

【解答・解説】を見る

【解答】

$\displaystyle { { \cos\theta \over 1−\sin\theta } + { 1−\sin\theta \over \cos\theta } }$

$\displaystyle { = { \cos^2 \theta + ( 1−\sin\theta )^2 \over ( 1−\sin\theta )\cos\theta } }$

$\displaystyle { = { \color{red}{ \cos^2 \theta } + 1−2 \sin\theta + \color{red}{ \sin^2 \theta } \over ( 1−\sin\theta )\cos\theta } }$

$\displaystyle { = { \color{red}{ 1 } + 1−2 \sin\theta \over ( 1−\sin\theta )\cos\theta } }$　$ \left( \color{red} { \sin^2 \theta + \cos^2 \theta } = 1 を代入 \right) $

$\displaystyle { = { 2−2 \sin\theta \over ( 1−\sin\theta )\cos\theta } }$

$\displaystyle { = { 2 \require{cancel} \bcancel{ ( 1− \sin\theta ) } \over \bcancel{ ( 1−\sin\theta ) } \cos\theta } }$

$\displaystyle { = { 2 \over \cos\theta } }$

(2) $ \sin (90^\circ − \theta) \cos (180^\circ − \theta)− \cos^2 \theta \tan^2 ( 180^\circ − \theta )$

まずは

• 「$90^\circ − \theta$」→ 余角公式
• 「$180^\circ − \theta$」→ 補角公式

を使って変形します。

【解答・解説】を見る

【解答】

$ \begin{cases}
\color{red} {\sin (90^\circ − \theta)} = \cos \theta \\
\\
\color{green} {\cos (180^\circ − \theta)} = − \cos \theta \\
\\
\color{blue} {\tan ( 180^\circ − \theta )} = − \tan \theta \\
\end{cases}$

より

$ \color{red} {\sin (90^\circ − \theta)} \color{green} {\cos (180^\circ − \theta)} − \cos^2 \theta \enspace \color{blue} {\tan}^2 \color{blue} {( 180^\circ − \theta )} $

$ = \color{red} {\cos \theta} \cdot ( \color{green} { −\cos \theta } ) − \cos^2 \theta \cdot ( \color{blue} {−\tan \theta} )^2 $

$ = − \cos^2 \theta − \cos^2 \theta \tan ^2 \theta $

$ = − \cos^2 \theta − \cos^2 \theta \left( \displaystyle {\sin \theta \over \cos \theta } \right)^2 $　$ \left( \displaystyle { \tan \theta = {\sin \theta \over \cos \theta} } を代入 \right) $

$ \displaystyle { = − \cos^2 \theta − \require{cancel} \bcancel{ \cos^2 \theta } \cdot { \sin^2 \theta \over \bcancel{ \cos^2 \theta } } } $

$ = − \cos^2 \theta − \sin^2 \theta $

$ = − ( \cos^2 \theta + \sin^2 \theta ) $

$ = −1 $　　（$\sin^2 \theta + \cos^2 \theta = 1$ を代入）

（注）「余角公式」「補角公式」は暗記するのではなく、単位円をかいて考えましょう。

✔︎ $\sin (90^\circ − \theta) = \cos \theta$

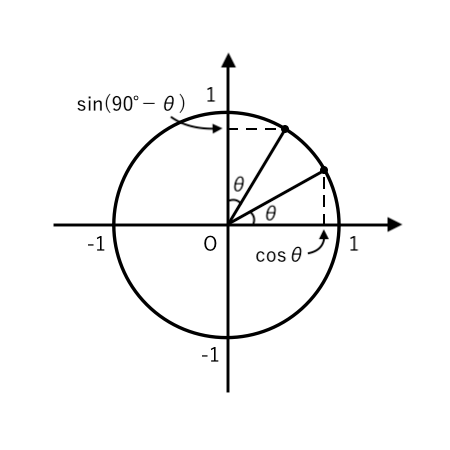
✔︎ $\cos (180^\circ − \theta) = − \cos \theta$

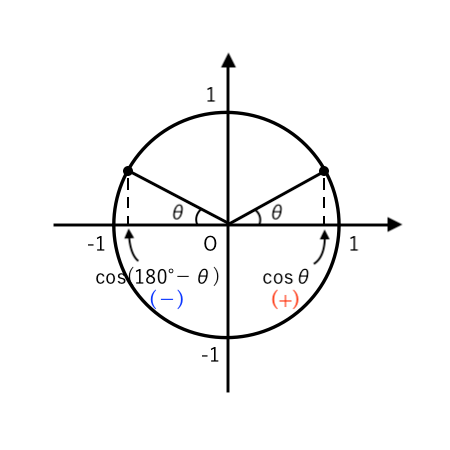
✔︎ $\tan ( 180^\circ − \theta ) = − \tan \theta$

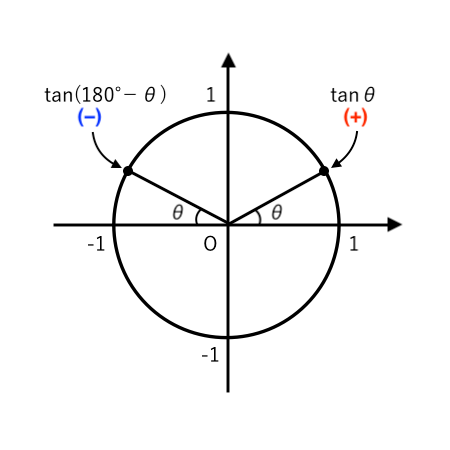
慣れてきたら頭の中でイメージするだけでもOK。

【三角比の相互関係】テストによくでる応用問題 Lv.2 (値を代入)

Lv.1の問題で学んだ考え方を活かして解いてみましょう！

(1) $ \displaystyle { \sin \theta − \cos \theta \over \sin \theta + \cos \theta } $

「三角比の相互関係」の公式 $\displaystyle { {\sin \theta \over \cos \theta} = \tan \theta }$ をイメージすると方針が浮かんできます。

【解答】を見る

【解答】

$ \displaystyle { \sin \theta − \cos \theta \over \sin \theta + \cos \theta } $

$ = \displaystyle { \displaystyle { {\sin \theta \over \cos \theta} − { \require{cancel} \bcancel{ \cos \theta } \over \require{cancel} \bcancel{ \cos \theta } } } \over \displaystyle { {\sin \theta \over \cos \theta} + { \require{cancel} \cancel{ \cos \theta } \over \require{cancel} \cancel{ \cos \theta} } } } $

$ $　（分母・分子ともに ${\cos \theta}$ で割る）

$ = \displaystyle { \displaystyle { {\sin \theta \over \cos \theta} −1 } \over \displaystyle { {\sin \theta \over \cos \theta} + 1 } } $

$ = \displaystyle { \displaystyle { \tan \theta −1 } \over \displaystyle { \tan \theta + 1 } } $　$\displaystyle { \left( {\sin \theta \over \cos \theta} = \tan \theta を代入 \right) }$

$ = \displaystyle { \displaystyle { −{1 \over 2} −1 } \over \displaystyle { −{1 \over 2} + 1 } } $　$\displaystyle { \left( \tan \theta = −{1 \over 2} を代入 \right) }$

$ = \displaystyle { \displaystyle { −{3 \over 2} } \over \displaystyle { 1 \over 2 } } $

$ = \displaystyle { \displaystyle { −{3 \over 2} ×2 } \over \displaystyle { {1 \over 2}×2 } } $ ・・・（注）

$ = \displaystyle { −3 } $

（注）分数の中に分数が入っているときは、「分母 $\left( \displaystyle { { 1 \over 2 } } \right)$ と分子 $\left( \displaystyle {−{ 3  \over 2 } } \right)$ に同じ数 $\left( 2 \right)$ をかける」と考えるといいです。

あるいは、「割り算（分子 ÷ 分母）」とみなして

$ $　$ \displaystyle { \displaystyle { −{3 \over 2} } \over \displaystyle { {1 \over 2} } } $

$ $　$ = \displaystyle { \displaystyle { −{3 \over 2} } ÷ \displaystyle { {1 \over 2} } } $

$ $　$ = \displaystyle { \displaystyle { −{3 \over 2} ×2 }  } $

と計算してもOK。

(2) $ \displaystyle { {1 \over 1 + \cos \theta} + {1 \over 1 − \cos \theta}  } $

分数を 通分 すると道が開けます。

【解答】を見る

【解答】

$ \displaystyle { {1 \over 1 + \cos \theta} + {1 \over 1 − \cos \theta}  } $

$ = \displaystyle { ( 1− \cos \theta ) + ( 1 + \cos \theta ) \over ( 1 + \cos \theta )( 1 − \cos \theta ) } $

$ = \displaystyle { 1− \require{cancel} \bcancel{ \cos \theta } + 1 + \require{cancel} \bcancel{ \cos \theta } \over ( 1 + \cos \theta )( 1 − \cos \theta ) } $

$ = \displaystyle { 2 \over 1 − \cos^2 \theta } $

 

ここで

$ $　$\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $

の両辺の逆数をとって

$ $　$\displaystyle { {1 \over 1 + \tan^2 \theta } = \cos^2 \theta } $

左辺と右辺を入れ替えて

$ $　$\displaystyle { \cos^2 \theta = {1 \over 1 + \tan^2 \theta } } $

$ $　　　　$\displaystyle { = {1 \over \displaystyle { 1 + \left( −{1 \over 2} \right)^2 } } } $　$\displaystyle { \left( \tan \theta = −{1 \over 2} を代入 \right) }$

$ $　　　　$\displaystyle { = { \enspace 1 \enspace \over \displaystyle { 5 \over 4 } } } $

$ $　　　　$\displaystyle { = { 1 ×4 \over \displaystyle { {5 \over 4}×4 } } } $

$ $　　　　$\displaystyle { = \color{red}{ 4 \over 5 } } $

 

よって

（与式）$ = \displaystyle { 2 \over 1 − \color{red}{ \cos^2 \theta } } $

$ $　　$ = \displaystyle { 2 \over \displaystyle { 1 − \color{red}{ 4 \over 5 } } } $

$ $　　$ = \displaystyle { \enspace 2 \enspace \over \displaystyle { { 1\over 5 } } } $

$ $　　$ = \displaystyle { 2×5 \over \displaystyle { { 1\over 5 } ×5 } } $

$ $　　$ = \displaystyle { 10 } $

【三角比の相互関係】テストによくでる応用問題 Lv.3 (対称式)

三角比に「対称式（交代式）」が絡んでくる応用問題は、学校のテスト・入試にもよく出ます。

「対称式（交代式）」のおさらいをしたい人はこちら。

関連記事

【高校数学】対称式（交代式）の解き方をわかりやすく解説【基本定理はこれだけ覚えよう】

対称式・交代式の解き方がよくわからない そもそも対称式って何？ 対称式のわかりやすい解説が聞きたい！ 今回はこういった疑問・要望にお答えします。 対称式（交代式）の問題は、解法が完全にパターン化されています（やり方が決ま[…]

それではやっていきましょう！

(1) $\sin \theta \cos \theta$

「$\sin \theta$ と $\cos \theta$ の積」の形は「$\sin \theta$ と $\cos \theta$ の和」を2乗すると作れます。

【解答・解説】を見る

【解答】

$ $　$ \sin \theta + \cos \theta = \displaystyle {2 \over 3} $・・・①

①の両辺を2乗して

$ $　$ \left( \sin \theta + \cos \theta \right)^2 = \left( \displaystyle {2 \over 3} \right)^2 $

$ $　∴ $ \color{red} {\sin^2 \theta} + 2 \sin \theta \cos \theta + \color{red} {\cos^2 \theta} = \displaystyle {4 \over 9 } $

ここに $ \color{red} {\sin^2 \theta + \cos^2 \theta} = 1$ を代入して

$ $　$ \color{red} {1} + 2 \sin \theta \cos \theta = \displaystyle { 4 \over 9 } $

$ $　∴ $ 2 \sin \theta \cos \theta = − \displaystyle { 5 \over 9 } $

$ $　∴ $ \sin \theta \cos \theta = − \displaystyle { 5 \over 18 } $ ・・・②

(2) $\sin^3 \theta + \cos^3 \theta$

3乗の形を作るために「展開の公式」を利用します。

別解として、「因数分解の公式」を使ってもできます。

【別解】を見る

【別解】

$ \sin^3 \theta + \cos^3 \theta $

$ = ( \color{red} { \sin \theta + \cos \theta } ) ( \sin^2 \theta − \color{green} { \sin \theta \cos \theta  } + \cos^2 \theta ) $

ここに

$ \begin{cases}
\sin^2 \theta + \cos^2 \theta = 1 \\
\\
① \color{red} { \sin \theta + \cos \theta } = \displaystyle { 2 \over 3 } \\
\\
② \color{green} { \sin \theta \cos \theta } = − \displaystyle { 5 \over 18 } \\
\end{cases}$

を代入して

（与式）$\displaystyle { = \color{red} { 2 \over 3 } \left\{ 1 − \left( \color{green} { −  { 5 \over 18 } } \right) \right\} } $

$ $　　　　$ \displaystyle { = { 2 \over 3 } \cdot { 23 \over 18 } } $

$ $　　　　$ \displaystyle { = { 23 \over 27 } } $

(3) $\sin \theta − \cos \theta$

$\sin \theta − \cos \theta$ の値をいきなり求めることはできませんが、

とりあえず 2 乗した形  $ ( \sin \theta − \cos \theta )^2 $ なら分かりそうですよね？

【解答・解説】を見る

【解答】

$ ( \sin \theta − \cos \theta )^2 $

$ = \color{red} { \sin^2 \theta } − 2 \color{green} { \sin \theta \cos \theta } + \color{red} { \cos^2 \theta } $

$ = \color{red} { 1 } − 2 \cdot \left( \color{green} { − \displaystyle { 5 \over 18 } } \right)  $　$ \left( \color{red} { \sin^2 \theta + \cos^2 \theta } = 1 、 ② \color{green} { \sin \theta \cos \theta } = − \displaystyle { 5 \over 18 } を代入 \right) $

$ \displaystyle { = 1 + { 5 \over 9 } } $

$ \displaystyle { = { 14 \over 9 } } $

 

ここで、$0^\circ ≦\theta≦180^\circ$ より $\sin \theta ≧ 0$ ・・・（注1）

また、$\sin \theta \cos \theta ＜0$ より $\sin \theta$、$\cos \theta$ は異符号。

これらを合わせて考えると $\cos \theta ＜0$ ・・・（注2）

∴ $− \cos \theta ＞0$

 

「$\sin \theta ≧ 0$ かつ $− \cos \theta ＞0$」より

$\sin \theta − \cos \theta ＞0 $・・・（注3）

 

ゆえに

$ \displaystyle { \sin \theta − \cos \theta = \sqrt{ 14 \over 9 } }$

$ $　　　　　$ \displaystyle { = { \sqrt{ 14 } \over 3 } } $・・・③

（注1）「$0^\circ ≦\theta≦180^\circ$」より、単位円をかくと

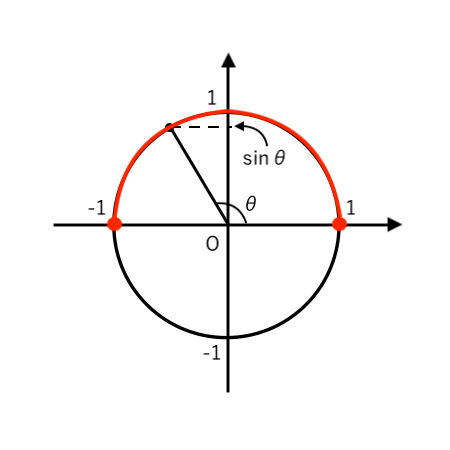
なので、$\sin \theta ≧ 0$（$0$以上）とわかります。

 

（注2）$\sin \theta \cos \theta ＜0$（かけてマイナス）ということは

$\sin \theta$、$\cos \theta$ のうち一方は「+」、もう一方は「−」（異符号）になります。

上記の(注1)より $\sin \theta ≧ 0$（$\color{red}{0}$以上）なので、もう一方の $\cos \theta$ は「−」と分かります。

 

（注3）$\sin \theta − \cos \theta$ は、

「$\sin \theta ≧ 0$（$\color{red}{0}$以上）」と「$− \cos \theta ＞0$（+）」を足した数なので

$\sin \theta − \cos \theta＞0$（+）になります。

別解として、$ \color{red} {\cos \theta} $ を消去して「$ \sin \theta $ の2次方程式」を解くやり方もあります。

【別解】を見る

【別解】

$ \sin \theta + \cos \theta = \displaystyle {2 \over 3} $ より

$ $　$ \color{red} {\cos \theta} = \displaystyle {2 \over 3} − \sin \theta $

これを

$ $　$ \sin^2 \theta + \color{red} {\cos}^2 \color{red} {\theta} = 1$

に代入して

$ $　$ \displaystyle { \sin^2 \theta + \left( \color{red} { {2 \over 3} − \sin \theta } \right)^2 } = 1$

$ $　∴ $ \displaystyle { \sin^2 \theta + \left( {4 \over 9} −{4 \over 3}\sin \theta + \sin^2 \theta \right) } = 1$

$ $　∴ $ \displaystyle { 2 \sin^2 \theta −{4 \over 3}\sin \theta + {4 \over 9} } = 1$

両辺に $9$ をかけて

$ $　$ \displaystyle { 18 \sin^2 \theta −12 \sin \theta + 4 } = 9 $

$ $　∴ $ \displaystyle { 18 \sin^2 \theta −12 \sin \theta −5 = 0 }$

これを $\sin \theta$ についての2次方程式と見て、解を求めると

$ $　$ \displaystyle { \sin \theta = { 6 \pm \sqrt{ 36 −18 \cdot (−5) } \over 18 } }$ ・・・（注1）

$ $　　　$ \displaystyle { = { 6 \pm \sqrt{ 126 } \over 18 } }$

$ $　　　$ \displaystyle { = { 6 \pm 3 \sqrt{ 14 } \over 18 } }$

$ $　　　$ \displaystyle { = { 2 \pm \sqrt{ 14 } \over 6 } }$

 

ここで、$0^\circ ≦\theta≦180^\circ$ より　$ 0 ≦\sin \theta≦1 $

$ $　∴ $ \displaystyle { \color{green} {\sin \theta} = { 2 + \sqrt{ 14 } \over 6 } }$ ・・・（注2）

 

よって

$ $　$ \cos \theta = \displaystyle {2 \over 3} − \color{green} {\sin \theta} $

$ $　　$ = \displaystyle {2 \over 3} − \color{green} { 2 + \sqrt{ 14 } \over 6 } $

$ $　　$ = \displaystyle { 2 − \sqrt{ 14 } \over 6 } $

 

ゆえに

$ $　$\sin \theta −\cos \theta$

$ $　$ \displaystyle { = { 2 + \sqrt{ 14 } \over 6 } − { 2 − \sqrt{ 14 } \over 6 } } $

$ $　$ \displaystyle { = { \sqrt{ 14 } \over 3 } } $

（注1）$ \displaystyle { 18x^2 −12x −5 = 0 }$ の解き方について

ふつうの解の公式を使ってしまうと

$ $　$ \displaystyle { x = { 12 \pm \sqrt{ 12^2 −4 \cdot 18 \cdot (−5) } \over 2 \cdot 18 } }$

となって計算が大変ですね。

そこで

$x$ の2次方程式  $ax^2 + bx + c = 0$

において $b$ が偶数のとき、$b = 2b’$ とすると

$ \displaystyle { x = { −b’ \pm \sqrt{ b’^2 − ac } \over a } }$

これを利用すると

$ $　$ \displaystyle { x = { 6 \pm \sqrt{ 6^2 − 18 \cdot (−5) } \over 18 } }$

と、ちょっとだけ楽ができます。

 

（注2）ここで

「$\displaystyle { \sin \theta = { 2 + \sqrt{ 14 } \over 6 } } $ は、$ 0 ≦\sin \theta≦1 $ の範囲にホントに入ってるの？$\sqrt{ 14 }$ の値なんて覚えてないよ〜」

と思ったキミへ・・・

もし $\sqrt{ 14 }$ の値を知らなくても

$ $　$3^2 ＜ 14＜ 4^2$ より　$3 ＜\sqrt{ 14 }＜ 4$

というのは分かりますよね？

ここから $\displaystyle { 2 + \sqrt{ 14 } \over 6 }$ の形に少しずつ近づけていきます。

 

$ $　$3 ＜\sqrt{ 14 }＜ 4$

辺々に $2$ を足して

$ $　$5 ＜2 + \sqrt{ 14 }＜ 6$

辺々を $6$ で割って

$ $　$\displaystyle { {5 \over 6}＜ { 2 + \sqrt{ 14 } \over 6 }＜{6 \over 6} }$

$ $　∴ $\displaystyle { {5 \over 6}＜\sin \theta＜1 }$

となり、$ 0 ≦\sin \theta≦1 $ を満たしていることが分かりました。

この変形のしかたは、これ以外にも 2次関数など色んな場面で必要となります。

バッチリ覚えておきましょう！

(4) $\sin \theta $

「$\sin \theta$ と $\cos \theta$ の和・差」が分かっているので、そこから $\sin \theta$ の値を求められます。

【解答・解説】を見る

【解答】

$ \begin{cases}
① \sin \theta + \cos \theta = \displaystyle { 2 \over 3 } \\
\\
③ \sin \theta − \cos \theta  = \displaystyle { \sqrt{ 14 } \over 3 } \\
\end{cases}$

の辺々を足して

$ $　$ \displaystyle { ( \sin \theta + \require{cancel} \bcancel{ \cos \theta } ) + ( \sin \theta − \bcancel{ \cos \theta } ) =  { 2 \over 3 } + { \sqrt{ 14 } \over 3 } } $

$ $　∴ $ \displaystyle { 2 \sin \theta =  { 2 + \sqrt{ 14 } \over 3 } } $

$ $　∴ $ \displaystyle { \sin \theta = { 1 \over 2 } \cdot { 2 + \sqrt{ 14 } \over 3 } } $

$ $　　　　 $ \displaystyle { =  { 2 + \sqrt{ 14 } \over 6 } } $

(5) $\displaystyle { \tan \theta − { 1 \over \tan \theta } }$

$\tan \theta $ を消去 → 分数を通分 → 因数分解 すると、対称式が代入できそうな形になります。

【解答・解説】を見る

【解答】

$\displaystyle { \tan \theta − { 1 \over \tan \theta } }$

$\displaystyle { = { \sin \theta \over \cos \theta } − { \cos \theta \over \sin \theta } }$　$\displaystyle { \left( \tan \theta = {\sin \theta \over \cos \theta} を代入 \right) }$

$\displaystyle { = { \sin^2 \theta − \cos^2 \theta \over \sin \theta \cos \theta } }$　・・・（注1）

$\displaystyle { = { ( \color{red} { \sin \theta + \cos \theta } ) ( \color{blue} { \sin \theta − \cos \theta } ) \over \color{green} { \sin \theta \cos \theta } } }$

 

ここに

$ \begin{cases}
① \color{red} { \sin \theta + \cos \theta } = \displaystyle { 2 \over 3 } \\
\\
② \color{green} { \sin \theta \cos \theta } = − \displaystyle { 5 \over 18 } \\
\\
③ \color{blue} { \sin \theta − \cos \theta } = \displaystyle { \sqrt{ 14 } \over 3 } \\
\end{cases}$

を代入して

（与式）$\displaystyle { = { \displaystyle { \color{red} { 2 \over 3 } \cdot \color{blue} { \sqrt{14} \over 3 } } \over \displaystyle { \color{green} {−{ 5 \over 18 } } } } } $

$ $　　　　$\displaystyle { = { \enspace  \displaystyle { 2 \sqrt{14} \over 9 } \enspace \over \displaystyle {−{ 5 \over 18 } } } } $

$ $　　　　$\displaystyle { = { \displaystyle { { 2 \sqrt{14} \over 9 }× 18 } \over \displaystyle {−{ 5 \over 18 }× 18 } } } $ ・・・（注2）

$ $　　　　$\displaystyle { = − { 4 \sqrt{14} \over 5 } } $

（注1）ここの通分の流れは、例えば

$ $　$\displaystyle { { 4 \over 5 } − { 5 \over 4 } } $

$ $　$\displaystyle { = { 4^2 \over 5 \cdot 4 } − { 5^2 \over 4 \cdot 5 } } $

$ $　$\displaystyle { = { 4^2 − 5^2 \over 5 \cdot 4 } } $

と同様に考えると

$ $　$\displaystyle { { \sin \theta \over \cos \theta } − { \cos \theta \over \sin \theta } }$

$ $　$\displaystyle { = { \sin^2 \theta \over \cos \theta \sin \theta } − { \cos^2 \theta \over \sin \theta \cos \theta } }$

$ $　$\displaystyle { = { \sin^2 \theta − \cos^2 \theta \over \sin \theta \cos \theta } }$

 

（注2）分数の中に分数が入っているときは、「分母 $\left( \displaystyle {−{ 5 \over 18 } } \right)$ と分子 $\left( \displaystyle { 2 \sqrt{14} \over 9 } \right)$ に同じ数 $\left( 18 \right)$ をかける」と考えるといいです。

あるいは、「割り算（分子 ÷ 分母）」とみなして

$ $　$\displaystyle { { \enspace \displaystyle { 2 \sqrt{14} \over 9 } \enspace \over \displaystyle {−{ 5 \over 18 } } } } $

$ $　$\displaystyle { = { 2 \sqrt{14} \over 9 } ÷ \left(−{ 5 \over 18 } \right) } $

$ $　$\displaystyle { = { 2 \sqrt{14} \over 9 } × \left(−{ 18 \over 5 } \right) } $

と計算してもOK。

Study more！三角比の対称式（交代式）

「三角比の対称式」の問題をもっと解きたい！という人はこちらもどうぞ。

関連記事

【高校数学】三角比の対称式（交代式）の問題【テスト・入試によく出るパターンを網羅！】

三角比の対称式（交代式）で、テストや大学入試によく出るパターンの問題を網羅したい！ 三角比の対称式を、基礎からはじめて 入試の基本レベルまで徐々に学んでいきたい！ こういった要望をお持ちの人に向けて、この記事を書きました。 &[…]

【三角比の相互関係】テストによくでる応用問題 Lv.4 (三角方程式)

大きさが未知の角 $\theta$ の三角比を含む方程式を「三角方程式」と言います。

三角方程式も「三角比の相互関係」を使って解くことが多いです。

(1) $ 2 \cos^2 \theta + 3 \sin \theta − 3 = 0 $

$ \cos \theta$ と $ \sin \theta$ が混ざっていて考えにくいので、まずは片方だけにしたいですね。

「三角比の相互関係」を使うと $ \sin \theta$ だけの式に変形できそうです。

【解答・解説】を見る

【解答】

$ \sin^2 \theta + \cos^2 \theta = 1 $ より

$ $　$ \color{red} { \cos^2 \theta } = 1 −\sin^2 \theta $

$ 2 \color{red} { \cos^2 \theta } + 3 \sin \theta − 3 = 0 $ に代入して

$ $　$ 2 ( \color{red} { 1 −\sin^2 \theta } ) + 3 \sin \theta − 3 = 0 $

$ $　∴ $ 2 − 2 \sin^2 \theta + 3 \sin \theta − 3 = 0 $

$ $　∴ $ − 2 \sin^2 \theta + 3 \sin \theta − 1 = 0 $

両辺の符号を逆にして（$−1$をかけて）

$ $　$ 2 \sin^2 \theta − 3 \sin \theta + 1 = 0 $

$ $　∴ $ ( 2 \sin \theta −1 ) ( \sin \theta −1 ) = 0 $ ・・・（注1）

$ $　∴ $ \displaystyle { \sin \theta = { 1 \over 2 }, 1 } $

$0^\circ ≦\theta≦180^\circ$ より　　　　　・・・（注2）

$ \begin{cases}
\displaystyle { \sin \theta = { 1 \over 2 } } \enspace のとき \enspace \theta = 30^\circ , 150^\circ \\
\\
\displaystyle { \sin \theta = 1 } \enspace のとき \enspace \theta = 90^\circ \\
\end{cases}$

よって

$ $　$ \theta = 30^\circ , 90^\circ , 150^\circ $

（注1）ここの因数分解は、2次方程式 $ 2 x^2 − 3 x + 1 = 0 $ で考えると

$ $　$ ( 2 x −1 ) ( x−1 ) = 0 $

$ $　∴ $ \displaystyle { x = { 1 \over 2 }, 1 } $

これの $x$ を $\sin \theta$ で置き換えればもとの形になります。

 

（注2）$0^\circ ≦\theta≦180^\circ$ の範囲で

$ $　$ \displaystyle { \sin \theta = { 1 \over 2 }, 1 } $

となるような $\theta$ を考えると

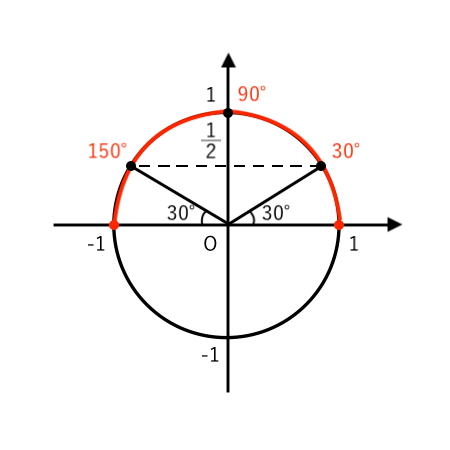
この3つになりますね。

(2) $ \displaystyle { \left| \cos \theta − { 1 \over 2 } \right| = { 1 \over 2 } } $

絶対値の中に三角比が入っている問題です。

「絶対値の外し方」をおさらいしたい人はこちら。

関連記事

【高校数学】絶対値のついた等式・不等式の解き方をわかりやすく解説【場合分けもバッチリ】

この記事では、絶対値記号のついた等式・不等式の解き方 を解説します。 絶対値の問題は等式・不等式で解き方が変わったり、場合分け が必要になったりするので意外とつまづく生徒が多いです。 |x| = 5　を解くと、どうして　x = ± […]

例えば

$ $　$|x| = 2$

の絶対値を外すと

$ $　$x = \pm 2$

の2つ出てきましたね。

【解答・解説】を見る

【解答】

$ $　$ \displaystyle { \left| \cos \theta − { 1 \over 2 } \right| = { 1 \over 2 } } $

$ $　∴ $ \displaystyle { \cos \theta − { 1 \over 2 } = \pm { 1 \over 2 } } $

$ $　∴ $ \displaystyle { \cos \theta = { 1 \over 2 } \pm { 1 \over 2 } } $

$ $　∴ $ \displaystyle { \cos \theta = 1 , 0 } $

$0^\circ ≦\theta≦180^\circ$ より　・・・（注）

$ \begin{cases}
\cos \theta = 1 \enspace のとき \enspace \theta = 0^\circ \\
\\
\cos \theta = 0 \enspace のとき \enspace \theta = 90^\circ \\
\end{cases}$

よって

$ $　$ \theta = 0^\circ , 90^\circ $

（注）$0^\circ ≦\theta≦180^\circ$ の範囲で

$ $　$ \displaystyle { \cos \theta = 1 , 0 } $

となるような $\theta$ を考えると

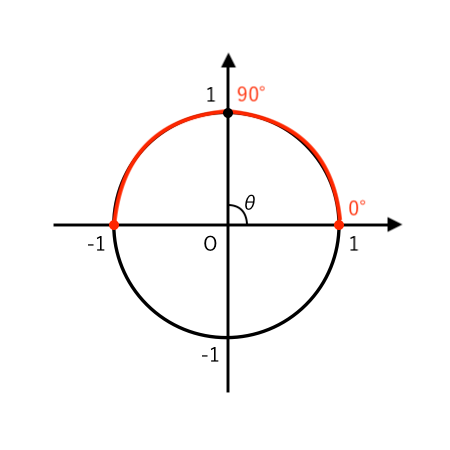
この2つになります。

別解として「絶対値の形がイヤなので、はじめに 2乗して絶対値を消す やり方」もOK。

【別解】を見る

【別解】

$ $　$ \displaystyle { \left| \cos \theta − { 1 \over 2 } \right| = { 1 \over 2 } } $

の両辺を2乗して

$ $　$ \displaystyle { \left( \cos \theta − { 1 \over 2 } \right)^2 = \left( { 1 \over 2 } \right)^2 } $

$ $　∴ $ \displaystyle { \cos^2 \theta −\cos \theta + { 1 \over 4 } = { 1 \over 4 } } $

$ $　∴ $ \displaystyle { \cos^2 \theta −\cos \theta = 0 } $

$ $　∴ $ \displaystyle { \cos \theta \enspace ( \cos \theta−1 ) = 0 } $

$ $　∴ $ \displaystyle { \cos \theta = 0 , 1 } $

$0^\circ ≦\theta≦180^\circ$ より

$ $　$ \theta = 0^\circ , 90^\circ $

どちらのやり方でも出来るようにしておくと、

視野が広がって応用が効くようになる のでオススメです。

ちなみに、もし今回の問題が

$ $　$ \displaystyle { \left| \cos \theta − { 1 \over 2 } \right| = { 1 \over 2 } \cos \theta } $

というような形の場合、

$ $　$ \displaystyle { \cos \theta − { 1 \over 2 } = \pm { 1 \over 2 } \cos \theta } $

とやってしまうと「×」です（もしくは大きく減点されます）。

「え〜なんで〜！？」と思った人は、以下の記事内【パターン3】を読んでおきましょう。

関連記事

【高校数学】絶対値のついた等式・不等式の解き方をわかりやすく解説【場合分けもバッチリ】

この記事では、絶対値記号のついた等式・不等式の解き方 を解説します。 絶対値の問題は等式・不等式で解き方が変わったり、場合分け が必要になったりするので意外とつまづく生徒が多いです。 |x| = 5　を解くと、どうして　x = ± […]

【三角比の相互関係】テストによくでる応用問題 Lv.5 (２次関数)

いよいよ最後の問題です。

三角比と「2次関数」の融合問題は、学校のテスト・大学入試ともに かなり出やすい です。

三角比 ×２次関数の最大値・最小値

解答の流れ はこんな感じ。

この流れをイメージしながら解答を書いてみましょう。

【解答・解説】を見る

【解答】

$\sin^2 \theta + \cos^2 \theta = 1$ より

$ $　$ \color{red} { \sin^2 \theta } = 1 − \cos^2 \theta $

∴ $ y = \color{red} { \sin^2 \theta } −\cos \theta $

$ $　　$ = \color{red} { ( 1 − \cos^2 \theta ) } −\cos \theta $

$ $　　$ = − \cos^2 \theta −\cos \theta + 1 $

 

ここで、$\cos \theta = t $ とおくと

$ 0^\circ≦\theta≦180^\circ $ より　$ −1≦t≦1 $ ・・・（注1）

 

よって

$ $　$ y = − t^2 −t + 1 $

$ $　　$ = − ( t^2 + t ) + 1$

$ $　　$ \displaystyle { = − \left( t + {1 \over 2} \right)^2 −\left( {1 \over 2} \right)^2 \cdot (−1) + 1 }$

$ $　　$ \displaystyle { = − \left( t + {1 \over 2} \right)^2 + {5 \over 4} }$

これは

$ \begin{cases}
頂点 \displaystyle { \left( −{1 \over 2} , {5 \over 4} \right) } \\
\\
軸： \displaystyle { t = −{1 \over 2} }  \\
\\
上に凸
\end{cases}$

の放物線。

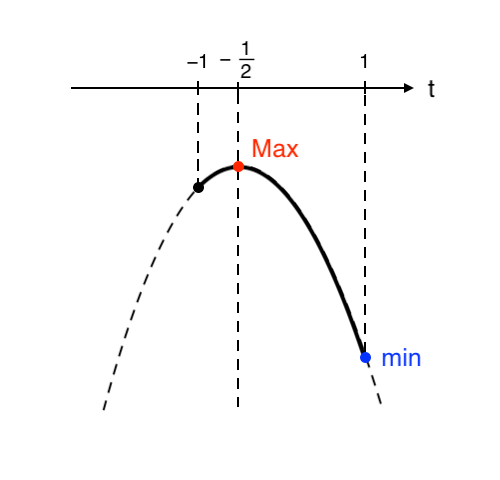
$ −1≦t≦1 $ より、$y$ は

$ \begin{cases}
t = −\displaystyle{1 \over 2} \enspace で最大値 \enspace \displaystyle{5 \over 4} \\
\\
t = 1 \enspace で最小値 \enspace−1 \\
\end{cases}$

をとる。　　・・・（注2）

 

・$ t = −\displaystyle{1 \over 2} $ のとき $\cos \theta = −\displaystyle{1 \over 2} $

$ $　$ 0^\circ≦\theta≦180^\circ $ より　$ \theta = 120^\circ $ ・・・（注3）

・$ t = 1 $ のとき $\cos \theta = 1 $

$ $　$ 0^\circ≦\theta≦180^\circ $ より　$ \theta = 0^\circ $ ・・・（注4）

 

以上より

$ \begin{cases}
\theta = 120^\circ \enspace で最大値 \enspace \displaystyle{5 \over 4} \\
\\
\theta = 0^\circ \enspace で最小値 \enspace−1 \\
\end{cases}$

（注1）$ 0^\circ≦\theta≦180^\circ $ より、$\cos \theta$ のとる範囲を 単位円で確認すると

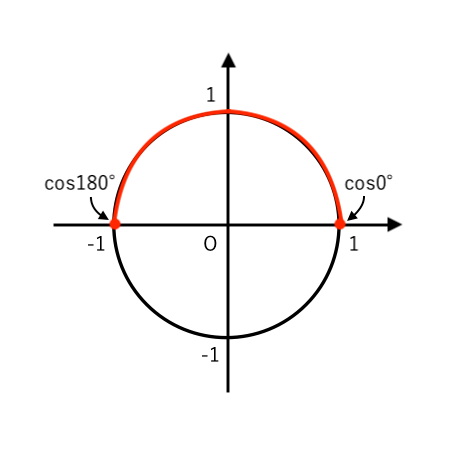
なので、$ −1≦\cos \theta≦1 $ と分かります。

 

（注2）

【2次関数のグラフ：最大値・最小値の求め方（上に凸の場合）】

① 上に凸 の放物線を（薄めに）かく

② その上に横軸（$t$ 軸）をかく

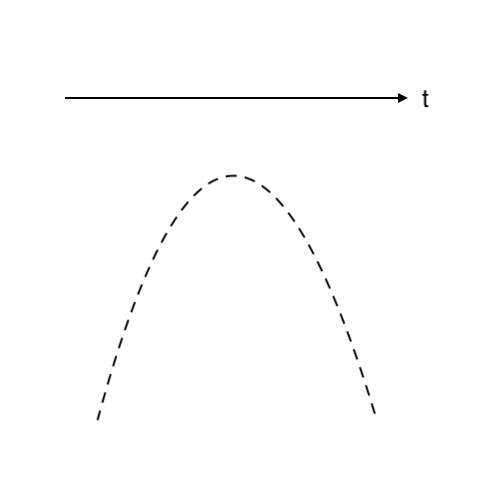
③ 「$t$の範囲の端っこ」「放物線の軸」の値 をとる

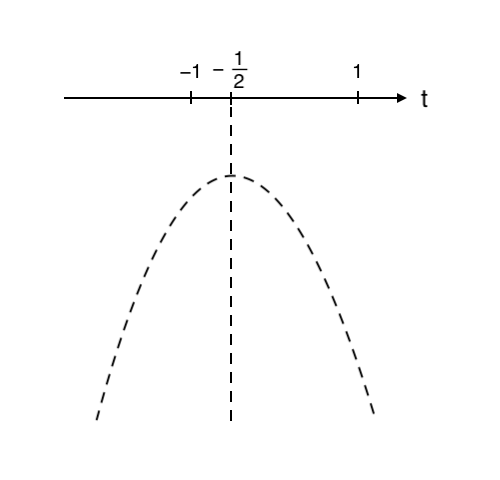
④ 放物線にプロットする

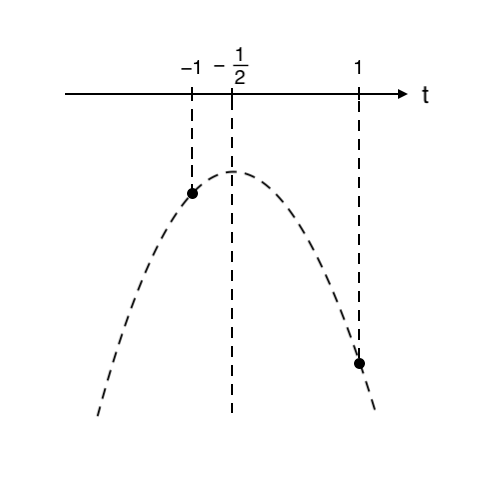
⑤ 範囲の部分を濃く塗る

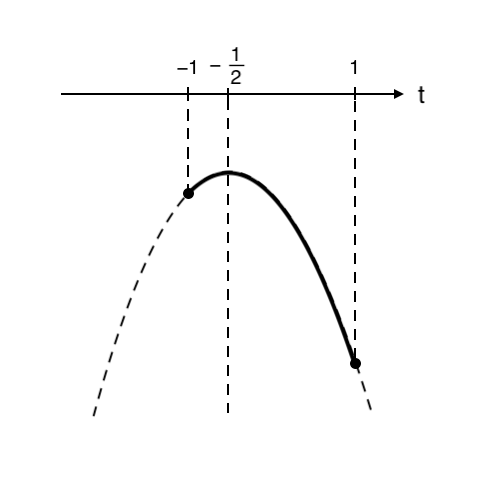
⑥ 高さが 最大・最小 の点を読み取る

 

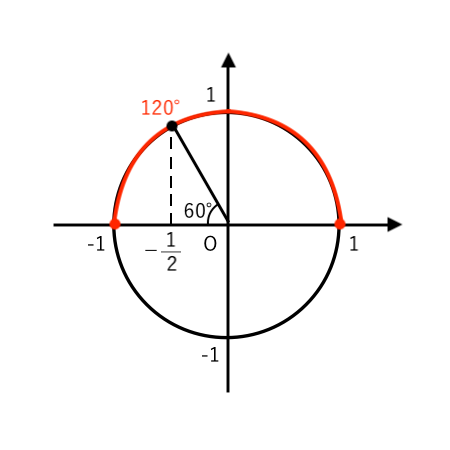
（注3）$ 0^\circ≦\theta≦180^\circ $ の範囲で

$ $　$ \cos \theta = −\displaystyle{1 \over 2} $

となるような $ \theta $ を考えると  $ \theta = 120^\circ $

 

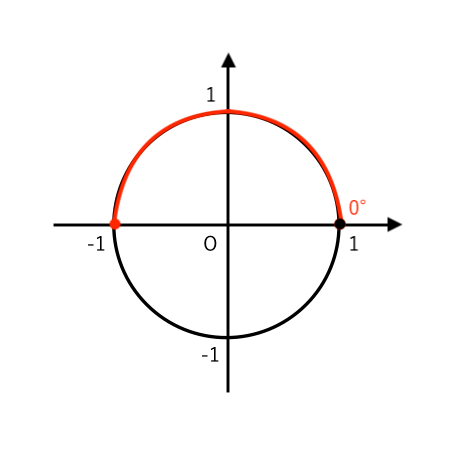
（注4）$ 0^\circ≦\theta≦180^\circ $ の範囲で

$ $　$ \cos \theta = 1 $

となるような $ \theta $ を考えると  $ \theta = 0^\circ $

Study more！２次関数の最大値・最小値

「２次関数の最大値・最小値の簡単な求め方（手抜きグラフ速答法）」はこちら。

関連記事

【２次関数】最大値と最小値の簡単な求め方【手抜きグラフで速答する裏ワザ】

２次関数の「最大値と最小値を求める問題」がよくわからない・・・ グラフを使ってどうやって求めればいいの？ ２次関数の最大値と最小値の簡単な求め方を教えてほしい！ こういった要望に応えます。   ２次関数の[…]

最後に

今回は「三角比の相互関係」の公式を使って解く応用問題を解説しました。

これらのパターンの問題は、学校のテスト でも 大学入試 でもよく出題されるので、何度も復習してスラスラ解けるようにしておきましょう！

質問・要望があれば気軽にコメントください👍