2次関数のグラフの頂点と軸はどうやって求めたらいいの?
2次関数の頂点・軸の公式は覚える必要があるの?
簡単に素早く求める方法を知りたい!
こういった疑問・要望にこたえます。
2次関数のグラフは 平方完成 をすると頂点・軸がわかるようになります。
2次関数 $y = a(x−p)^2 + q$ のグラフは
- 頂点 $(p, q)$
- 軸:$x = p$
今回は
- 2次関数の軸・頂点とは?
- 2次関数の軸・頂点の求め方
- 2次関数の平方完成のやり方
- 2次関数の軸・頂点を求める練習問題
を解説します。
【2次関数】グラフの頂点・軸とは?
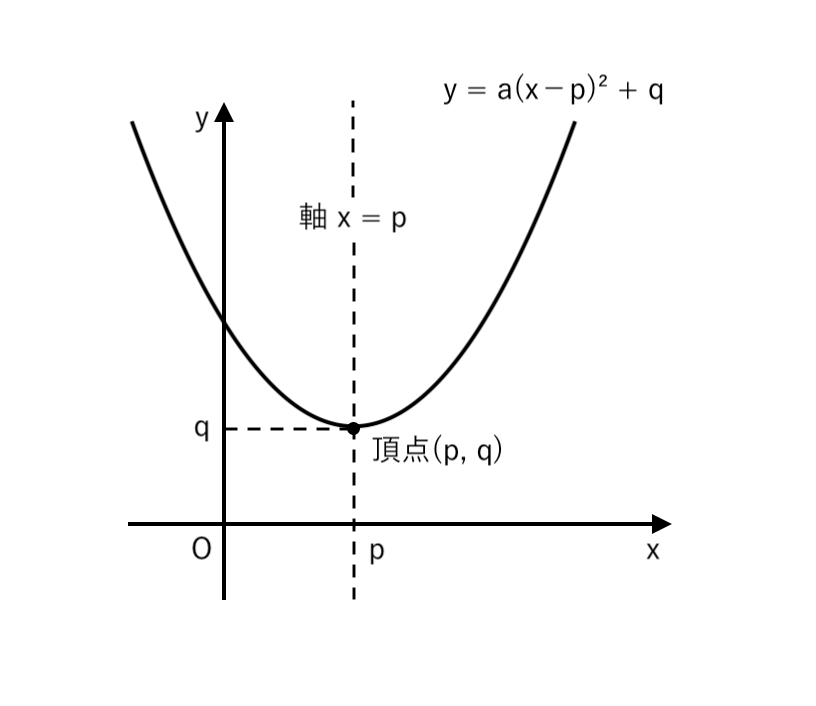
2次関数 $y = a(x−p)^2 + q$ について
- 頂点 $(p, q)$
- 軸:$x = p$
2次関数の頂点・軸の意味
2次関数 $y = a(x−p)^2 + q$ のグラフは
- 頂点 $(p, q)$ から上・下に 開く
- 軸:$x = p$ について 線対称(左右対称)
の放物線です。
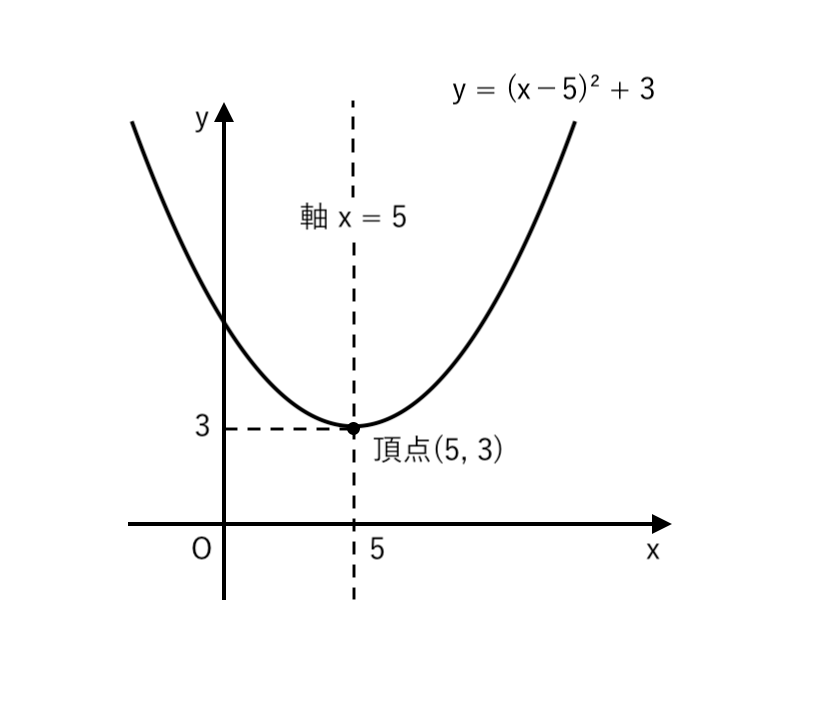
【例】2次関数 $y = (x−5)^2 + 3$ は
$ \begin{cases}
頂点 \enspace (5, 3) \\
\\
軸:x = 5 \\
\end{cases}$
より、下のようなグラフになることが分かりますね。
中学数学「2次関数 $y = ax^2$」と比較
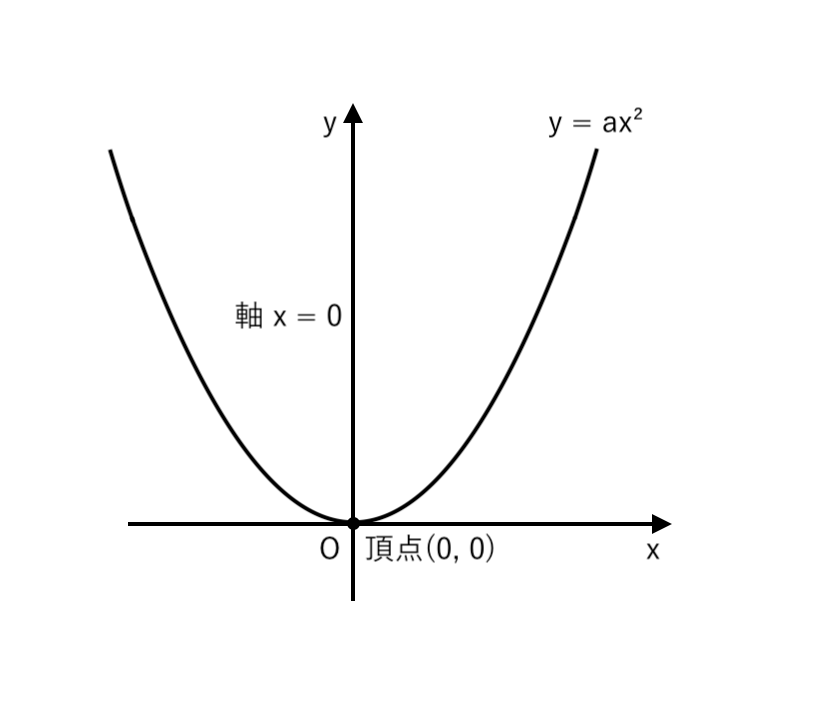
中学で習った2次関数「$y = ax^2$」のグラフを思い出しましょう。
$y = a(x−0)^2 + 0$ と変形できるので
$ \begin{cases}
頂点 (0, 0) \enspace ・・・ \enspace 原点O \\
\\
軸:x = 0 \enspace ・・・ \enspace y軸 \\
\end{cases}$
と見ることもできますね。
ということは、
2次関数「$y = a(x−\color{green}{p} )^2 + \color{red}{q}$ のグラフ」は「$y = ax^2$ のグラフ」を
$x$軸方向に $\color{green}{p}$、$y$軸方向に $\color{red}{q}$ だけ平行移動したもの
と考えることができます。
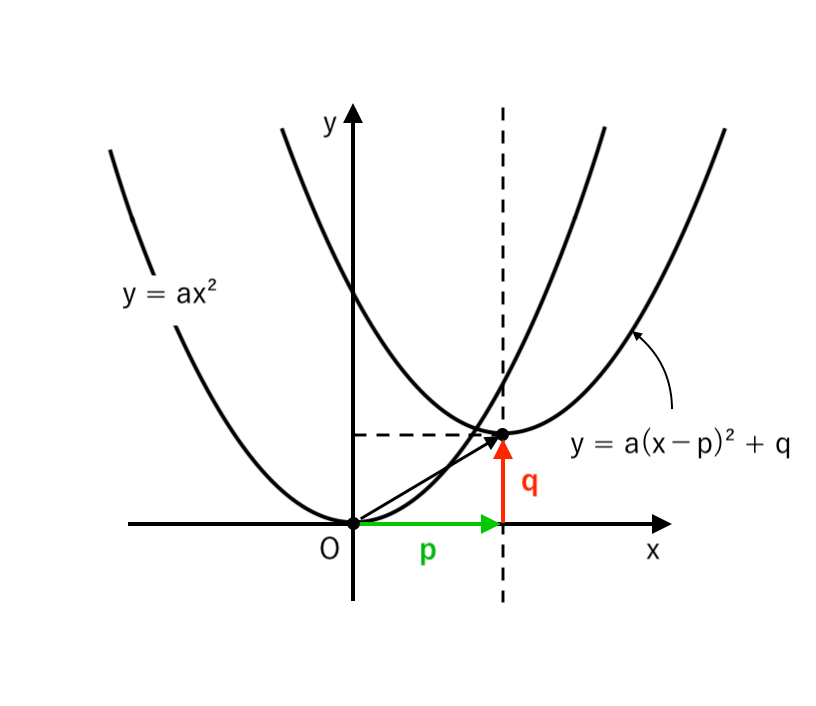
2次関数 $y = ax^2$ → $y = a(x−\color{green}{p} )^2 + \color{red}{q} $ に平行移動
$ \begin{cases}
頂点 (0, 0) \enspace → \enspace (\color{green}{p}, \color{red}{q} ) \\
\\
軸:x = 0 \enspace → \enspace x = \color{green}{p} \\
\end{cases}$
【2次関数】頂点・軸の求め方2つ:平方完成・公式
2次関数のグラフの頂点・軸の求め方 は2つあります。
- 平方完成 する ← オススメ!
- 公式を使う(非推奨)
結論から言うと、2次関数は「平方完成する」と覚えておけば大丈夫です。
全国の学校・塾(予備校)などでも、2次関数の頂点・軸を 公式 を使って求めるやり方はあまり指導されません。
理由は単純で「覚えにくい&使いにくい」からですね。
【2次関数】頂点・軸は平方完成でOK!
2次関数を「平方完成する」とは、
$ $ $\color{red}{ y = a(x−p)^2 + q } $
の形に変えることです。
平方完成することで、放物線の 頂点 と 軸 が分かるわけですね。
【例】
(1) $y = x^2 −6x + 5$
$ $ $= (x −3)^2 −3^2 + 5$
$ $ $= (x −3)^2 −4$
∴ $ \begin{cases}
頂点 \enspace (3, −4) \\
\\
軸:x = 3 \\
\end{cases}$
(2) $y = 2x^2 +12x + 7$
$ $ $= 2(x^2 +6x) + 7$
$ $ $= 2(x +3)^2 −3^2 \cdot 2 + 7$
$ $ $= 2(x +3)^2 −11$
∴ $ \begin{cases}
頂点 \enspace (−3, −11) \\
\\
軸:x = −3 \\
\end{cases}$
(3) $y = −2x^2 −6x −2 $
$ $ $= −2(x^2 +3x) −2 $
$ $ $\displaystyle { = −2\left( x +{3 \over 2} \right)^2 −{9 \over 4} \cdot (−2) −2 }$
$ $ $\displaystyle { = −2\left( x +{3 \over 2} \right)^2 +{5 \over 2} }$
∴ $ \begin{cases}
頂点 \enspace \displaystyle { \left(−{3 \over 2}, {5 \over 2} \right) } \\
\\
軸:\displaystyle { x = −{3 \over 2} } \\
\end{cases}$
2次関数の「平方完成 の簡単なやり方」はこちらに書いておきました。
学校や塾で教えられるような 普通の平方完成のやり方よりスピードが速い ので、ぜひマスターしておきましょう。
二次関数の「平方完成」の計算に手間取ったり、しかもミスをよくしてしまう 平方完成を素早く、確実に、簡単に計算する方法を知りたい! そもそもなぜ平方完成するの? 平方完成はいつ使うの? 今回の記事では、こういった悩み・疑問[…]
【2次関数】頂点・軸の公式は覚えなくていい
「2次関数の頂点・軸の公式を覚える必要があるのか?」という質問への答えですが、正直に言うと「公式は覚えなくていい」です。
なぜなら公式自体が覚えにくいのと、公式を使うとかえって計算スピードが遅くなってしまうから。
なので、ここでは軽い紹介にとどめておきます。
2次関数 $y = ax^2 + bx +c$ のグラフは
- 頂点 $ \displaystyle { \left(−{ b \over 2a}, −{ b^2 − 4ac \over 4a} \right) }$
- 軸:$ \displaystyle { x = −{ b \over 2a} }$
【例】2次関数 $y = 3x^2 + 2x +5$ のグラフは
・頂点 $ \displaystyle { \left( −{ 2 \over 2 \cdot 3 }, −{ 2^2 − 4 \cdot 3 \cdot 5 \over 4 \cdot 3} \right) }$
$ $ ∴ $ \displaystyle { \left( −{ 1 \over 3 }, { 14 \over 3} \right) }$
・軸:$ \displaystyle { x = −{ 2 \over 2 \cdot 3 } }$
$ $ $\displaystyle { = −{ 1 \over 3 } }$
公式にあてはめるだけですね。
ですが、公式が覚えにくかったり間違えやすいのでオススメはしません。
【2次関数】分数でくくる平方完成のやり方
$\displaystyle { y = \color{red}{2 \over 3}x^2 + 6x + 1}$ のように「$x^2$の係数が 分数」のときの 平方完成 についてはこちら。
分数でくくるタイプの平方完成がうまくできない・・・ x²の係数が分数のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 この記[…]
【2次関数】マイナスでくくる平方完成のやり方
$\displaystyle { y = \color{red}{−2}x^2 + 2x + 1}$ のように「$x^2$の係数が マイナス」のときの 平方完成 についてはこちら。
マイナスでくくるタイプの平方完成がうまくできない・・・ x²の係数がマイナス(負の値)のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 &nbs[…]
【2次関数】文字でくくる平方完成のやり方
$\displaystyle { y = \color{red}{a}x^2 + 2ax + 1}$ のように「$x^2$の係数が 文字」のときの 平方完成 についてはこちら。
aとかの文字(定数)でくくるタイプの平方完成がうまくできない・・・ x²の係数が文字(定数)のとき、くくり方がイマイチわからない どうやって平方完成すればいいのか分かりやすく教えてほしい! こういった要望に応えます。 &[…]
【2次関数】平方完成マスターのための練習問題
ここまでの内容がちゃんと理解できているか、練習問題を解いて確かめてみましょう!
【問題】次の2次関数を平方完成せよ。また、頂点の座標、軸の方程式を求めよ。
(1) $\displaystyle { y = x^2 −2x + 3 }$
(2) $\displaystyle { y = 3x^2 + 6x − 1 }$
(3) $\displaystyle { y = x^2 + 5x + 2 }$
(4) $\displaystyle { y = 5t^2 − 5t + 5 }$
(5) $\displaystyle { y = −x^2 − 4x + 3 }$
(6) $\displaystyle { y = −3x^2 − 4x − 1 }$
(7) $\displaystyle { y = {2 \over 3}x^2 − 2x + 4 }$
(8) $\displaystyle { y = −{4 \over 5}t^2 − 4t − 7 }$
(9) $\displaystyle { y = 2ax^2 − 10ax + 3a }$
(10) $\displaystyle { y = −{2 \over 3}ax^2 − 6ax − 12 a }$
- 【解答】を見る
- 【解答】
(1) $\displaystyle { y = \left(x −1 \right)^2 + 2 }$
$ $ 頂点$\displaystyle { \left( 1 , 2 \right) }$、軸 $\displaystyle { x = 1 }$(2) $\displaystyle { y = 3 \left(x + 1 \right)^2 −4 }$
$ $ 頂点$\displaystyle { \left( −1 , −4 \right) }$、軸 $\displaystyle { x = −1 }$(3) $\displaystyle { y = \left(x + {5 \over 2} \right)^2 −{17 \over 4} }$
$ $ 頂点$\displaystyle { \left( −{5 \over 2} , −{17 \over 4} \right) }$、軸 $\displaystyle { x = −{5 \over 2} }$(4) $\displaystyle { y = 5 \left( t − {1 \over 2} \right)^2 + {15 \over 4} }$
$ $ 頂点$\displaystyle { \left( {1 \over 2} , {15 \over 4} \right) }$、軸 $\displaystyle { t = {1 \over 2} }$(5) $\displaystyle { y = − \left(x + 2 \right)^2 + 7 }$
$ $ 頂点$\displaystyle { \left( −2 , 7 \right) }$、軸 $\displaystyle { x = −2 }$(6) $\displaystyle { y = −3 \left( x + {2 \over 3} \right)^2 +{1 \over 3} }$
$ $ 頂点$\displaystyle { \left( −{2 \over 3} , {1 \over 3} \right) }$、軸 $\displaystyle { x = −{2 \over 3} }$(7) $\displaystyle { y = {2 \over 3} \left( x − {3 \over 2} \right)^2 + {5 \over 2} }$
$ $ 頂点$\displaystyle { \left( {3 \over 2} , {5 \over 2} \right) }$、軸 $\displaystyle { x = {3 \over 2} }$(8) $\displaystyle { y = −{4 \over 5} \left( t + {5 \over 2} \right)^2 −2 }$
$ $ 頂点$\displaystyle { \left( −{5 \over 2} , −2 \right) }$、軸 $\displaystyle { t = −{5 \over 2} }$(9) $\displaystyle { y = 2a \left( x − {5 \over 2} \right)^2 − {19 \over 2} a }$
$ $ 頂点$\displaystyle { \left( {5 \over 2} , − {19 \over 2} a \right) }$、軸 $\displaystyle { x = {5 \over 2} }$(10) $\displaystyle { y = −{2 \over 3}a \left( x + {9 \over 2} \right)^2 + {3 \over 2} a }$
$ $ 頂点$\displaystyle { \left( −{9 \over 2} , {3 \over 2} a \right) }$、軸 $\displaystyle { x = −{9 \over 2} }$
- 【解説(計算過程)】を見る
- 【解説】
(1) $\displaystyle { x^2 −2x + 3 }$
$ $ $\displaystyle { = \left(x −1 \right)^2 −1 + 3 }$
$ $ $\displaystyle { = \left(x −1 \right)^2 + 2 }$
(2) $\displaystyle { 3x^2 + 6x − 1 }$
$ $ $\displaystyle { = 3 \left(x^2 + 2x \right) − 1 }$
$ $ $\displaystyle { = 3 \left(x + 1 \right)^2 −1 \cdot 3 − 1 }$
$ $ $\displaystyle { = 3 \left(x + 1 \right)^2 −4 }$
(3) $\displaystyle { x^2 + 5x + 2 }$
$ $ $\displaystyle { = \left(x + {5 \over 2} \right)^2 −{25 \over 4} + 2 }$
$ $ $\displaystyle { = \left(x + {5 \over 2} \right)^2 −{17 \over 4} }$
(4) $\displaystyle { 5t^2 − 5t + 5 }$
$ $ $\displaystyle { = 5 \left( t^2 − t \right) + 5 }$
$ $ $\displaystyle { = 5 \left( t − {1 \over 2} \right)^2 −{1 \over 4} \cdot 5 + 5 }$
$ $ $\displaystyle { = 5 \left( t − {1 \over 2} \right)^2 + {15 \over 4} }$
(5) $\displaystyle { −x^2 − 4x + 3 }$
$ $ $\displaystyle { = − \left(x^2 + 4x \right) + 3 }$
$ $ $\displaystyle { = − \left(x + 2 \right)^2 −4 \cdot (−1) + 3 }$
$ $ $\displaystyle { = − \left(x + 2 \right)^2 + 7 }$
(6) $\displaystyle { −3x^2 − 4x − 1 }$
$ $ $\displaystyle { =−3 \left( x^2 + {4 \over 3} x \right)− 1 }$
$ $ $\displaystyle { =−3 \left( x + {2 \over 3} \right)^2 −{4 \over 9} \cdot (−3)− 1 }$
$ $ $\displaystyle { =−3 \left( x + {2 \over 3} \right)^2 +{1 \over 3} }$
(7) $\displaystyle { {2 \over 3}x^2 − 2x + 4 }$
$ $ $\displaystyle { = {2 \over 3} \left( x^2 − 3x \right) + 4 }$
$ $ $\displaystyle { = {2 \over 3} \left( x − {3 \over 2} \right)^2 −{9 \over 4} \cdot {2 \over 3} + 4 }$
$ $ $\displaystyle { = {2 \over 3} \left( x − {3 \over 2} \right)^2 + {5 \over 2} }$
(8) $\displaystyle { −{4 \over 5}t^2 − 4t − 7 }$
$ $ $\displaystyle { = −{4 \over 5} \left( t^2 + 5t \right) − 7 }$
$ $ $\displaystyle { = −{4 \over 5} \left( t + {5 \over 2} \right)^2 −{25 \over 4} \cdot \left(−{4 \over 5} \right) − 7 }$
$ $ $\displaystyle { = −{4 \over 5} \left( t + {5 \over 2} \right)^2 −2 }$
(9) $\displaystyle { 2ax^2 − 10ax + 3a }$
$ $ $\displaystyle { = 2a \left( x^2 − 5x \right) + 3a }$
$ $ $\displaystyle { = 2a \left( x − {5 \over 2} \right)^2 − {25 \over 4} \cdot 2a + 3a }$
$ $ $\displaystyle { = 2a \left( x − {5 \over 2} \right)^2 − {19 \over 2} a }$
(10) $\displaystyle { −{2 \over 3}ax^2 − 6ax −12 a }$
$ $ $\displaystyle { = −{2 \over 3}a \left( x^2 + 9x \right) − 12 a }$
$ $ $\displaystyle { = −{2 \over 3}a \left( x + {9 \over 2} \right)^2 −{81 \over 4} \cdot \left(−{2 \over 3}a \right) − 12 a }$
$ $ $\displaystyle { = −{2 \over 3}a \left( x + {9 \over 2} \right)^2 + {3 \over 2} a }$
最後に
どうでしたか? 2次関数の平方完成には慣れましたか?
平方完成は、2次関数のほかにも様々な問題を解くうえで必要になります。
いつでもスラスラ計算できるように、たくさん練習しておきましょう!
2次関数のグラフの簡単な書き方(裏ワザ)
2次関数のグラフを「簡単に」「素早く」「キレイに」書く裏ワザ についてはこちら。
2次関数のグラフ(放物線)がフリーハンドでうまく書けない・・・ 放物線をキレイに見やすく書くのって難しいな〜 2次関数のグラフの簡単な書き方・裏ワザを教えてほしい! こういった要望に応えます。 実は「[…]
質問・要望があれば気軽にコメントください👍