「2次関数の最大値・最小値を求める問題」で場合分けが3つになるパターンがよく分からない・・・
どうやって 3つに場合分けしたらいいの?
教科書や学校の授業だとよく理解できないから、わかりやすく解説してほしい!
こういったお悩みを解決します。
2次関数で場合分けが必要な問題 は、学校のテストや大学入試でもよく出るので
しっかり解けるようにしておかなければいけません。
にも関わらず、教科書や学校の授業は説明が分かりにくいために「2次関数の場合分けがニガテだ・・・」という高校生・受験生はたくさんいます。
このページを読めば、
「2次関数の最大値・最小値を求める問題」で場合分けが 3つ になるパターンの解き方がスッキリ分かります。
できる限り「丁寧」かつ「シンプルに」分かりやすく説明していきます!
【2次関数】場合分けが「3つ」のパターン【最大値・最小値の求め方】
「2次関数の最大値・最小値を求める問題」の場合分けのポイントは
によって場合分けするということです。
さらに、その中でも
- 下に凸 × 最大値
- 上に凸 × 最小値
のパターンの問題で場合分けに必要なのが
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
2次関数が「下に凸」「上に凸」のパターンに分けてそれぞれ解説していきます。
【2次関数】場合分けが「3つ」のパターン(下に凸)

まずは「2次関数(下に凸)の最大値・最小値を求める問題」から見ていきましょう。
【パターン1】下に凸 × 最大値
「下に凸 × 最大値」のパターンは、以下の3つに場合分けできます。
$ $[1] 最大値が「左」(中<軸)
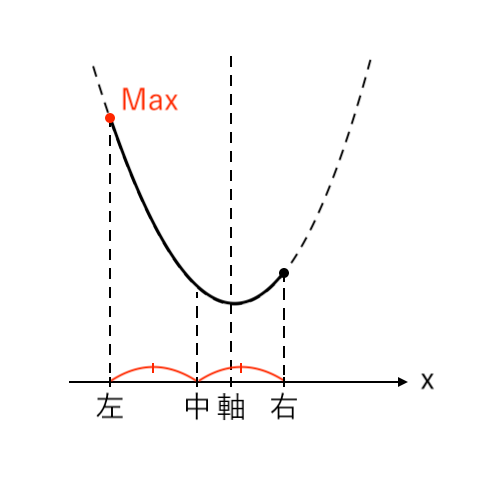
$ $[2] 最大値が「左・右」(軸=中)
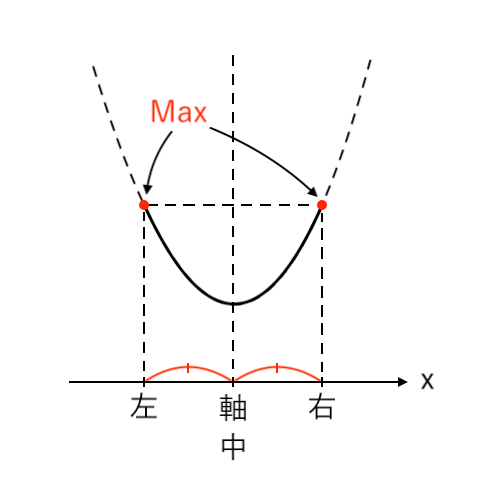
$ $[3] 最大値が「右」(軸<中)
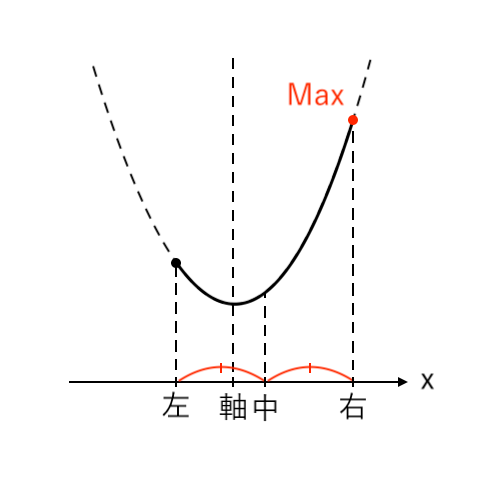
実際の問題で解説していきます!
まずは平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ y = x^2 -2ax + a^2 + 1 $
$ $ $ = (x -a)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (a, 1) \\
\\
軸:x = a \\
\\
下に凸 \\
\end{cases}$ の放物線。
定数aの値によって軸の位置が変わるので、場合分けをしなければいけません。
さて、ここで場合分けに必要なのが
ここで、$0≦x≦2$ における中央の値は
$ $ $ \displaystyle{ { 0 + 2 \over 2 } = 1 } $
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
最大値(グラフ上で一番高いところ)が「左」「頂点」「右」のどこになるか?を考えると
下に凸のグラフなので、最大値が「頂点」の場合はありえませんね。
なので、以下の3つに場合分けします。
$ $[1] 最大値が「左」(中<軸)
$ $[2] 最大値が「左・右」(軸=中)
$ $[3] 最大値が「右」(軸<中)
[1] 最大値が「左」(中<軸)
最大値をとるような $x$ の値が「左($x=0$)」の場合を考えます。
このとき、「中<軸」より「$1<a$」です。
簡単なグラフの書き方は、以下の手順になります。
① $x$軸、下に凸の放物線、放物線の軸 を用意する
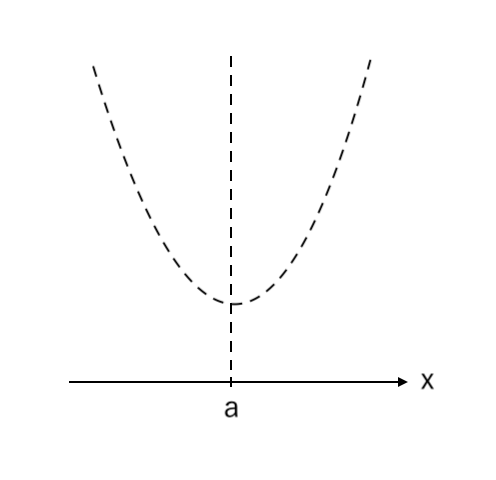
② 中<軸 となるように「中($x=1$)」を書く
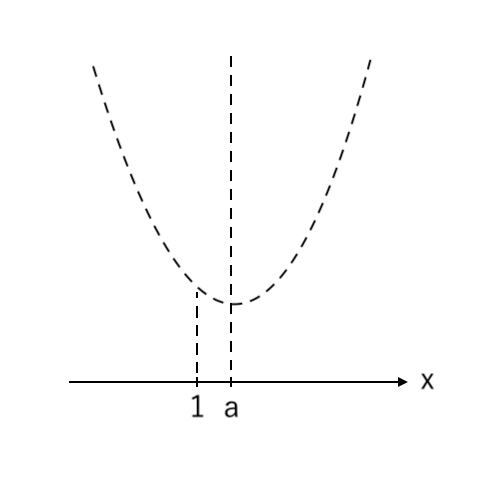
③ 左右のバランスを考えながら「左($x=0$)」「右($x=2$)」を書く
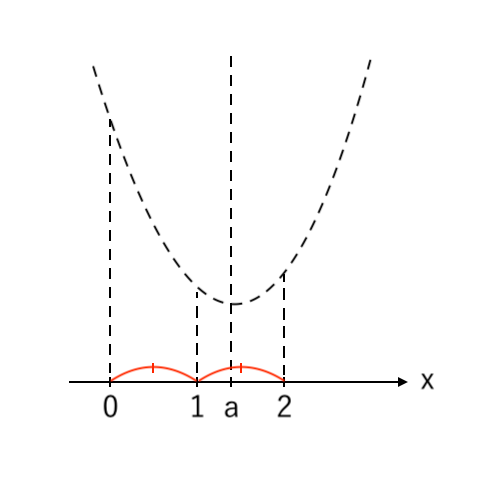
③ 放物線にプロットして、範囲を濃く塗る
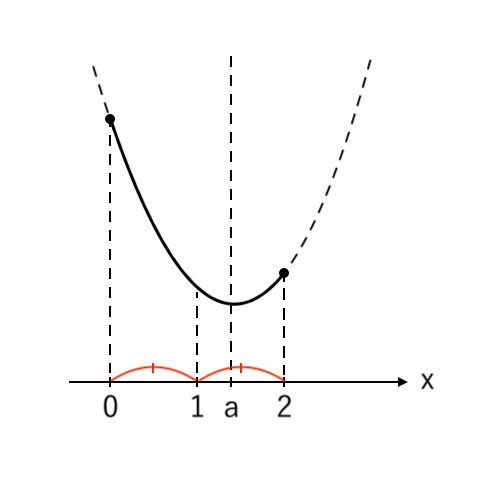
④ 高さが最大の点を読み取る
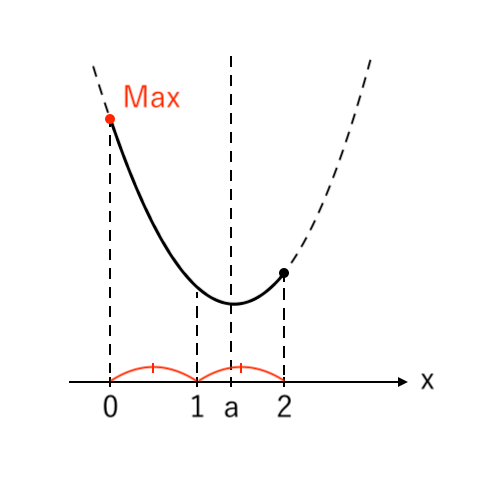
こんな感じです。
なので、[1]の場合 の解答は以下の通り。
$ $[1] $1<a$ のとき
$ $ $x = 0$ で 最大値 $a^2+1$
あとは、同じ要領で [2]、[3]の場合 も考えればOK!
[2] 最大値が「左・右」(軸=中)
最大値をとるような $x$ の値が「左($x=0$)」と「右($x=2$)」の場合(左・右の高さが揃う)を考えます。
このとき、軸と「中」が重なっているので、
「軸=中」より「$a=1$」ですね。
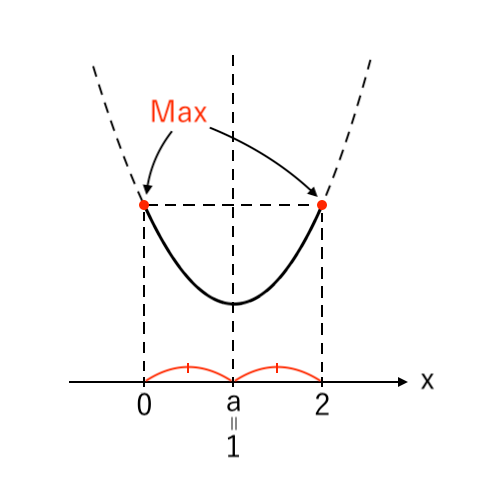
$ $[2] $a=1$ のとき
$ $ $ x=0, 2 $ で 最大値 $a^2 + 1 = 2 $ ($a=1$ を代入)
[3] 最大値が「右」(軸<中)
最大値をとるような $x$ の値が「右($x=2$)」の場合を考えます。
このとき、「軸<中」より「$a<1$」です。
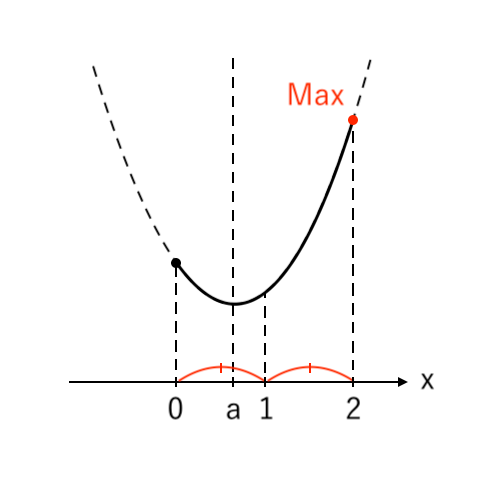
$ $[3] $a<1$ のとき
$ $ $x=2$ で 最大値 $a^2-4a+5$
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = x^2 -2ax + a^2 + 1 $
$ $ $ = (x -a)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (a, 1) \\
\\
軸:x = a \\
\\
下に凸 \\
\end{cases}$ の放物線。ここで、$0≦x≦2$ における中央の値は
$ $ $ \displaystyle{ { 0 + 2 \over 2 } = 1 } $
よって、以下の3つに場合分けできる。
$ $[1] $1<a$ のとき

$ $ $x = 0$ で 最大値 $a^2+1$
$ $[2] $a=1$ のとき

$ $ $ x=0, 2 $ で 最大値 $a^2 + 1 = 2 $ ($a=1$ を代入)
$ $[3] $a<1$ のとき

$ $ $x=2$ で 最大値 $a^2-4a+5$
$ $[1]〜[3]より、求める最大値は
$ \begin{cases}
1<a \enspace のとき \enspace \enspace a^2+1 \enspace (x = 0) \\
\\
a=1 \enspace のとき \enspace \enspace 2 \enspace (x=0, 2) \\
\\
a<1 \enspace のとき \enspace \enspace a^2-4a+5 \enspace (x = 2) \\
\end{cases}$
【パターン2】下に凸 × 最小値
次は「下に凸 × 最小値」のパターンです。
以下の3つに場合分けできます。
$ $[1] 最小値が「右」(右<軸)
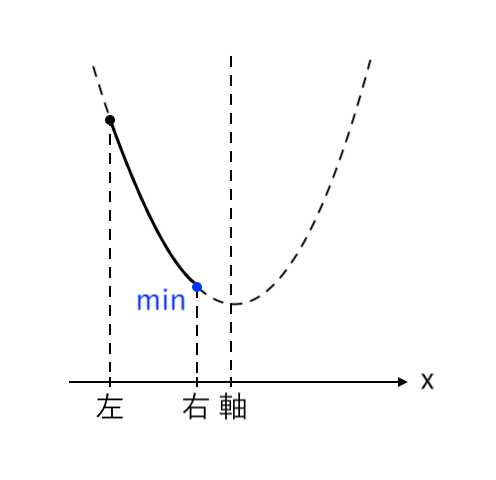
$ $[2] 最小値が「頂点」(左≦軸≦右)
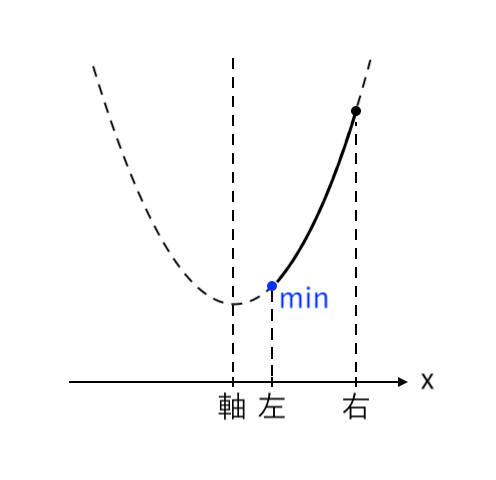
$ $[3] 最小値が「左」(軸<左)
実際の問題で解説していきます!
まずは平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ y = x^2 -2ax + a^2 + 1 $
$ $ $ = (x -a)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (a, 1) \\
\\
軸:x = a \\
\\
下に凸 \\
\end{cases}$ の放物線。
ここまではさっきの「例題1」と同じ流れです。
最小値(グラフ上で一番低いところ)が「左」「頂点」「右」のどこになるか?を考えると
以下の3つに場合分けできます。
$ $[1] 最小値が「右」(右<軸)
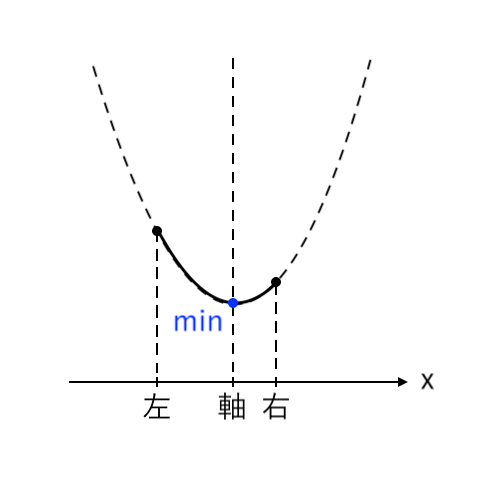
$ $[2] 最小値が「頂点」(左≦軸≦右)
$ $[3] 最小値が「左」(軸<左)
[1] 最小値が「右」(右<軸)
最小値をとるような $x$ の値が「右($x=2$)」の場合を考えます。
このとき、「右<軸」より「$2<a$」です。
簡単なグラフの書き方は、以下の手順になります。
① $x$軸、下に凸の放物線、放物線の軸 を用意する

② 右<軸 となるように「右($x=2$)」を書く
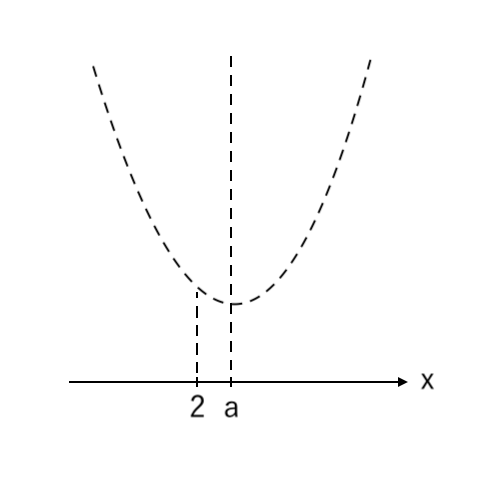
③ 「左($x=0$)」を書く
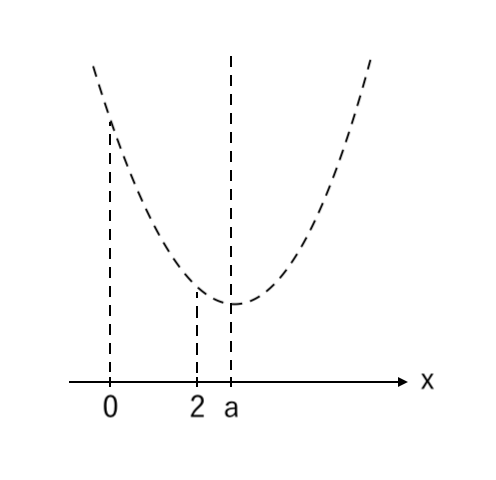
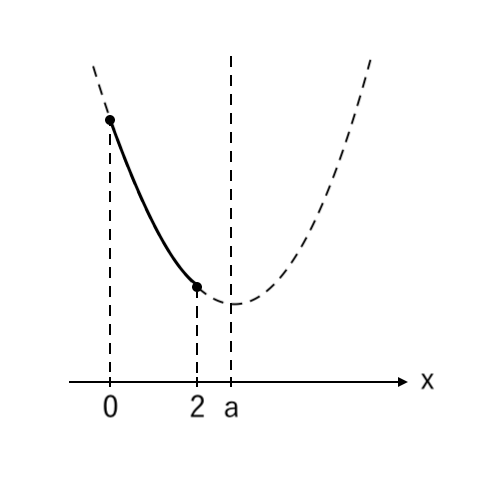
③ 放物線にプロットして、範囲を濃く塗る
④ 高さが最小の点を読み取る
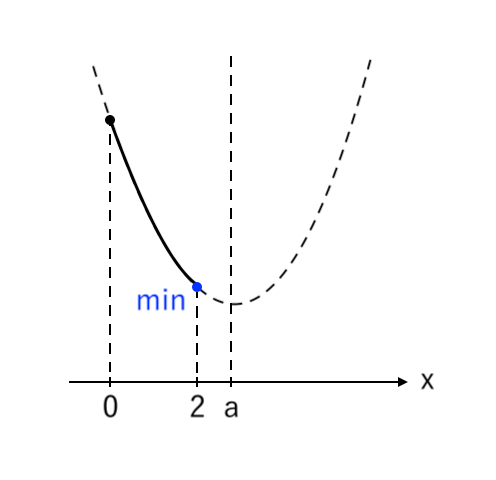
よって、[1]の場合 の解答は以下の通り。
$ $[1] $2<a$ のとき
$ $ $x = 2$ で 最小値 $a^2 -4a +5$
あとは、同じ要領で [2]、[3]の場合 も考えればOK!
[2] 最小値が「頂点」(左≦軸≦右)
最小値をとるような $x$ の値が「頂点($x=a$)」の場合を考えます。
このとき、「左≦軸≦右」より「$0≦a≦2$」です。
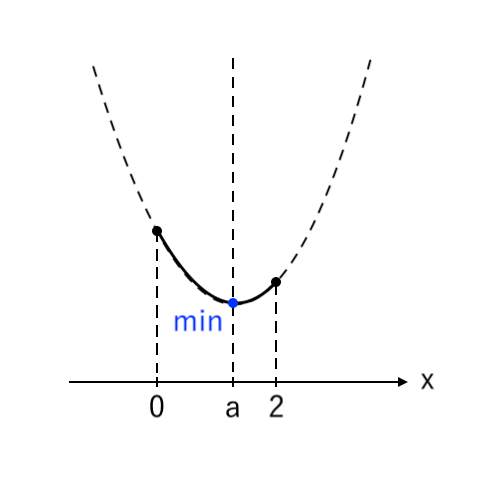
$ $[2] $ 0≦a≦2 $ のとき
$ $ $ x = a $ で 最小値 $ 1 $
[3] 最小値が「左」(軸<左)
最小値をとるような $x$ の値が「左($x=0$)」の場合を考えます。
このとき、「軸<左」より「$a<0$」です。
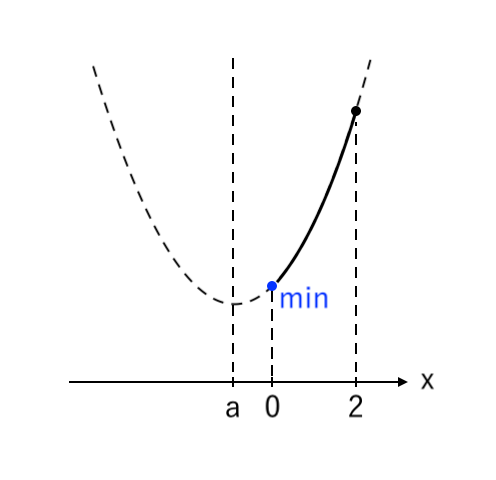
$ $[3] $ a<0 $ のとき
$ $ $ x = 0 $ で 最小値 $ a^2 + 1 $
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = x^2 -2ax + a^2 + 1 $
$ $ $ = (x -a)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (a, 1) \\
\\
軸:x = a \\
\\
下に凸 \\
\end{cases}$ の放物線。$ $[1] $2<a$ のとき

$ $ $x = 2$ で 最小値 $ a^2 -4a +5 $
$ $[2] $ 0≦a≦2 $ のとき

$ $ $ x = a $ で 最小値 $ 1 $
$ $[3] $ a<0 $ のとき

$ $ $ x = 0 $ で 最小値 $ a^2 + 1 $
$ $[1]〜[3]より、求める最小値は
$ \begin{cases}
2<a \enspace のとき \enspace \enspace a^2 -4a +5 \enspace (x = 2) \\
\\
0≦a≦2 \enspace のとき \enspace \enspace 1 \enspace (x=a) \\
\\
a<0 \enspace のとき \enspace \enspace a^2 + 1 \enspace (x = 0) \\
\end{cases}$
補足:場合分けでイコールをどっちにつければいいの?
2次関数の場合分けを生徒に教えているときに、よくある質問が

$ $[2] $0≦a≦2$ のとき ってどうして「$0\color{red}{<}a\color{red}{<}2$」じゃなくて「$0 \color{red}{≦}a\color{red}{≦}2$」ってイコールが入ってるの?
$ $[1] $ 2 \color{red}{<}a $ → $ $[1] $ 2\color{red}{≦}a $
$ $[3] $ a \color{red}{<}0 $ → $ $[3] $ a\color{red}{≦}0 $
みたいに[1]と[3]の場合分けにイコールを入れちゃダメなの?
というものです。
これに対する答えは「漏れやダブりがなければ、どっちにイコールを入れてもOK!」です。
なので、
$ $ [1] $ 2 \color{red}{≦}a $
$ $ [2] $0 \color{red}{<} a \color{red}{<} 2$
$ $ [3] $ a \color{red}{≦}0 $
のように場合分けしても全く問題ありません。
【2次関数】場合分けが「3つ」のパターン(上に凸)

次は「2次関数(上に凸)の最大値・最小値を求める問題」を解説していきます。
【パターン3】上に凸 × 最大値
「上に凸 × 最大値」のパターンは、以下の3つに場合分けできます。
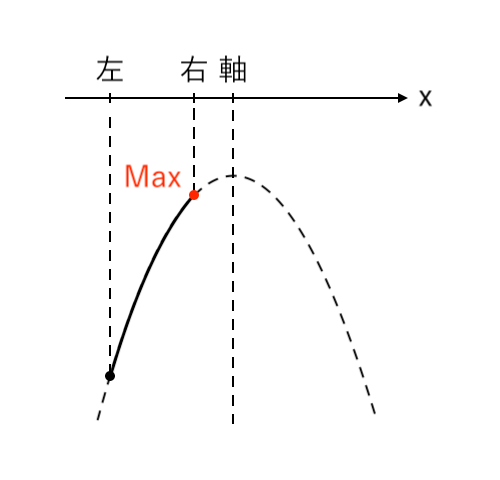
$ $[1] 最大値が「右」(右<軸)
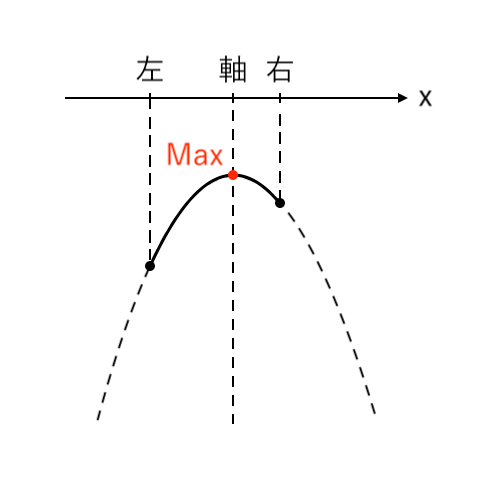
$ $[2] 最大値が「頂点」(左≦軸≦右)
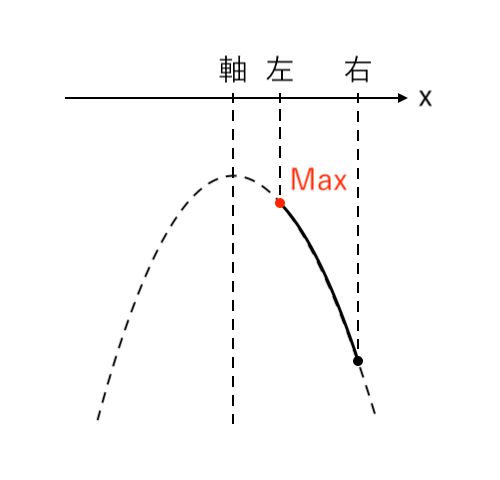
$ $[3] 最大値が「左」(軸<左)
実際の問題を見ていきましょう!
まずは平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ y = -x^2 +2ax -a^2 -1 $
$ $ $ = -(x -a)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (a, -1 ) \\
\\
軸:x = a \\
\\
上に凸 \\
\end{cases}$ の放物線。
最大値(グラフ上で一番高いところ)が「左」「頂点」「右」のどこになるか?を考えると
以下の3つに場合分けできます。
$ $[1] 最大値が「右」(右<軸)
$ $[2] 最大値が「頂点」(左≦軸≦右)
$ $[3] 最大値が「左」(軸<左)
[1] 最大値が「右」(右<軸)
最大値をとるような $x$ の値が「右($x=2$)」の場合を考えます。
このとき、「右<軸」より「$2<a$」です。
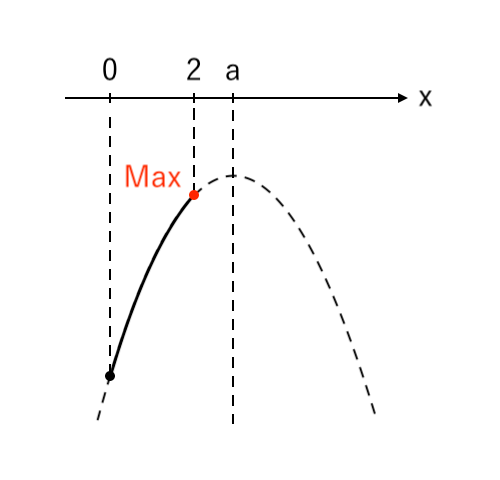
$ $[1] $2<a$ のとき
$ $ $x = 2$ で 最大値 $-a^2 +4a -5$
[2] 最大値が「頂点」(左≦軸≦右)
最大値をとるような $x$ の値が「頂点($x=a$)」の場合を考えます。
このとき、「左≦軸≦右」より「$0≦a≦2$」です。
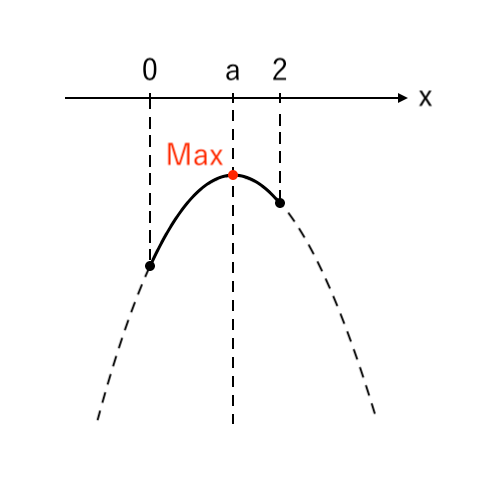
$ $[2] $0≦a≦2$ のとき
$ $ $x = a$ で 最大値 $-1$
[3] 最大値が「左」(軸<左)
最大値をとるような $x$ の値が「左($x=0$)」の場合を考えます。
このとき、「軸<左」より「$a<0$」です。
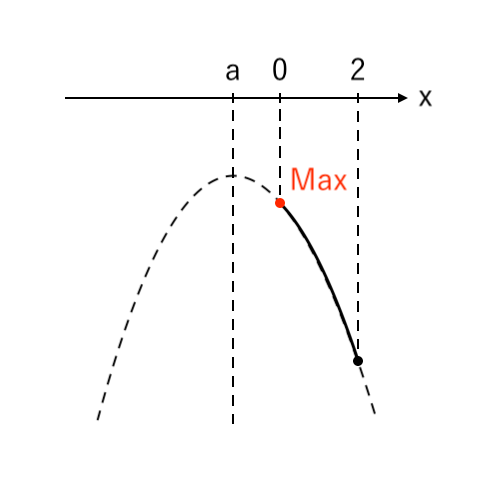
$ $[3] $a<0$ のとき
$ $ $x = 0$ で 最大値 $-1$
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = -x^2 +2ax -a^2 -1 $
$ $ $ = -(x -a)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (a, -1 ) \\
\\
軸:x = a \\
\\
上に凸 \\
\end{cases}$ の放物線。$ $[1] $2<a$ のとき

$ $ $x = 2$ で 最大値 $-a^2 +4a -5$
$ $[2] $0≦a≦2$ のとき

$ $ $x = a$ で 最大値 $-1$
$ $[3] $a<0$ のとき

$ $ $x = 0$ で 最大値 $-1$
$ $[1]〜[3]より、求める最大値は
$ \begin{cases}
2<a \enspace のとき \enspace \enspace -a^2 +4a -5 \enspace (x = 2) \\
\\
0≦a≦2 \enspace のとき \enspace \enspace -1 \enspace (x=a) \\
\\
a<0 \enspace のとき \enspace \enspace -a^2 – 1 \enspace (x = 0) \\
\end{cases}$
【パターン4】上に凸 × 最小値
「上に凸 × 最小値」のパターンは、以下の3つに場合分けできます。
$ $[1] 最小値が「左」(中<軸)
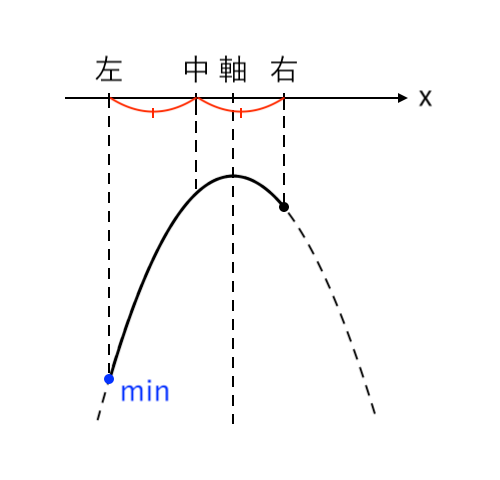
$ $[2] 最小値が「左・右」(軸=中)
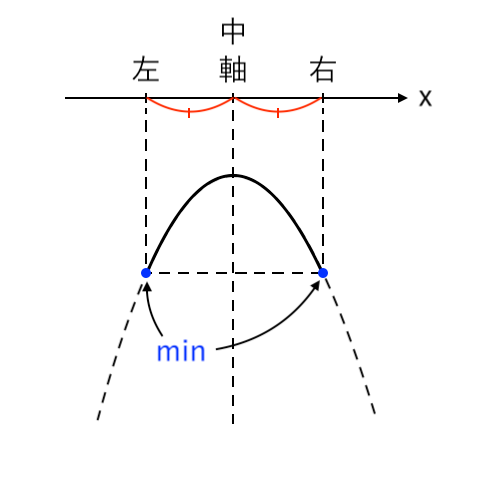
$ $[3] 最小値が「右」(軸<中)
実際の問題で解説していきます!
まずは平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ $ $ y = -(x -a)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (a, -1 ) \\
\\
軸:x = a \\
\\
上に凸 \\
\end{cases}$ の放物線。
さて、ここで場合分けをするのに必要なのが
ここで、$0≦x≦2$ における中央の値は
$ $ $ \displaystyle{ { 0 + 2 \over 2 } = 1 } $
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
最小値(グラフ上で一番低いところ)が「左」「頂点」「右」のどこになるか?を考えると
上に凸のグラフなので、最小値が「頂点」の場合はありえませんね。
なので、以下の3つに場合分けします。
$ $[1] 最小値が「左」(中<軸)
$ $[2] 最小値が「左・右」(軸=中)
$ $[3] 最小値が「右」(軸<中)
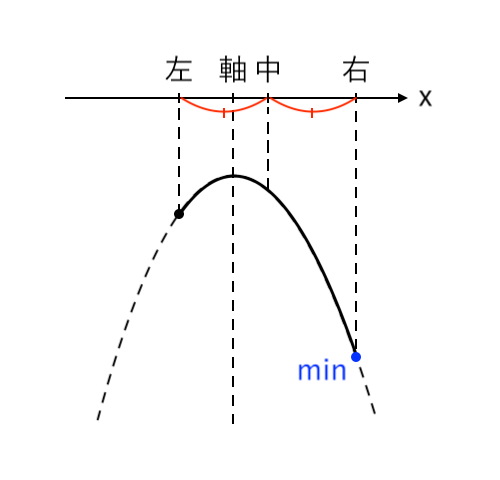
[1] 最小値が「左」(中<軸)
最小値をとるような $x$ の値が「左($x=0$)」の場合を考えます。
このとき、「中<軸」より「$1<a$」です。
$ $[1] $1<a$ のとき
$ $ $x = 0$ で 最小値 $-a^2-1$
[2] 最小値が「左・右」(軸=中)
最小値をとるような $x$ の値が「左($x=0$)」と「右($x=2$)」の場合(左・右の高さが揃う)を考えます。
このとき、軸と「中」が重なっているので、
「軸=中」より「$a=1$」となります。
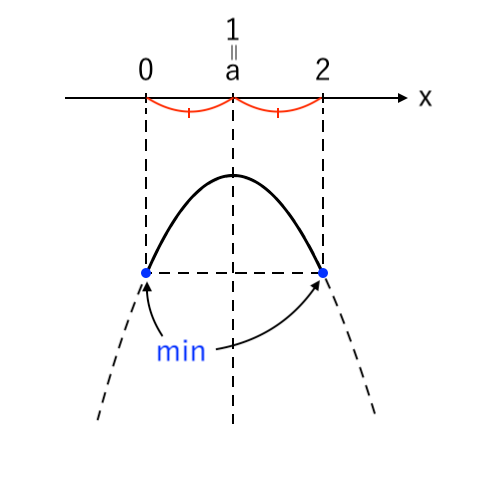
$ $[2] $a=1$ のとき
$ $ $ x=0, 2 $ で 最小値 $-a^2 – 1 = -2 $ ($a=1$ を代入)
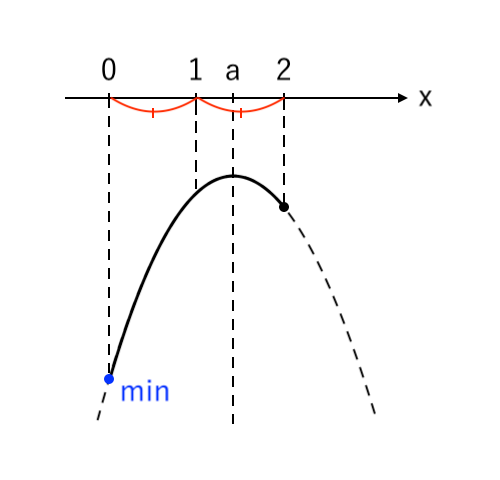
[3] 最小値が「右」(軸<中)
最小値をとるような $x$ の値が「右($x=2$)」の場合を考えます。
このとき、「軸<中」より「$a<1$」です。
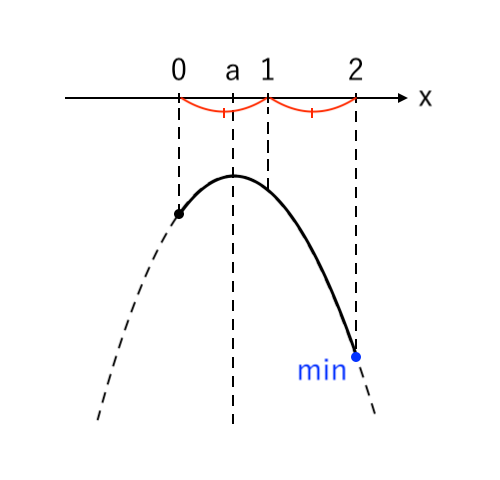
$ $[3] $a<1$ のとき
$ $ $x=2$ で 最小値 $-a^2 +4a -5$
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ $ $ y = -(x -a)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (a, -1 ) \\
\\
軸:x = a \\
\\
上に凸 \\
\end{cases}$ の放物線。ここで、$0≦x≦2$ における中央の値は
$ $ $ \displaystyle{ { 0 + 2 \over 2 } = 1 } $
よって、以下の3つに場合分けできる。
$ $[1] $1<a$ のとき

$ $ $x = 0$ で 最小値 $-1$
$ $[2] $a=1$ のとき

$ $ $ x=0, 2 $ で 最小値 $-a^2 – 1 = -2 $ ($a=1$ を代入)
$ $[3] $a<1$ のとき

$ $ $x=2$ で 最小値 $-a^2 +4a -5$
$ $[1]〜[3]より、求める最小値は
$ \begin{cases}
1<a \enspace のとき \enspace \enspace -a^2-1 \enspace (x = 0) \\
\\
a=1 \enspace のとき \enspace \enspace -2 \enspace (x=0, 2) \\
\\
a<1 \enspace のとき \enspace \enspace -a^2 +4a -5 \enspace (x = 2) \\
\end{cases}$
以上です。お疲れ様でした!
【まとめ】2次関数の場合分けが「3つ」のパターン【最大値・最小値の求め方】
最後にまとめです。
「2次関数の最大値・最小値を求める問題」の場合分けのポイントは
中でも
- 下に凸 × 最大値
- 上に凸 × 最小値
のパターンの問題で場合分けをするときに必要なのが
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
似たような問題をたくさん解いて、2次関数の場合分けに慣れておきましょう!
【2次関数】最大値と最小値の簡単な求め方(手抜きグラフ速答法)
2次関数の「最大値と最小値を求める問題」がよくわからない・・・ グラフを使ってどうやって求めればいいの? 2次関数の最大値と最小値の簡単な求め方を教えてほしい! こういった要望に応えます。 2次関数の[…]
質問・要望があれば気軽にコメントください👍