この記事では、絶対値記号のついた等式・不等式の解き方 を解説します。
絶対値の問題は等式・不等式で解き方が変わったり、場合分け が必要になったりするので意外とつまづく生徒が多いです。
|x| = 5 を解くと、どうして x = ± 5 みたいに解が2つ出てくるの?
|x−2| < 5 だと場合分けしないのに、どうして |x−2| < 3x だと場合分けするの?
そもそも場合分けのやり方とか意味がよくわからない!
こういった疑問をお持ちであれば、ぜひこのページを最後まで読んでみてください。
スッキリ解消されて、絶対値の問題 を悩むことなく解けるようになります。
丁寧に書いているので、人によっては回りくどく感じる部分もあるかもしれません。
分かるところは飛ばしながら読んでいただいても大丈夫です。
絶対値とは?
さて、まずは絶対値のおさらいです。
絶対値 とは、ひとことで言えば
原点Oからの距離
です。
ポイントは、「距離」なのでその値は 必ず「0以上(0またはプラス)」になる ということです。
(例えば「家から学校までの距離がマイナス500m」なんて言わないですよね?なので、距離は常に0以上です)
絶対値の計算では、絶対値の中身が「0以上(0・正)」か「マイナス(負)」かによって、2通りに分けられます。
まずは絶対値の中身が「0以上」の場合を見てみましょう。
【例題0-1】 |5| の値を求めよ。
|5| は「絶対値5」とか「5の絶対値」とか言います。
原点Oからどれだけ離れているか(距離)が絶対値なので、
となります。
数直線で表すと、
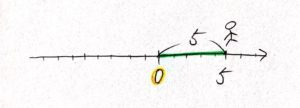
緑色の部分が「原点Oから5までの距離」を表しています。
つまり、絶対値の中身が「0以上」のときは、符号そのままで絶対値を外す!
【補足】
【例題0-2】 |−5| の値を求めよ。
次に、|−5| を考えます。
|−5| は、原点Oから−5までの距離なので、
になります。
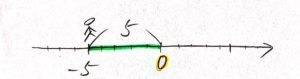
絶対値の中身がマイナス(負の数)のときは、絶対値を外すときに符号を変えてプラス(正の数)にします。
つまり、符号を逆にして絶対値を外す!
まとめ
ここまでの内容をまとめましょう。
[2] $x \color{blue}{< 0} $ のとき $|x| = −x$ (符号を逆に)
ここまで理解できたら準備はOKです。
さっそく次に進みましょう!
【パターン1】絶対値の等式 |x| = 5 の解き方
ここから本題に入ります。
まずは、絶対値のついた等式 の問題から見ていきましょう。
【例題1-1】 $|x| = 5$ を解け。
解答は以下のようにまとめて書いて大丈夫です。
$|x| = a$ を解くと $x = \pm a$
【例題1-2】 $|x−2| = 5$ を解け。
【パターン2】絶対値の不等式 |x| < 5 の解き方
次に、絶対値のついた不等式(<, >, ≦, ≧)の解き方を説明します。
【例題2-1】 $|x| < 5$ を解け。
まずは、「小なり(<)」や「小なりイコール(≦)」がついた不等式です。
となります。
解答は以下だけでOK。
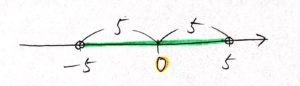
$|x| < a$ を解くと $−a < x < a$
$|x| ≦ a$ を解くと $−a ≦ x ≦ a$
【例題2-2】 $|x| ≧ 5$ を解け。
今度は、「大なり(>)」や「大なりイコール(≧)」の場合です。
$|x| > a$ を解くと $x<−a, \enspace a < x$
$|x| ≧ a$ を解くと $x≦−a, \enspace a ≦ x$
【例題2-3】 $|x − 2| ≦ 5$ を解け。
では、絶対値の中身が「$x − 2$」のようになった場合はどうなるでしょうか?
やはり、
のように、絶対値の中身をかたまりと見なします。
例題2-1の「まとめ(簡便法)」より、
【例題2-4】 $|x − 2| ≧ 5$ を解け。
例題2-2の「まとめ(簡便法)」より、
【パターン3】絶対値の等式 |x−2| = 3x の解き方
次は「絶対値の 外に変数($x$など)がある」「等式」のパターンです。
(変数は、ここでいうと右辺の $3x$)
このパターンでは原則 場合分けが必要 になります。
記述式であれば、場合分けは「解答」としてしっかり書きましょう。
【例題3】 $|x − 2| = 3x$ を解け。
絶対値の中身($x − 2$)が「0以上」か「マイナス」かで 2つに場合分けします。
(注)出てきた解が条件を満たすか、必ず確かめること!(確かめがないと減点されます)
逆に条件を満たさなければ
と書くとスッキリしておすすめ。
【別解】簡便法
さて、このパターンは上記のように原則として場合分けをしますが、実は以下のように 簡便法 を使うこともできます。
- 【別解】を見る
-
【別解】
$(左辺)= |x − 2| \color{red}{≧ 0} $ より
$ $ $ (右辺)= 3x \color{red}{≧ 0} $
∴ $ x ≧ 0 $
このとき
$ $ $ x − 2 = \pm 3x $
∴ $ 2x = − 2 \ または \ 4x = 2 $
∴ $ x = − 1 \ または \ \displaystyle {x = {1\over2}} $
$ x ≧ 0 $ より $\displaystyle {x = {1\over2}} $
こちらの【別解】の方がスッキリ書けますが、後々「絶対値を含む関数(例:$y = |x^2 + 3x + 2| – 5x+3$ )」を扱う際に、場合分けをする必要があるので、【解答】のやり方もできるようにしておきましょう!
【パターン4】絶対値の不等式 |x−2| < 3x の解き方
「絶対値の 外に変数($x$など)がある」「不等式」のパターンです。
このパターンでも原則として場合分けが必要です。
先ほどの問題は等式だったので、解がズバリ「値」で出てきましたが、今回は不等式のため「範囲」が答えになります。
【例題4】 $|x − 2| < 3x$ を解け。
(注1)共通範囲をとる
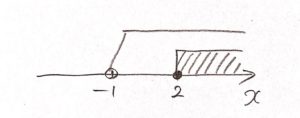
(注2)共通範囲をとる
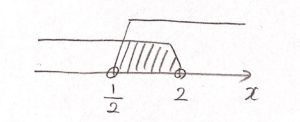
(注3)[1]と[2]の範囲を合体する(つなげる)
※ [1]または[2] と考える

【参考】共通範囲のカンタンな取り方
例: $−4 ≦ x ≦ 6$ かつ $x > 3$ かつ $x < −2$
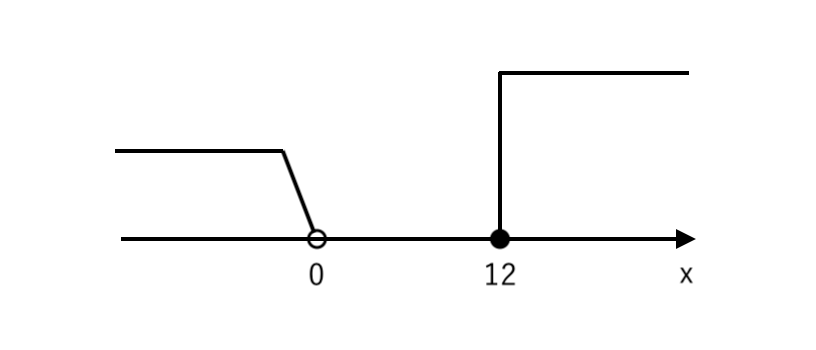
① 数直線を描く

② 境界値をとる(左から小さい順に並べるだけ)
※ 間隔はテキトーでOK
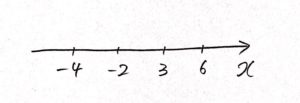
③ <, >なら白丸(○)、≦, ≧なら黒丸(●)を描く
※ 大きくハッキリと
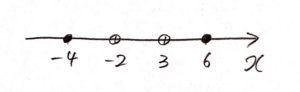
④ <, >ならナナメに、≦, ≧なら真上に線を描きはじめる(高さを少しずつズラす)
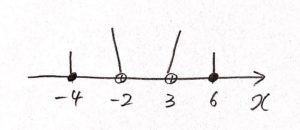
⑤ 範囲の方向に横線を引く
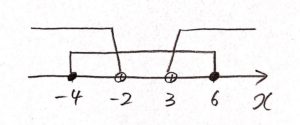
⑥ 範囲が重なる部分に斜線を描く

【別解】簡便法
参考として、この【例題4】「$|x − 2| < 3x$ を解け。」も 簡便法 を使って解いてみます。
- 【別解】を見る
-
【別解】
$\color{red}{0≦} |x − 2| < 3x$ より
$ $ $ \color{red}{0≦} 3x $
∴ $ x ≧ 0 $
このとき
$ $ $ − 3x < x − 2 < 3x $ ・・・(注)
∴ $ − 3x < x − 2 \ \color{red}{かつ} \ x − 2 < 3x $
∴ $ \displaystyle {x>{1\over2}\ \color{red}{かつ} \ x>−1} $
∴ $ \displaystyle {x>{1\over2}} $
$ x ≧ 0 $ より $ \displaystyle {x>{1\over2}} $
(注)この不等式は、左の2辺、右の2辺に分けて解きますが、その2式は「$\color{red}{かつ}$」の条件であることに注意!
【パターン5】絶対値の等式 |x| + |x − 2| = 4 の解き方
いよいよラストです。
「絶対値つきの変数が2つ以上ある」パターンです。
【例題5】 $|x| + |x − 2| = 4$ を解け。
今回も絶対値の中身が「0以上」か「マイナス」かで場合分けをします。
絶対値の中身が「$x$」と「$x − 2$」の2種類あるので、本来なら以下の4つの場合分けがありますが、
| $x$ | $x − 2$ | |
|---|---|---|
| ① | + | + |
| ② | + | − |
| ③ | − | + |
| ④ | − | − |
$x > x − 2$ より、
③「$x$:マイナス、$x − 2$:0以上」の場合はありえません。
なので、①、②、④の3つの場合分けで済みます。
「$x ≧ 2$」のとき
「$0 ≦ x < 2$」のとき
「$x < 0$」のとき
【応用問題】絶対値のついた等式・不等式
ちょっと難しめの問題を解きたい人は、次の2問にチャレンジしてみましょう!
ここまでの内容が理解できていれば、なんとか解けるはずです。
【問題1】方程式 $|2x + 2| − |x − 3| = 2x$ を解け。
この問題を見て「あれ?$2x + 2$ と $x−3$ はどっちが大きいの?」と思ったキミ、いいところに気がつきました。
$2x + 2$ と $x−3$ はこの形のままでは比べられませんね。
ですが、$ |2x + 2| = |2(x +1)| $ と変形していくと・・・
- 【解答・解説】を見る
-
【解答】
$|2x + 2| − |x − 3| = 2x$ より
$|2(x + 1)| − |x − 3| = 2x$
∴ $ 2| x + 1 | − | x − 3 | = 2x $ ・・・(注1)
$ x + 1 > x − 3 $ より、以下の3つに場合分けできる。 ・・・(注2)
$ $[1] 「$ x + 1 \color{red}{≧ 0} $ かつ $ x − 3 \color{red}{≧ 0} $」すなわち「$ x≧3 $」のとき
$ $ $ 2( x + 1 ) − ( x − 3 ) = 2x $
$ $ ∴ $ x = 5 $ ($ x≧3 $ を満たす)
[2] 「$ x + 1 \color{red}{≧ 0} $ かつ $ x − 3 \color{blue}{< 0} $」すなわち「$ −1≦x<3 $」のとき$ $ $ 2( x + 1 ) + ( x − 3 ) = 2x $
$ $ ∴ $ x = 1 $ ($ −1≦x<3 $ を満たす)
[3] 「$ x + 1 \color{blue}{< 0} $ かつ $ x − 3 \color{blue}{< 0} $」すなわち「$ x<−1 $」のとき$ $ $ −2( x + 1 ) + ( x − 3 ) = 2x $
$ $ ∴ $ \displaystyle { x = −{ 3 \over 5 } } $ ($ x<−1 $ を満たす)
[1]〜[3]より、$ \displaystyle { x = −{ 3 \over 5 }, \enspace 1, \enspace 5 } $(注1)$ |2x + 2| = |2(x +1)| = 2| x + 1 | $ と変形できます。
ちなみに、例えば $|−x + 3 | = |−(x − 3) | = | x−3 | $ などの変形もOK。
(注2)$ x + 1 > x − 3 $ なので、「$x + 1$:マイナス、$x − 3$:0以上」の場合はあり得ないので、考えなくて大丈夫。
【問題2】不等式 $\displaystyle { |x − 5| ≦{2 \over 3}|x| + 1 }$ を解け。
「絶対値つきの変数が2つ以上ある 不等式」のパターンです。やり方は今までと同じです。
- 【解答・解説】を見る
-
【解答】
$ x − 5 < x $ より、以下の3つに場合分けできる。
$ $[1] 「$ x − 5 \color{red}{≧ 0} $ かつ $ x \color{red}{≧ 0} $」
すなわち「$ x≧5 $」のとき$ $ $\displaystyle { x − 5 ≦{2 \over 3} x + 1 }$
$ $ ∴ $ x ≦ 18 $
$ $ $ x≧5 $ より $ 5≦x≦18 $
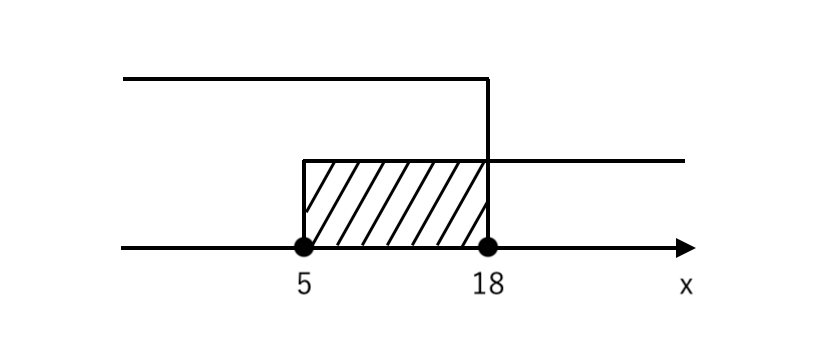
[2] 「$ x − 5 \color{blue}{< 0} $ かつ $ x \color{red}{≧ 0} $」
すなわち「$ 0 ≦x<5 $」のとき$ $ $\displaystyle { −( x − 5 ) ≦{2 \over 3} x + 1 }$
$ $ ∴ $\displaystyle { x ≧ {12 \over 5} } $
$ $ $ 0 ≦x<5 $ より $ \displaystyle { {12 \over 5} ≦ x < 5 } $
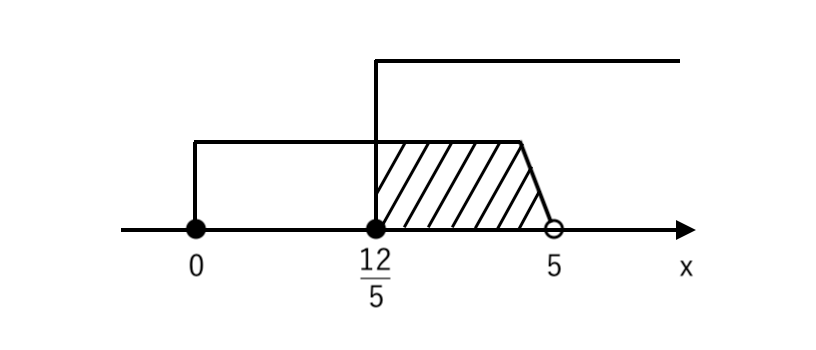
[3] 「$ x − 5 \color{blue}{< 0} $ かつ $ x \color{blue}{< 0} $」
すなわち「$ x<0 $」のとき$ $ $\displaystyle { −( x − 5 ) ≦− {2 \over 3} x + 1 }$
$ $ ∴ $ x ≧ 12 $
$ $ $ x<0 $ より 解なし(不適)
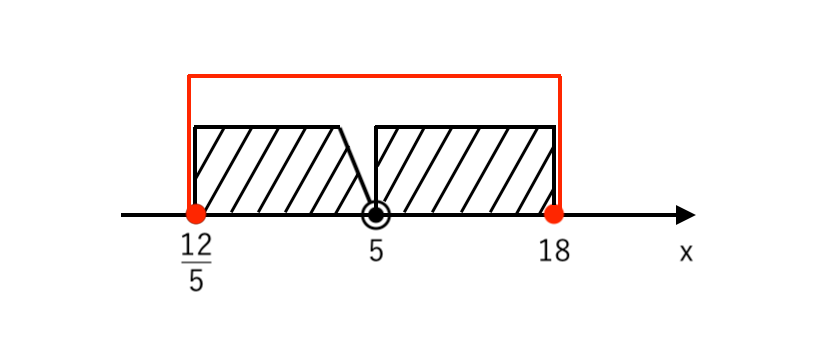
[1]〜[3]より、$ \displaystyle { {12 \over 5} ≦ x ≦18 } $ ・・・(注)(注)[1]〜[3]の範囲を合体する(つなげる)