2次関数の「最大値と最小値を求める問題」がよくわからない・・・
グラフを使ってどうやって求めればいいの?
2次関数の最大値と最小値の簡単な求め方を教えてほしい!
こういった要望に応えます。
2次関数の最大値・最小値を求める問題 で、バカ真面目に $xy$平面にグラフをかいて解いていませんか?
もしキミが頂点や $y$切片などもしっかり考慮したグラフで解いているとしたら、ハッキリ言って「時間の無駄」です。
そんなことをしなくても 2次関数の最大値・最小値 は簡単に求められるし、◎ がもらえるような答案を素早く作ることができます。
今回は「2次関数の最大値・最小値を 手抜きグラフで速答 する方法」をお教えします。
【2次関数】最大値と最小値の求め方【手抜き速答法】

2次関数の最大値・最小値を 手抜きグラフで速答 する方法 は以下の通り。
- 放物線を(薄めに)かく
- 横軸($x$ 軸)をかく
- 「$x$の範囲の端っこ」「放物線の軸」の値 をとる
- 放物線にプロットする
- 範囲の部分を濃く塗る
- 高さが 最大・最小 の点を読み取る
ポイント は、
- $y$軸をかかない
- 真面目に(厳密に)考えない
という2点です。
「〜のグラフをかけ」という問題でなければ、手抜きグラフでもちゃんと ◎(満点)がもらえます。
例題を通して、具体的な手順を解説していきます。
【2次関数】最大値と最小値の求め方(下に凸の場合)

はじめに、2次関数の最大値・最小値の求め方(下に凸の場合) を見ていきましょう!
まずは 平方完成 して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ $ $ y = ( x −1 )^2 −2 $
∴ $ \begin{cases}
頂点 \enspace (1, −2) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。
ここから 簡単な手抜きグラフ をかいて最大値・最小値を求めていきます。
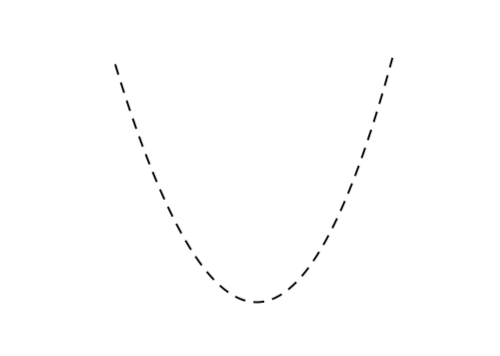
① 下に凸 の放物線を(薄めに)かく
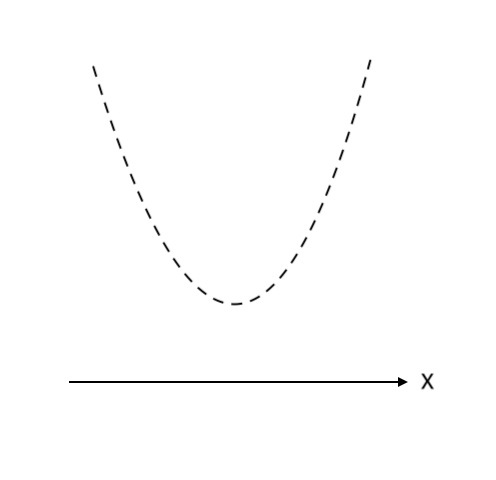
② その下に横軸($x$ 軸)をかく
③ 「$x$の範囲の端っこ」「放物線の軸」の値 をとる
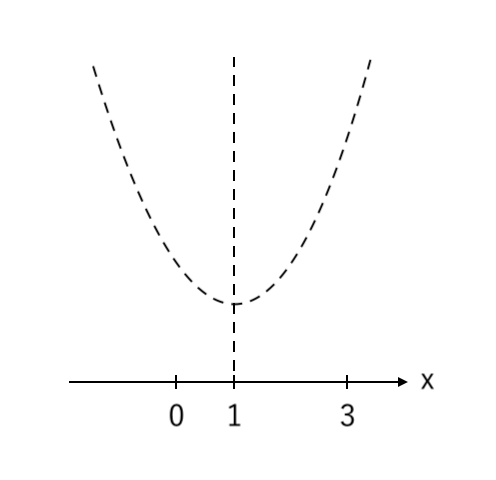
※ 注意点:軸からの 左右のバランス を考えること!
$ $ この問題なら、左〜軸(0〜1)はせまく、軸〜右(1〜3)は広くなるように書く
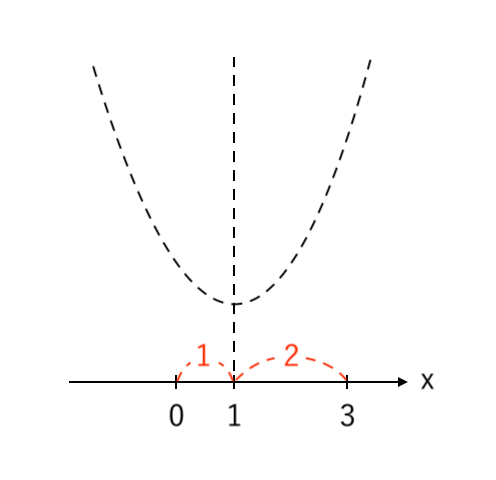
④ 放物線にプロットする
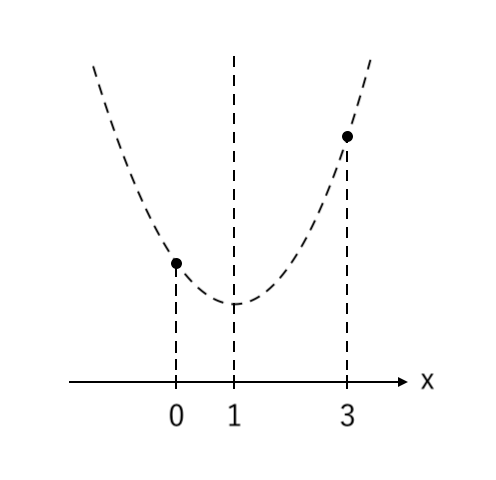
⑤ 範囲の部分を濃く塗る
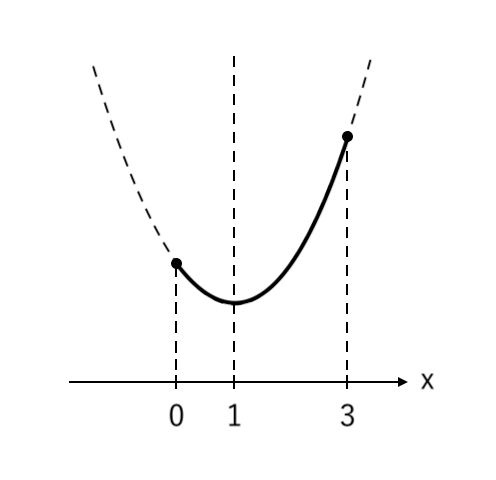
⑥ 高さが 最大・最小 の点を読み取る
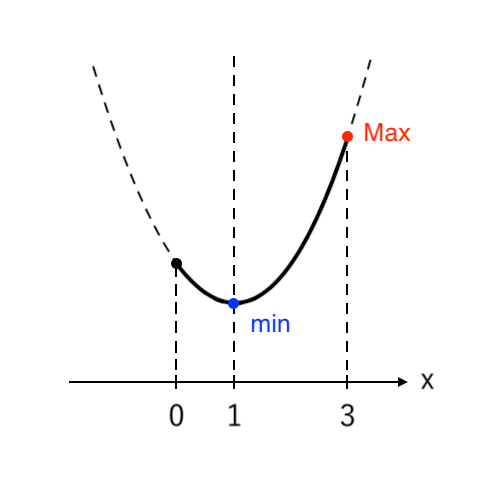
$ 0≦x≦3 $ より、$y$ は
$ \begin{cases}
x = 3 \enspace で \color{red}{最大値 \enspace 2} \\
\\
x = 1 \enspace で \color{blue}{最小値 \enspace−2} \\
\end{cases}$
をとる。
こんな感じです。
どうでしたか? 真面目にグラフをかくときと比べて、はやく解けましたよね?
この問題が答えてほしいのは「最大値と最小値」だけなので、必ずしも正確なグラフを書く必要はありません。
頂点や $y$切片が $xy$平面上のどの位置にあるのか?なんて、ハッキリ言って「どうでもいい」のです。
正しいプロセスで「最大値と最小値」さえ求められれば ◎ がもらえるわけですね。
【2次関数】最大値と最小値の求め方(上に凸の場合)

次に、2次関数の最大値・最小値の求め方(上に凸の場合) を見ていきましょう!
やはり、まず平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ $ $ y = −( x −2 )^2 + 5 $
∴ $ \begin{cases}
頂点 \enspace (2, 5) \\
\\
軸:x = 2 \\
\\
上に凸 \\
\end{cases}$ の放物線。
ここから 簡単な手抜きグラフ をかいて最大値・最小値を求めていきます。
さっきの「下に凸」の場合と、上下逆さまになるだけですね。
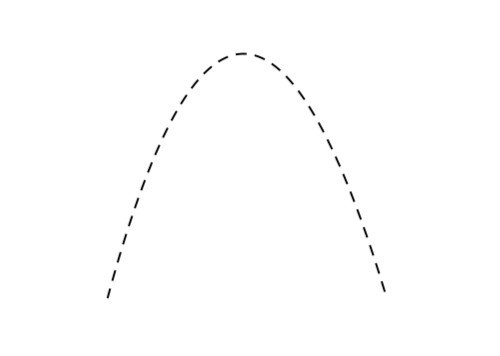
① 上に凸 の放物線を(薄めに)かく
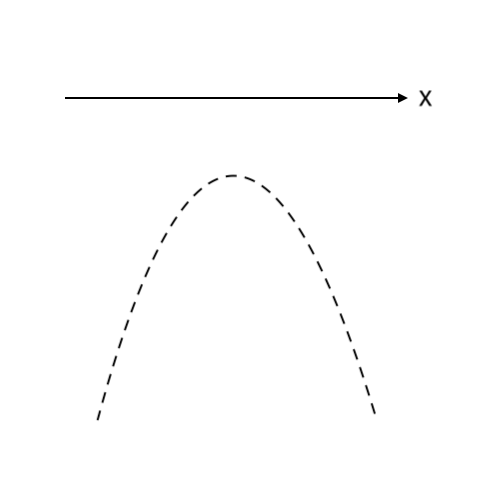
② その上に横軸($x$ 軸)をかく
③ 「$x$の範囲の端っこ」「放物線の軸」の値 をとる
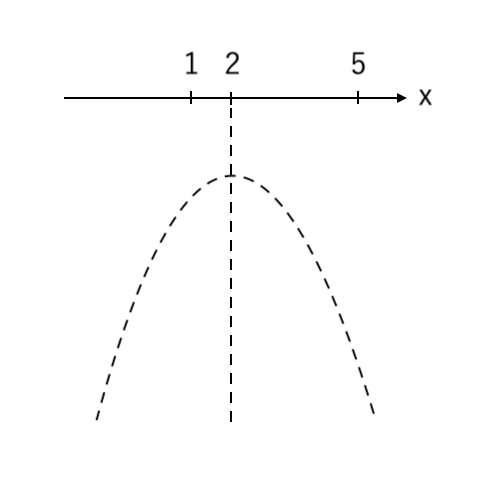
※ 注意点:軸からの 左右のバランス を考えること!
$ $ この問題なら、左〜軸(1〜2)はせまく、軸〜右(2〜5)は広くなるように書く
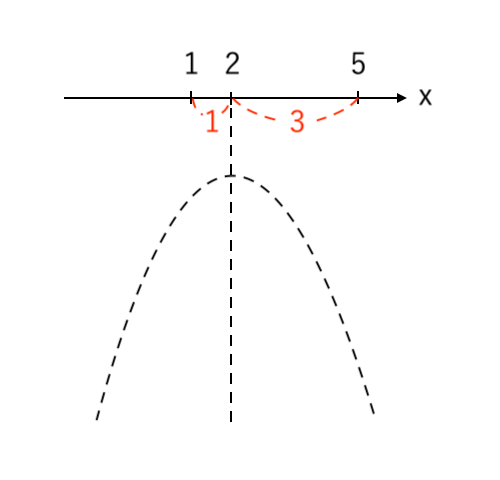
④ 放物線にプロットする
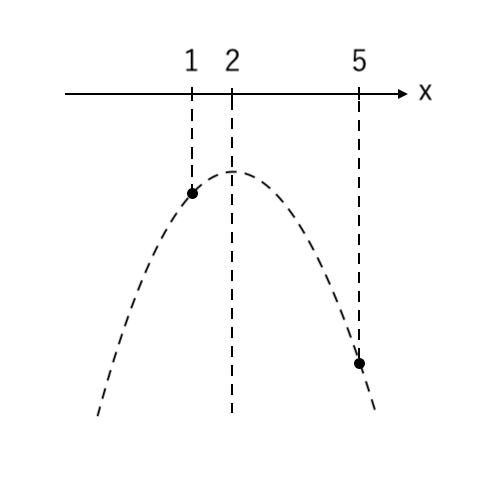
⑤ 範囲の部分を濃く塗る
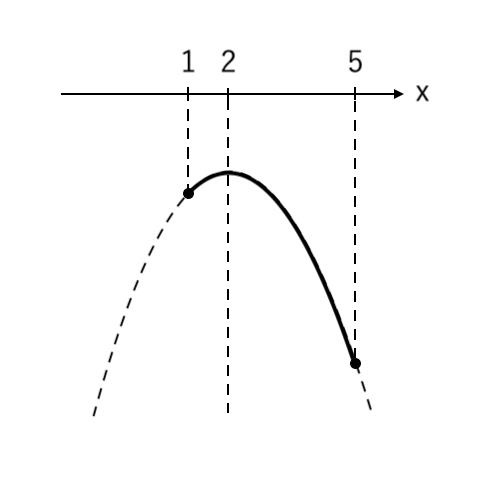
⑥ 高さが 最大・最小 の点を読み取る
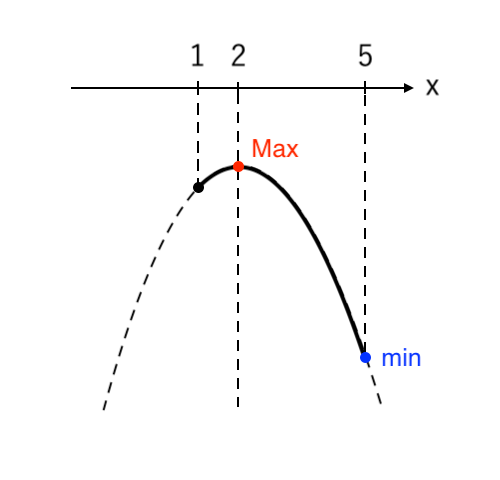
$ 1≦x≦5 $ より、$y$ は
$ \begin{cases}
x = 2 \enspace で \color{red}{最大値 \enspace 5} \\
\\
x = 5 \enspace で \color{blue}{最小値 \enspace−4} \\
\end{cases}$
をとる。
こんな感じで、最大値と最小値が求められました。
2次関数の最大値と最小値を求めよう!【練習問題】
上で説明したやり方で、2次関数の最大値と最小値を求める問題 を解いてみましょう!
【問題】次の2次関数の最大値と最小値を求めよ。
(1) $ y = 2x^2 −8 x + 5 $ $( 0≦x≦3 )$
(2) $ y = −x^2 −2 x + 2 $ $(−3≦x≦−2)$
(3) $ y = x^2 + 4 x − 1 $ $( 0≦x≦2 )$
(4) $ \displaystyle { y = −{1 \over 2}x^2 + 2 x + {3 \over 2} } $ $( −1 ≦x≦3 )$
(5) $ y = −x^2 + 6 x −7 $ $(2<x<5)$
- 【解答】を見る
-
【解答】
(1) $ y = 2x^2 −8 x + 5 $
$ $ $ = 2(x^2 −4 x) + 5 $
$ $ $ = 2(x −2)^2 −4 \cdot 2 + 5 $
$ $ $ = 2(x −2)^2 −3 $
∴ $ \begin{cases}
頂点 \displaystyle { \left( 2 , −3 \right) } \\
\\
軸: \displaystyle { x = 2 } \\
\\
下に凸
\end{cases}$ の放物線。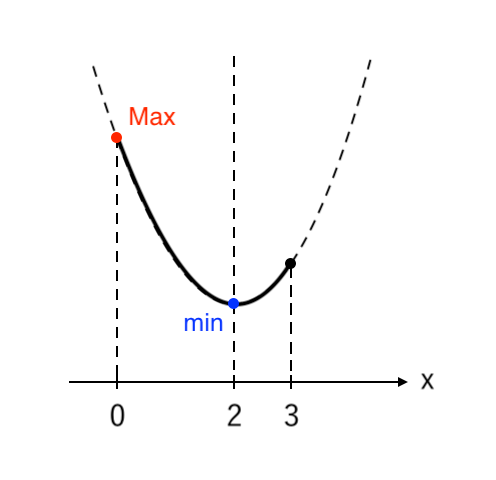
$ $ $ 0≦x≦3 $ より、$y$ は
$ $ $ \begin{cases}
x = 0 \enspace で \color{red}{最大値 \enspace 5} \\
\\
x = 2 \enspace で \color{blue}{最小値 \enspace−3} \\
\end{cases}$$ $ をとる。
(2) $ y = −x^2 −2 x + 2 $
$ $ $ = −(x^2 +2 x) + 2 $
$ $ $ = −(x +1)^2 −1 \cdot (−1) + 2 $
$ $ $ = −(x +1)^2 + 3 $
∴ $ \begin{cases}
頂点 \displaystyle { \left( −1 , 3 \right) } \\
\\
軸: \displaystyle { x = −1 } \\
\\
上に凸
\end{cases}$ の放物線。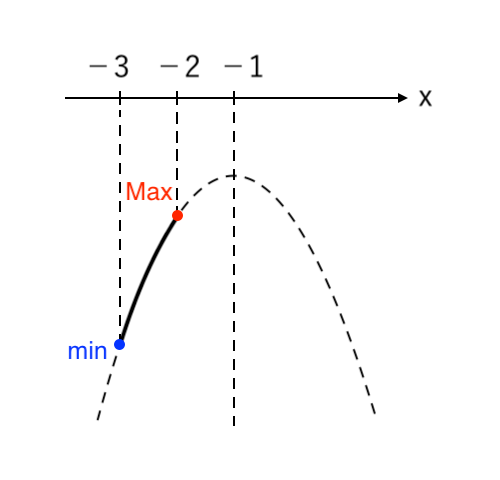
$ $ $ −3≦x≦−2 $ より、$y$ は
$ $ $ \begin{cases}
x = −2 \enspace で \color{red}{最大値 \enspace 2} \\
\\
x = −3 \enspace で \color{blue}{最小値 \enspace−1} \\
\end{cases}$$ $ をとる。
(3) $ y = x^2 + 4 x − 1 $
$ $ $ = (x + 2)^2 −4 − 1 $
$ $ $ = (x + 2)^2 −5 $
∴ $ \begin{cases}
頂点 \displaystyle { \left( −2 , −5 \right) } \\
\\
軸: \displaystyle { x = −2 } \\
\\
下に凸
\end{cases}$ の放物線。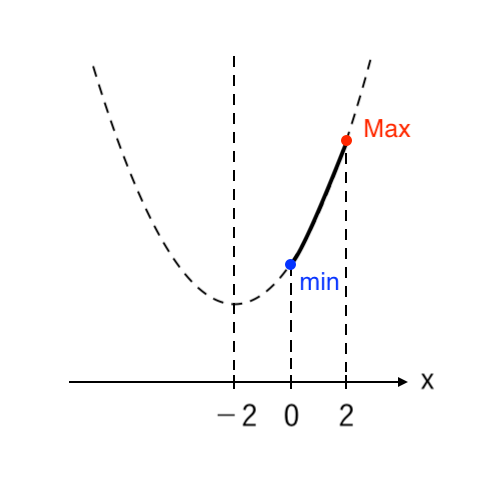
$ $ $ 0≦x≦2 $ より、$y$ は
$ $ $ \begin{cases}
x = 2 \enspace で \color{red}{最大値 \enspace 11} \\
\\
x = 0 \enspace で \color{blue}{最小値 \enspace−1} \\
\end{cases}$$ $ をとる。
(4) $ \displaystyle { y = −{1 \over 2}x^2 + 2 x + {3 \over 2} } $
$ $ $\displaystyle { = −{1 \over 2}(x^2 −4 x) + {3 \over 2} } $
$ $ $\displaystyle { = −{1 \over 2}(x −2)^2 −4 \cdot \left( −{1 \over 2} \right) + {3 \over 2} } $
$ $ $\displaystyle { = −{1 \over 2}(x −2)^2 + {7 \over 2} } $
∴ $ \begin{cases}
頂点 \displaystyle { \left( 2 , {7 \over 2} \right) } \\
\\
軸: \displaystyle { x = 2 } \\
\\
上に凸
\end{cases}$ の放物線。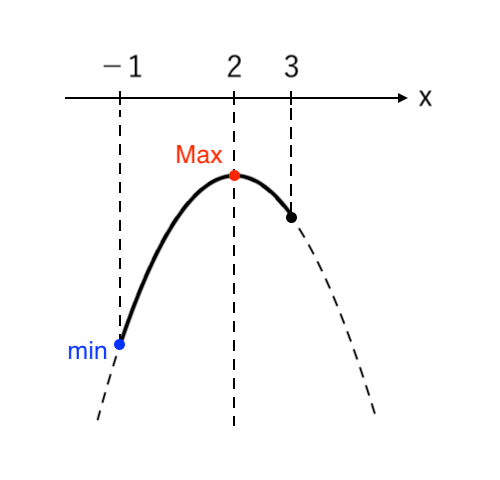
$ $ $ −1 ≦x≦3 $ より、$y$ は
$ $ $ \begin{cases}
x = 2 \enspace で \color{red}{最大値 \enspace \displaystyle {7 \over 2} } \\
\\
x = −1 \enspace で \color{blue}{最小値 \enspace −1 } \\
\end{cases}$$ $ をとる。
(5) $ y = −x^2 + 6 x −7 $ $(2<x<5)$
$ $ $ = −(x^2 −6 x) −7 $
$ $ $ = −(x −3)^2 −9 \cdot (−1) −7 $
$ $ $ = −(x −3)^2 + 2 $
∴ $ \begin{cases}
頂点 \displaystyle { \left( 3 , 2 \right) } \\
\\
軸: \displaystyle { x = 3 } \\
\\
上に凸
\end{cases}$ の放物線。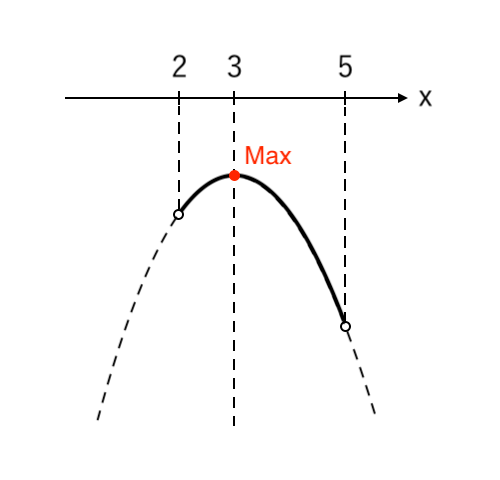
$ $ $ 2<x<5 $ より、$y$ は
$ $ $ \begin{cases}
x = 3 \enspace で \color{red}{最大値 \enspace 2} \\
\\
\color{blue}{最小値 \enspace なし } \\
\end{cases}$ ・・・(注)(注)$ 2<x<5 $ なので、端っこの点はグラフ上に○で書いています(端っこを含まない)。ゆえに、最小値をとるような $x$の値も存在しません。
【まとめ】2次関数の最大値・最小値の求め方
最後に「2次関数の最大値・最小値を 手抜きグラフで速答 する方法」をまとめておきます。
- 放物線を(薄めに)かく
- 横軸($x$ 軸)をかく
- 「$x$の範囲の端っこ」「放物線の軸」の値 をとる
- 放物線にプロットする
- 範囲の部分を濃く塗る
- 高さが 最大・最小 の点を読み取る
- $y$軸をかかない
- 真面目に(厳密に)考えない
たくさん問題を解いて、2次関数の最大値・最小値の求め方に慣れていきましょう!
質問・要望があれば気軽にコメントください👍