「相加・相乗平均の関係」で最大値を求める問題がよく分からない
テスト・入試によく出る問題をわかりやすく解説してほしい!
こういった要望に応えます。
このページでは「相加・相乗平均の関係」で 最大値 を求める問題をわかりやすく&丁寧に解説しました。
学校のテストや大学入試でよく出るパターンの問題を厳選したので、最後までしっかりと読んでおきましょう!
相加・相乗平均の関係とは?
はじめに「相加・相乗平均の関係」のおさらいです。
$ a>0, \ b>0 $ のとき
$ $ $ \displaystyle{ a + b ≧ 2 \sqrt{ ab } } $
等号成立条件 は $ a=b $ ← 忘れずに!
(等号成立は $ a=b $ のとき)
「相加・相乗平均の関係」が使える条件
- 正の数
- 2数の足し算
- 逆数の(ような)形
この3つの条件がすべて揃って、はじめて「相加・相乗平均の関係」が使えます。
「相加・相乗平均の関係」で最小値がなぜ求められるの? そもそも「相加平均・相乗平均」ってどういう意味なの? 図を使ってわかりやすく証明してほしい! こういった要望に答えます。 相加・相乗平均の関係とは? 「相加・相乗平均の[…]
【相加・相乗平均の関係】最大値を求める問題
さっそく「相加・相乗平均の関係」で 最大値 を求める問題 を見てみましょう。
【例題1】$x>0$ のとき、$ \displaystyle{ { x \over x^2 + 3x + 5 } } $ の最大値と、そのときの $x$ の値を求めよ。
こんな問題に「相加・相乗平均の関係」が使えるの?という見た目ですが、分母・分子を $x$ で割ると・・・
【解答】
$ \displaystyle{ { x \over x^2 + 3x + 5 } = { 1 \over \displaystyle{ x + 3 + {5 \over x} } } } $
$ $ $ = \displaystyle{ 1 \over \displaystyle{ x + {5 \over x} + 3 } } $
ここまで変形すると、$x\color{red}{>0}$(条件①)、$ \displaystyle{ x \color{red}{+} {5 \over x} } $(条件①、③)より、「相加・相乗平均の関係」が使えそうですね。
$x>0$ より $ \displaystyle{ {5 \over x}>0 } $ なので
相加・相乗平均の関係により
$ $ $ \displaystyle{ x + {5 \over x} + 3 ≧ 2 \sqrt{ \require{cancel} \bcancel{x} \cdot { 5 \over \bcancel{x} } } + 3 = 2 \sqrt{5} + 3 } $
両辺の逆数をとると
$ $ $ \displaystyle{ { 1 \over \displaystyle{ x + {5 \over x} + 3 } } \color{red}{≦} { 1 \over 2 \sqrt{5} + 3 } } $
ここの計算については、例えば
$ $ $ \displaystyle{ 3 > 2 } $
の逆数をとると
$ $ $ \displaystyle{ {1 \over 3} \color{red}{<} {1 \over 2} } $
のように大小が逆になります。
これで最大値が分かったので、忘れずに 等号成立条件 の確認をしましょう。
等号成立条件は
$ $ $ \displaystyle{ x = {5 \over x} } $
両辺に $x$ をかけると
$ $ $ x^2 = 5 $
$x>0$ より $ x= \sqrt{5} $
最後に答えをまとめます。
したがって
$ $ $ x= \sqrt{5} $ で
$ $ 最大値 $\displaystyle{ { 1 \over 2 \sqrt{5} + 3 } = { 2 \sqrt{5} − 3 \over 11 } } $
【例題2】$x,\ y$ が $x>0, \ y>0,$ $ 3x+5y=20$ を満たしながら動くとき、$\sqrt{xy}$ の最大値と、そのときの $x, \ y$ の値を求めよ。
$x\color{red}{>0}, \ y\color{red}{>0}$(条件①)、$3x \color{red}{+}5y=20$(条件②)に着目すると「相加・相乗平均の関係」が使えそうだ!と判断できます。
【解答】
$x>0, \ y>0$ より $3x>0, \ 5y>0$ なので
相加・相乗平均の関係により
$ $ $ 3x+5y ≧ 2 \sqrt{ 3x \cdot 5y }$
∴ $ 3x+5y ≧ 2 \sqrt{ 15xy }$
$3x+5y=20$ より
$ $ $ 20 ≧ 2 \sqrt{ 15xy }$
∴ $ \displaystyle{ { 10 \over \sqrt{15} } ≧ \sqrt{ xy } } $
∴ $ \displaystyle{ \sqrt{ xy } ≦ { 10 \over \sqrt{15} } = { 2 \sqrt{15} \over 3 } } $
これで最大値が求められました。
次に等号成立条件の確認です。
等号成立条件は
$ $ $ 3x=5y $
$3x+5y=20$ に代入して
$ $ $3x+3x=20$
∴ $ \displaystyle{ x = {10 \over 3} } $
∴ $ \displaystyle{ y = {3 \over 5}x = 2 } $
最後にまとめておきます。
したがって、$\sqrt{ xy }$ は
$ $ $ \displaystyle{ x = {10 \over 3}, \ y = 2 } $ で 最大値 $ \displaystyle{ { 2 \sqrt{15} \over 3 } } $
スッキリとした解答になりましたね。
別解
「相加・相乗平均の関係」を使わない別解もあります。
$y$ を消去して、$\sqrt{xy}$ を「$x$ だけの式」に変形する解き方です。
【別解】
$3x+5y=20$ より
$ $ $ \displaystyle{ y=4−{3 \over 5}x } $ ・・・①
$y>0$ より
$ $ $\displaystyle{4−{3 \over 5}x>0}$
∴ $ \displaystyle{ x < {20 \over 3} } $
$x>0$ より
$ $ $ \displaystyle{ 0< x < {20 \over 3} } $ ・・・②
$x$ の範囲が求められました。
次に $\sqrt{xy}$ を「$x$ だけの式」にします。
① を $\sqrt{xy}$ に代入して
$ \displaystyle{ \sqrt{xy} = \sqrt{x \left( 4−{3 \over 5}x \right) } } $
$ $ $ \displaystyle{ = \sqrt{ 4x −{3 \over 5}x^2 } } $
$ $ $ \displaystyle{ = \sqrt{−{3 \over 5}x^2 + 4x } } $
$\sqrt{ \enspace }$ の中をよく見ると、$x$ の2次関数になっていますね。
ここからは、「2次関数の最大・最小を求める問題」と同じやり方です。
2次関数の「最大値と最小値を求める問題」がよくわからない・・・ グラフを使ってどうやって求めればいいの? 2次関数の最大値と最小値の簡単な求め方を教えてほしい! こういった要望に応えます。 2次関数の[…]
まずは平方完成します。
$ $ $ \displaystyle{ = \sqrt{−{3 \over 5} \left( x^2 −{20 \over 3}x \right) } } $
$ $ $ \displaystyle{ = \sqrt{−{3 \over 5} \left( x −{10 \over 3} \right)^2−\left( {10 \over 3} \right)^2 \cdot \left( −{3 \over 5} \right) } } $
$ $ $ \displaystyle{ = \sqrt{−{3 \over 5} \left( x −{10 \over 3} \right)^2 + {20 \over 3} } } $
この平方完成のやり方がよく分からない!という人は次の記事でおさらいしておきましょう。
二次関数の「平方完成」の計算に手間取ったり、しかもミスをよくしてしまう 平方完成を素早く、確実に、簡単に計算する方法を知りたい! そもそもなぜ平方完成するの? 平方完成はいつ使うの? 今回の記事では、こういった悩み・疑問[…]
さて、平方完成ができたので、簡単なグラフをかいて 最大値 を読み取りましょう。
$ \displaystyle{ f(x) = −{3 \over 5} \left( x −{10 \over 3} \right)^2 + {20 \over 3} } $ とすると
$ y=f(x) $ は
$ \begin{cases}
頂点 \enspace \displaystyle{ \left( {10 \over 3} , {20 \over 3} \right) } \\
\\
軸:\displaystyle{ x = {10 \over 3} } \\
\\
上に凸 \\
\end{cases}$
の放物線。
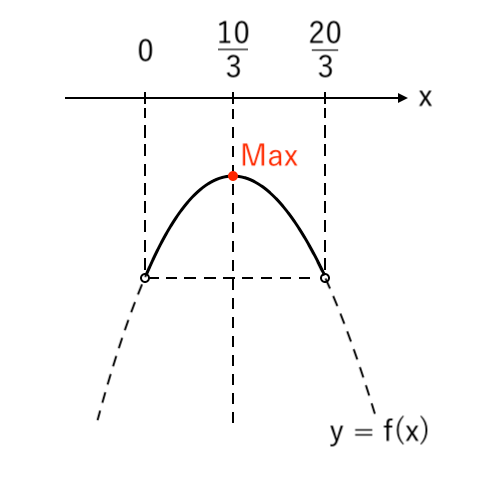
② の範囲において、$ f(x) $ は
$ $ $ \displaystyle{ x = {10 \over 3} } $ で 最大値 $ \displaystyle{ {20 \over 3} } $
このとき、① より $ \displaystyle{ y=2 } $
$ f(x) $ が最大値をとるとき、$ \sqrt{f(x)} = \sqrt{xy} $ も最大値をとる。 ・・・(注)
したがって、$ \sqrt{xy} $ は
$ $ $ \displaystyle{ x = {10 \over 3} , \ y=2 } $ で 最大値 $ \displaystyle{ \sqrt{20 \over 3} = { 2 \sqrt{15} \over 3 } } $
(注)ここについては、数学Ⅲ「無理関数」を学ぶとスッキリ理解できます。
関数 $ y= \sqrt{x} \enspace (x>0) $ のグラフは
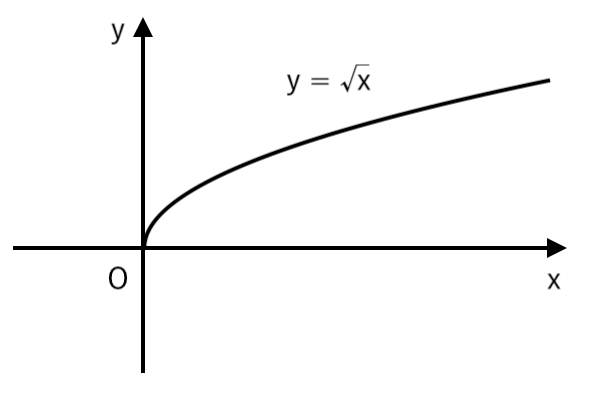
こんな感じに「単調増加」($x$ が増えると $y$ も増える)します。
なので、$ \sqrt{\enspace}$ の中の数($\color{red}{x}$)が最大のとき、$\sqrt{\color{red}{x}}$ も最大というわけです。
以上です。お疲れ様でした!
【相加・相乗平均の関係】最小値を求める問題
なお、「相加・相乗平均の関係」で 最小値 を求める問題 はこちら。
「相加・相乗平均の関係」の使い方や条件、タイミングがよく分からない 「相加・相乗平均の関係」っていつ使ったらいいの? 証明問題や最小値を求める問題をわかりやすく解説してほしい! こういったお悩みを解決します。 […]
質問・要望があれば気軽にコメントください👍