「相加・相乗平均の関係」で最小値がなぜ求められるの?
そもそも「相加平均・相乗平均」ってどういう意味なの?
図を使ってわかりやすく証明してほしい!
こういった要望に答えます。
相加・相乗平均の関係とは?
「相加・相乗平均の関係」は次の通り。
$ a>0, \ b>0 $ のとき
$ $ $ \displaystyle{ {a + b \over 2} ≧ \sqrt{ ab } } $
$ $ $ \Leftrightarrow \displaystyle{ a + b ≧ 2 \sqrt{ ab } } $
等号成立条件は $ a=b $
(等号成立は $ a=b $ のとき)
もうちょっとシンプルに言えば
2つの正の数について
$ $ $ \displaystyle{ {和 \over 2} ≧ \sqrt{ 積 } } $
$ \Leftrightarrow \displaystyle{ 和 ≧ 2 \sqrt{ 積 } } $
等号成立は、2つの数が等しいとき
このように理解してもOK!
相加平均(そうかへいきん)
左辺の $ \displaystyle{ {a + b \over 2} \ \left( {和 \over 2} \right) } $ は「相加平均」と言います。
足して2で割るという、いわゆる「平均」のことですね。
相乗平均(そうじょうへいきん)
右辺の $ \sqrt{ ab } \ \left( \sqrt{ 積 } \right) $ は「相乗平均(幾何平均)」と言います。
あまり聞き慣れないワードですが、人口増加率や経済成長率などの「変化率の平均」を計算するときに使います。
【相加・相乗平均の関係】最小値がなぜ求められるの?
【例】$ a>0, \ b>0 , ab = 3 $ のとき、$ a+b $ の最小値を求めよ。
例えば、このような問題で「相加・相乗平均の関係 で 最小値 がなぜ求められるのか?」というと
という形になってくれるからです。
この「定数」こそが 最小値 になる(かもしれない)というわけです。
「かもしれない」と言った理由は
最小値 $2 \sqrt{3} $ をとるような $a,\, b$ の値が本当に存在するか、まだ分からないからです。
なので、必ず
と書くのを忘れずに!
「相加・相乗平均の関係」の意味は?図で証明
「そもそも 相加・相乗平均の関係 ってどういう意味?」という本質を理解するために、図形的に証明してみます。
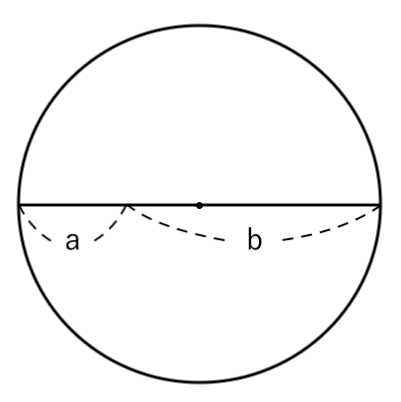
上図のような、直径 $a+b$ の円を用意します($ a>0, \ b>0 $)。
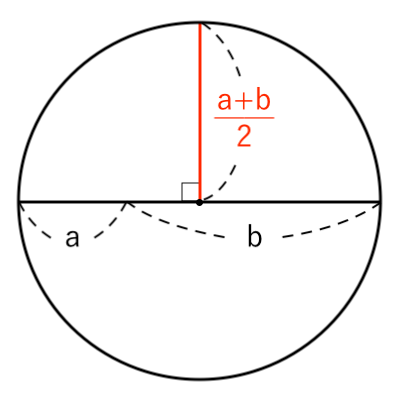
赤色 の長さは、円の半径なので
$ $ $ \displaystyle{ {a + b \over 2} } $(相加平均)
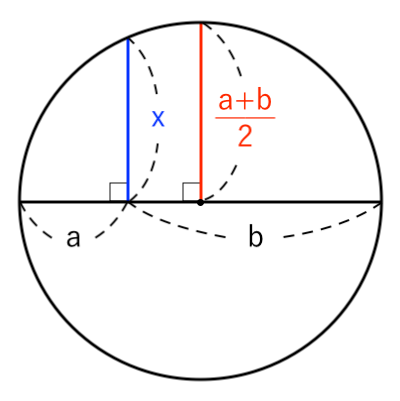
青色 の長さを $x$ とおいて
$x$ を、$a, \ b $ を使って表します。
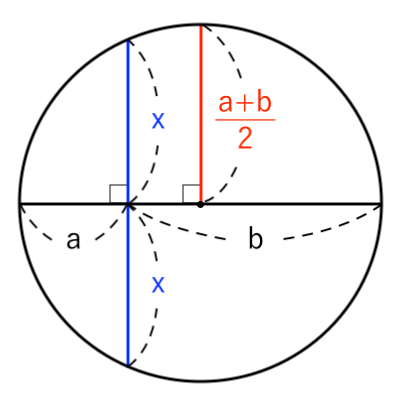
方べきの定理より
$ $ $ x \cdot x = a \cdot b $
∴ $ x^2 = ab $
$a>0, \ b>0$ より
$ $ $ x = \sqrt{ ab } $(相乗平均)
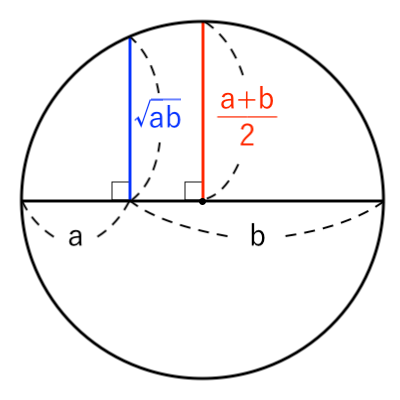
図より
$ $ $ \displaystyle{ \color{red}{a + b \over 2} ≧ \color{blue}{ \sqrt{ ab } } } $
$ $ $ \color{red}{(相加平均)}≧\color{blue}{ (相乗平均)} $
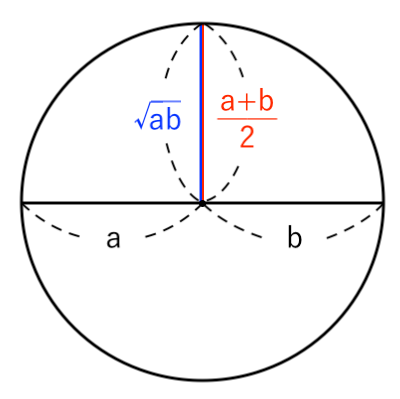
等号成立条件は、上図のようなときなので
$ $ $ a=b$(半径) [終]
以上をまとめると
$ a>0, \ b>0 $ のとき
$ $ $ \displaystyle{ {a + b \over 2} ≧ \sqrt{ ab } } $
等号成立条件は $ a=b $
こんな感じで図形的に証明できました。
「相加・相乗平均の関係」の意味は?グラフで証明
もう一個、証明として「相加・相乗平均の関係 の 意味」をグラフで説明してみます。
$2$ 次関数 $y=x^2$ のグラフを利用します。

関数 $y=x^2$ 上の $3$ 点 $A ( \sqrt{a}, \ a) ,$ $B ( \sqrt{b}, \ b) , $ $\displaystyle{ P \left( {\sqrt{a}+\sqrt{b} \over 2} , \ \left( {\sqrt{a}+\sqrt{b} \over 2} \right)^2 \right) } $ と
$A, \ B $ の中点 $\displaystyle{ Q \left( {\sqrt{a}+\sqrt{b} \over 2} , \ {a+b \over 2} \right) } $ を定めます。
$y=x^2$ は下に凸の増加関数なので、$P, \ Q$ の高さ($y$ 座標)を比べると
$ $ $(Q の y 座標) ≧ (P の y 座標) $
∴ $\displaystyle{ {a+b \over 2} ≧ \left( {\sqrt{a}+\sqrt{b} \over 2} \right)^2 } $
∴ $\displaystyle{ {a+b \over 2} ≧ { a + b + 2 \sqrt{ab} \over 4} } $
∴ $\displaystyle{ {a+b \over 4} ≧ { \sqrt{ab} \over 2} } $
∴ $ \displaystyle{ \color{red}{a + b \over 2} ≧ \color{blue}{ \sqrt{ ab } } } $
$ $ $ \color{red}{(相加平均)}≧\color{blue}{ (相乗平均)} $
等号成立条件は、「$P$ と $Q$ が一致する」
つまり、「$A$ と $B$ が一致する」ことなので
$ $ $ a=b$ [終]
このようにグラフを使っても証明できます。
参考:「相加・相乗平均の関係」の証明
参考までに、図・グラフを使わない一般的なやり方でも証明しておきます。
$ a>0, \ b>0 $ のとき
$ $ $ a + b ≧ 2 \sqrt{ ab } $
等号成立条件は $ a=b $
これを証明します。
【証明】
$ (左辺)^2−(右辺)^2 $
$ = ( a + b )^2−\left( 2 \sqrt{ ab } \right)^2 $
$ = a^2 +2ab + b^2−4ab $
$ = a^2 −2ab + b^2 $
$ = (a−b)^2 ≧ 0 $
∴ $ (左辺)^2≧(右辺)^2 $
$ (左辺)>0, \ (右辺)>0 $ より
$ $ $ (左辺)≧(右辺) $
等号成立条件は
$ $ $ (a−b)^2 = 0 $
∴ $ a=b $ [終]
【まとめ】「相加・相乗平均の関係」の意味
今回は「相加・相乗平均の関係」の 意味 を図形的に説明してみました。
公式の意味をしっかり理解したうえで
たくさん問題を解いて「相加・相乗平均の関係」をサクッと使えるようにしておきましょう!
「相加・相乗平均の関係」の使い方や条件、タイミングがよく分からない 「相加・相乗平均の関係」っていつ使ったらいいの? 証明問題や最小値を求める問題をわかりやすく解説してほしい! こういったお悩みを解決します。 […]
「相加・相乗平均の関係」で最大値を求める問題がよく分からない テスト・入試によく出る問題をわかりやすく解説してほしい! こういった要望に応えます。 このページでは「相加・相乗平均の関係」で 最大値 を求める[…]
質問・要望があれば気軽にコメントください👍


