微分法の「接線の方程式」の求め方がイマイチ分からない
色んな解き方のパターンがあって、どれで解いたらいいのか混乱してしまう
わかりやすく整理して教えてほしい!
こういった要望に応えます。
高校生の中にも、微分の計算はできるのに 接線の方程式を求める問題 でつまづく人は結構多いです。
「どの問題にどの解き方をしたらいいのか?」つまり「問題パターン&解き方」が整理できていないと、いざ問題を解こうとしても上手く解けずに困ってしまいます。
ですが、安心してください。
微分法 における「接線の方程式を求める問題」はたったの 3パターン!
ポイントさえ押さえれば、迷うことなくサクサク解けるようになります。
このページを読めば
- 微分法における「接線の方程式」のポイント
- 微分で「接線の方程式」を求める問題の解き方(3パターン)
を完全マスターできます。
微分 で「接線の方程式を求める問題」を解くのがニガテな人にも、図・グラフを使いながら 分かりやすく丁寧に解説 していきます!
【微分法】接線の方程式(公式)
いきなり質問です。
そもそも「微分」って何でしょうか?
まずは自分なりに考えてみてください。
・
・
・
どうですか?思い浮かびましたか?
微分 とは、ひとことで言えば「接線の傾き」です。
接線の傾きを知りたければ、とりあえず微分せよ!
ということですね。
接線の方程式(公式)
微分法における「接線の方程式」の公式として、以下をガッチリ覚えておきましょう。
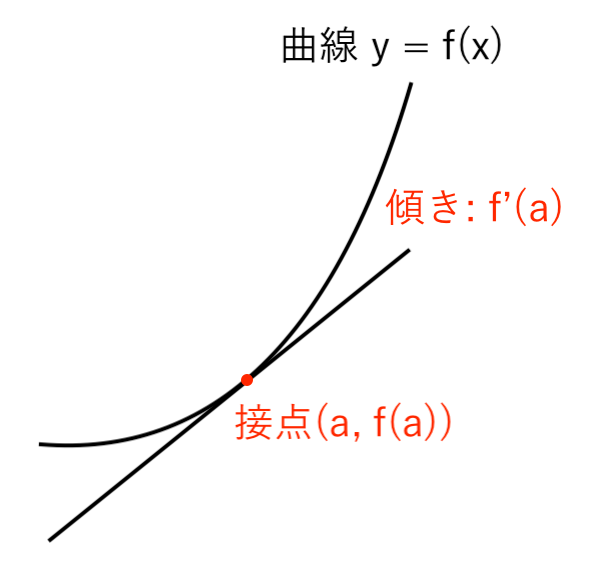
関数 $ y = f(x) $ 上の接点 $ ( a, \ f(a) ) $ における接線の方程式は
$ $ $ y − \color{red}{f(a)} = \bbox[#E2F0D9, 2pt , border:]{f'(a)} ( x − \color{red}{a} ) $
- 傾き: $\bbox[#E2F0D9, 2pt , border:]{f'(a)}$
- 接点(通る点): $ ( \color{red}{a}, \ \color{red}{f(a)} ) $
Point:「$\bbox[#E2F0D9, 2pt , border:]{傾き}$」と「接点(通る点)」が分かれば「接線の方程式」を求められる!
_2.png)
公式の意味・理由
この「接線の方程式」は、以下の2つを組み合わせることで簡単に作れます。
✔︎ 微分係数(定義)
微分係数 $f'(a)$ は、
曲線 $y=f(x)$ 上の点 $( a, \ f(a) )$($x$ 座標が $a$ である点)における「接線の傾き」
$ f'(x) $(関数 $f(x)$ を微分したもの)に $x=a$ を代入すると
$ $ $f'(a)$:接線の傾き
が分かります。
さらに、数学Ⅱ「図形と方程式」より
✔︎ 直線の方程式
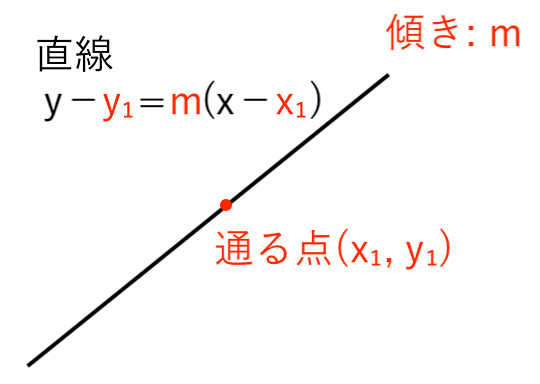
点 $( x_1, \ y_1 )$ を通り,傾き $m$ の直線の方程式は
$ $ $ y − y_1 = m ( x − x_1 ) $
これらを合わせて考えると、
関数 $ y = f(x) $ 上の接点 $ ( a, \ f(a) ) $ における接線の方程式は
$ \begin{cases}
傾き:f'(a) \\
\\
接点(通る点): ( a, \ f(a) ) \\
\end{cases}$
の直線なので
と導くことができます。
【微分法】接線の方程式の求め方 3パターン
微分法において「接線の方程式」を求める問題は、以下の3パターンに分けられます。
- 【パターン1】接点が分かる問題
- 【パターン2】傾きが分かる問題
- 【パターン3】接点も傾きも分からない問題
これらの問題パターンのうち、どれに当てはまるのか?が判断できれば、基本的に微分の問題は解くことができます。
それぞれ見ていきましょう!
【パターン1】接点が分かる問題
まずは「パターン1:接点が分かっている問題」です。
【例題1】曲線 $ y= x^3 − 5x $ 上の点 $(1, −4)$ における接線の方程式を求めよ。
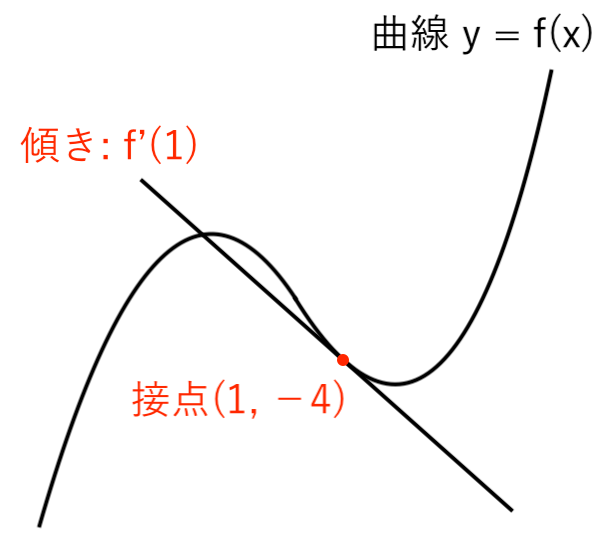
接点 $( 1 , −4)$ が分かっているので、あとは「接線の傾き」を求めれば 接線の方程式が求められますね。
解答の流れとしては、以下の通り。
- 微分する
- 接点の $x$ 座標を代入して「接線の傾き」を求める
- 接線の方程式を求める
① 微分する
まずは「$ f(x) = \ldots $ 」とおいて微分します。
【解答】
$ f(x) = x^3 − 5x $ とおくと
$ f'(x) = 3x^2 − 5x $
② 接点の $x$座標を代入して「接線の傾き」を求める
これに 接点の $x$座標($x=\color{red}{1}$)を代入すると
$ f'(\color{red}{1}) = 3 \cdot \color{red}{1}^2 − 5 \cdot \color{red}{1} $
$ $ $ = \bbox[#E2F0D9, 2pt , border:]{−2} $(接線の傾き)
③ 接線の方程式を求める
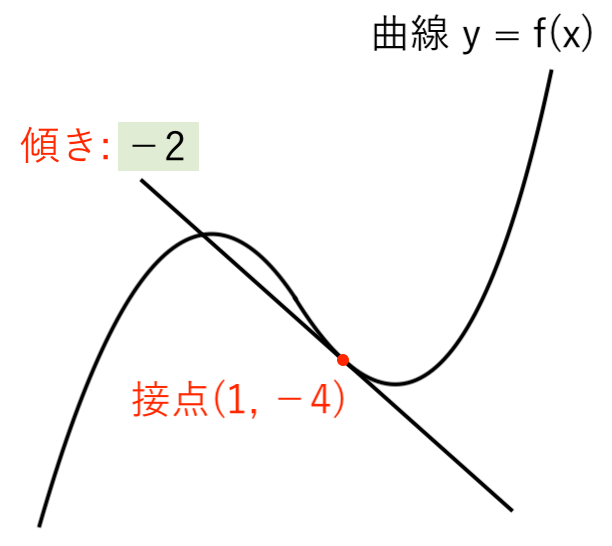
よって、求める接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{−2} \\
\\
接点(通る点):( \color{red}{1}, \ \color{red}{−4} ) \\
\end{cases}$
の直線なので
$ $ $ y − ( \color{red}{−4} ) = \bbox[#E2F0D9, 2pt , border:]{−2} ( x − \color{red}{1} ) $
∴ $ y = −2 x − 2 $
これで接線の方程式が求められました。
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ f(x) = x^3 − 5x $ とおくと
$ $ $ f'(x) = 3x^2 − 5x $
これに 接点の $x$座標($x=\color{red}{1}$)を代入すると
$ $ $ f'(\color{red}{1}) = 3 \cdot \color{red}{1}^2 − 5 \cdot \color{red}{1} $
$ $ $ = \bbox[#E2F0D9, 2pt , border:]{−2} $(接線の傾き)
よって、求める接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{−2} \\
\\
接点(通る点):( \color{red}{1}, \ \color{red}{−4} ) \\
\end{cases}$の直線なので
$ $ $ y − (\color{red}{−4}) = \bbox[#E2F0D9, 2pt , border:]{−2} ( x − \color{red}{1} ) $
∴ $ y = −2 x − 2 $
以上、「接点が分かっている問題」のパターンでした。
【パターン2】傾きが分かる問題
次は「パターン2:傾きが分かっている問題」の解き方です。
【例題2】曲線 $ y= x^3 − 2x + 5 $ において、傾きが $10$ である接線の方程式を求めよ。また、そのときの接点の座標を求めよ。
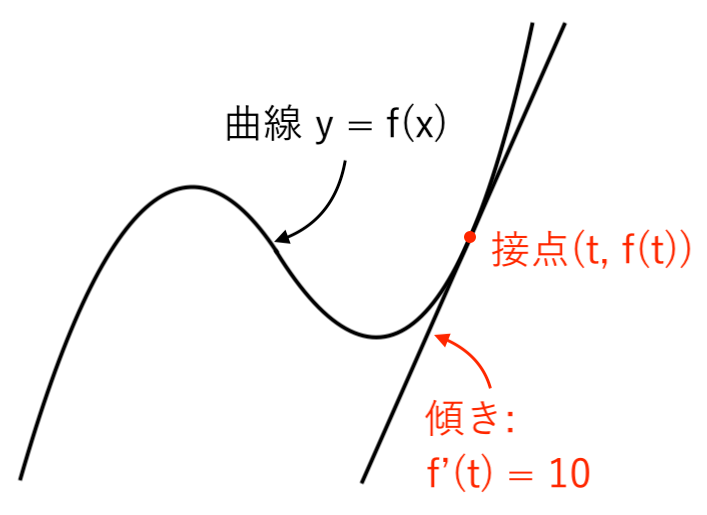
「接線の傾き」が分かっている($10$)ので、あとは「接点(通る点)」を求めれば 接線の方程式が求められますね。
解答の流れとしては、以下の通り。
- 微分する
- 接点を $( t, \ f(t) )$ とおいて「接線の傾き」を $t$ で表す
- 接線の方程式を $t$ で表す
- 「接線の傾き $=10$」を解く( $t$ を求める)
- 接線の方程式を求める
① 微分する
まずは「$ f(x) = \ldots $ 」とおいて微分します。
【解答】
$ f(x) = x^3 − 2x + 5 $ とおくと
$ f'(x) = 3x^2 − 2 $
② 接点を $( t, \ f(t) )$ とおいて「接線の傾き」を $t$ で表す
かの有名な(?)接点 tぃぃっ!の登場です。
接点を $( t, \ f(t) )$ とおくと
接線の傾きは
$ $ $ f'(t) = 3t^2 − 2 $
と表せる。
③ 接線の方程式を $t$ で表す
接点 $( t, \ f(t) )$ における 接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{ 10 } \\
\\
接点(通る点):( \color{red}{t}, \ \color{red}{f(t)} ) \\
\end{cases}$
の直線なので
$ $ $ y−\color{red}{f(t)} = \bbox[#E2F0D9, 2pt , border:]{10} ( x − \color{red}{t} ) $
∴ $ y −( t^3 − 2t + 5 ) = 10 ( x − t ) $
∴ $ y = 10 (x − t) + ( t^3 − 2t + 5 ) $
∴ $ y = 10 x + t^3 − 12t + 5 $ ・・・①
④「接線の傾き $=10$ 」を解く($t$ を求める)
「接線の傾き $=10$ 」とおいて、解いてあげると $t$ の値が求められます。
接線の傾きが $10$ なので
$ $ $ f'(t) = 10 $
∴ $ 3t^2 − 2 = 10 $
∴ $ t^2 = 4 $
∴ $ t = \pm 2 $
$t =−2, \ 2$ の2つ出てきましたが、心配せずに次に進みましょう。
⑤ 接線の方程式を求める
求めた $t$ の値を
$ $ 接線 $ y = 10 x + t^3 − 12t + 5 $ ・・・①
の式に代入すれば Finish!
これらの $t$ を 接線① に代入して
$ $[1] $t=−2$ のとき
$ $ 接線の方程式は
$ $ $ y = 10 x + (−2)^3 − 12 \cdot (−2) + 5 $
$ $ ∴ $ y = 10x + 21 $
$ $ 接点は $(−2 , f(−2) )$ ∴ $(−2 , 1)$
$ $[2] $t=2$ のとき
$ $ 接線の方程式は
$ $ $ y = 10 x + 2^3 − 12 \cdot 2 + 5 $
$ $ ∴ $ y = 10x −11 $
$ $ 接点は $(2 , f(2) )$ ∴ $(2 , 9)$
接線の方程式と同時に、接点の座標も計算しておきました。
接線の方程式が2つ出てきましたね。
傾きが $10$ の接線は、次のように 2本引けるイメージです。
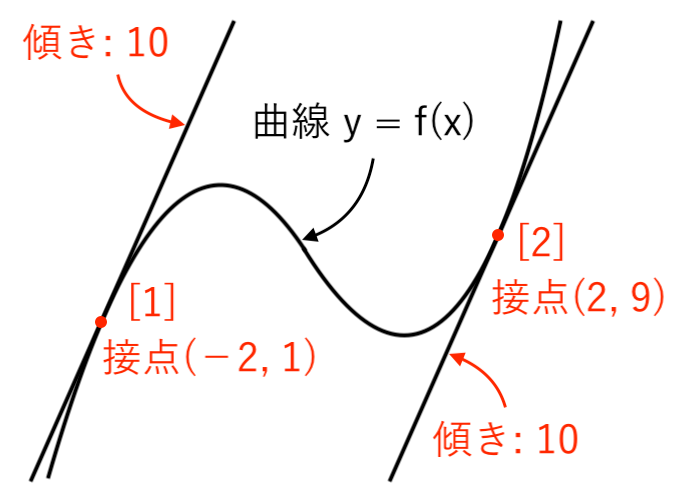
ここまでの解答をまとめておきます。
- 【解答】を見る
-
【解答】
$ f(x) = x^3 − 2x + 5 $ とおくと
$ $ $ f'(x) = 3x^2 − 2 $
また、接点を $( t, \ f(t) )$ とおくと
接線の傾きは
$ $ $ f'(t) = 3t^2 − 2 $
と表せる。
接点 $( t, \ f(t) )$ における 接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{ 10 } \\
\\
接点(通る点):( \color{red}{t}, \ \color{red}{f(t)} ) \\
\end{cases}$の直線なので
$ $ $ y−\color{red}{f(t)} = \bbox[#E2F0D9, 2pt , border:]{10} ( x − \color{red}{t} ) $
∴ $ y −( t^3 − 2t + 5 ) = 10 ( x − t ) $
∴ $ y = 10 (x − t) + ( t^3 − 2t + 5 ) $
∴ $ y = 10 x + t^3 − 12t + 5 $ ・・・①
ここで、接線の傾きが $10$ なので
$ $ $ f'(t) = 10 $
∴ $ 3t^2 − 2 = 10 $
∴ $ t^2 = 4 $
∴ $ t = \pm 2 $
これらの $t$ を 接線① に代入して
$ $[1] $t=−2$ のとき
$ $ 接線の方程式は
$ $ $ y = 10 x + (−2)^3 − 12 \cdot (−2) + 5 $
$ $ ∴ $ y = 10x + 21 $
$ $ 接点は $(−2 , f(−2) )$ ∴ $(−2 , 1)$
$ $[2] $t=2$ のとき
$ $ 接線の方程式は
$ $ $ y = 10 x + 2^3 − 12 \cdot 2 + 5 $
$ $ ∴ $ y = 10x −11 $
$ $ 接点は $(2 , f(2) )$ ∴ $(2 , 9)$
補足:手順③〜⑤ の別解
手順③〜⑤ は以下のような別解もあります。
③’ 「接線の傾き $=10$ 」を解く($t$ を求める)
$ $ ↓
④’ 接点の座標を求める
$ $ ↓
⑤’ 接線の方程式を求める
③’「接線の傾き $=10$ 」を解く($t$ を求める)
ここはさっきの手順④と同じです。
接線の傾きが $10$ なので
$ $ $ f'(t) = 10 $
∴ $ 3t^2 − 2 = 10 $
∴ $ t^2 = 4 $
∴ $ t = \pm 2 $
④’ 接点の座標を求める
2つの $ t $ の値( $ t = \pm 2 $ )について、それぞれ接点の座標を求めます。
$t = −2 $ のとき
$ $ 接点は $(−2 , f(−2) )$ ∴ $(−2 , 1)$
$t = 2 $ のとき
$ $ 接点は $(2 , f(2) )$ ∴ $(2 , 9)$
⑤’ 接線の方程式を求める
2つの接点について、それぞれ接線の方程式を求めます。
よって、求める接線の方程式は
傾きが $\bbox[#E2F0D9, 2pt , border:]{10}$ より
$ $[1] 接点 $( \color{red}{−2} , \color{red}{1})$ のとき
$ $ $ y −\color{red}{1} = \bbox[#E2F0D9, 2pt , border:]{10} \left\{ x− \color{red}{ (−2) } \right\} $ ・・・(注1)
∴ $ y = 10x + 21 $
$ $[2] 接点 $( \color{red}{2} , \color{red}{9})$ のとき
$ $ $ y −\color{red}{9} = \bbox[#E2F0D9, 2pt , border:]{10} \left( x−\color{red}{2} \right) $ ・・・(注2)
∴ $ y = 10x −11 $
(注1)$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{10} \\
\\
通る点(接点):( \color{red}{−2}, \ \color{red}{1} ) \\
\end{cases}$ の直線
(注2)$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{10} \\
\\
通る点(接点):( \color{red}{2}, \ \color{red}{9} ) \\
\end{cases}$ の直線
解き方にこだわらなくても「接線の傾き」と「通る点(接点)」が分かれば、接線の方程式はとりあえず求められるということですね。
以上、「傾きが分かっている問題」のパターンでした。
【パターン3】接点も傾きも分からない問題
最後は「パターン3:接点も傾きも分からない問題」です。
【例題3】点$(1, \ 1)$ を通り、曲線 $ y= x^3 − 4x + 5 $ に接する直線の方程式を求めよ。[12 愛媛大]
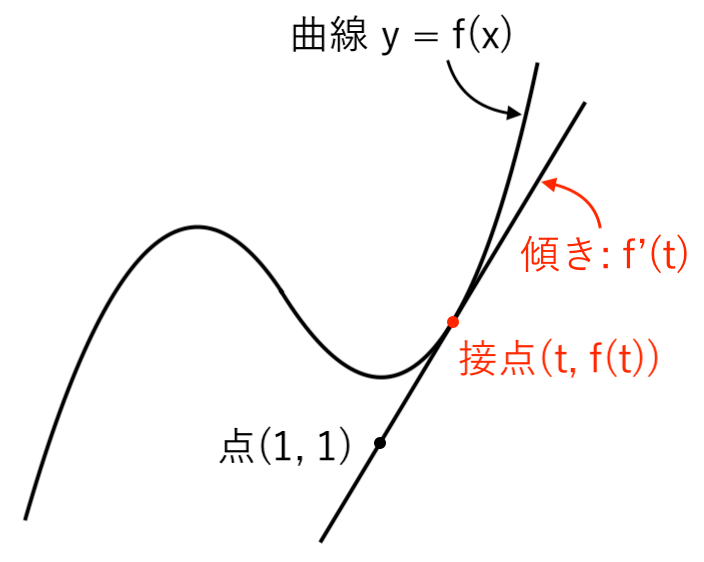
接点も傾きも分からないけど、求める直線(接線)の 通る点 $(1, \ 1)$ が分かっているので、
あとは「接線の傾き」が分かれば 接線の方程式が求められますね。
解答の流れとしては、以下の通り。
- 微分する
- 接点を $( t, \ f(t) )$ とおいて「接線の傾き」を $t$ で表す
- 接線の方程式を $t$ で表す
- ③で求めた接線に、通る点 $(1, \ 1)$ を代入する( $t$ を求める)
- 接線の方程式を求める
手順①〜③ までの流れは「パターン2」と同じですね。
① 微分する
まずは「$ f(x) = \ldots $ 」とおいて微分します。
【解答】
$ f(x) = x^3 − 4x + 5 $ とおくと
$ f'(x) = 3x^2 − 4 $
② 接点を $( t, \ f(t) )$ とおいて「接線の傾き」を $t$ で表す
接点を $( t, \ f(t) )$ とおくと
接線の傾きは
$ $ $ f'(t) = 3t^2 − 4 $
と表せる。
③ 接線の方程式を $t$ で表す
接点 $( t, \ f(t) )$ における 接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{ f'(t) } \\
\\
接点(通る点):( \color{red}{t}, \ \color{red}{f(t)} ) \\
\end{cases}$
の直線なので
$ $ $ y−\color{red}{f(t)} = \bbox[#E2F0D9, 2pt , border:]{f'(t)} ( x − \color{red}{t} ) $
∴ $ y−\left( \color{red}{t^3 − 4t + 5} \right) = \left( \bbox[#E2F0D9, 2pt , border:]{ 3t^2 − 4 } \right) ( x − \color{red}{t} ) $
∴ $ y = \left( 3t^2 − 4 \right) ( x − t ) + \left( t^3 − 4t + 5 \right) $
$ $ $ = \left( 3t^2 − 4 \right) x − t \left( 3t^2 − 4 \right) + \left( t^3 − 4t + 5 \right) $
$ $ $ = \left( 3t^2 − 4 \right) x − 2t^3 + 5 $ ・・・①
④ ③で求めた接線に、通る点 $(1, 1)$ を代入する($t$ を求める)
直線 ① は 点 $(1, \ 1)$ を通るので
$ $ $ 1 = \left( 3t^2 − 4 \right) \cdot 1 − 2t^3 + 5 $
∴ $ 1 = 3t^2 − 4 − 2t^3 + 5 $
∴ $ 2t^3 − 3t^2 = 0 $
これを $t$ の 3次方程式と見て解きます。($t$ を求める)
共通因数 $t^2$ があるのでくくり出すと
∴ $ t^2 (2t − 3) = 0 $
∴ $ \displaystyle{ t = 0, \ {3 \over 2} } $
⑤ 接線の方程式を求める
求めた $t$ の値を
$ $ 接線 $ y = \left( 3t^2 − 4 \right) x − 2t^3 + 5 $ ・・・①
の式に代入すれば Finish!
これらの $t$ を 接線① に代入して
$ $[1] $t=0$ のとき
$ $ $ y = \left( 3 \cdot 0^2 − 4 \right) x − 2 \cdot 0^3 + 5 $
$ $ $ = − 4x + 5 $
$ $[2] $\displaystyle{ t = {3 \over 2} } $ のとき
$ $ $ \displaystyle{ y = \left\{ 3 \cdot \left( {3 \over 2} \right)^2 − 4 \right\} x − 2 \cdot \left( {3 \over 2} \right)^3 + 5 } $
$ $ $ \displaystyle{ = {11 \over 4} x − {7 \over 4} } $
よって、求める接線の方程式は
$ $ $ y = − 4x + 5 , \ \displaystyle{ y = {11 \over 4} x − {7 \over 4} } $
今回も接線の方程式が2つ出てきましたね。
点 $(1, 1)$ から 曲線 $y=f(x)$ に、接線が2本引けるわけです。
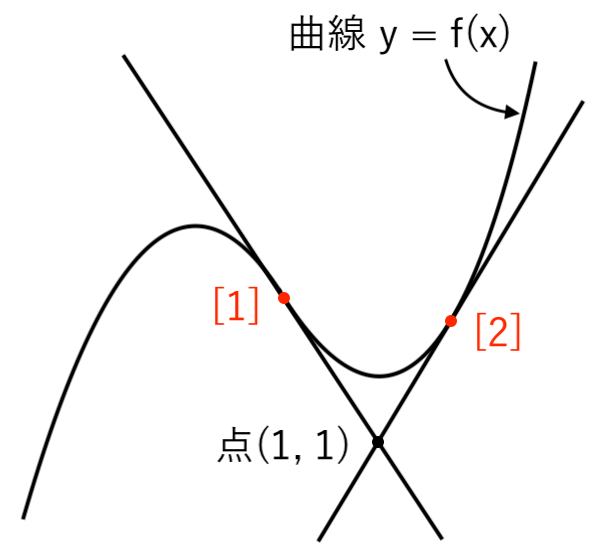
解答をまとめると、次の通り。
- 【解答】を見る
-
【解答】
$ f(x) = x^3 − 4x + 5 $ とおくと
$ $ $ f'(x) = 3x^2 − 4 $
また、接点を $( t, \ f(t) )$ とおくと
接線の傾きは
$ $ $ f'(t) = 3t^2 − 4 $
と表せる。
接点 $( t, \ f(t) )$ における 接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{ f'(t) } \\
\\
接点(通る点):( \color{red}{t}, \ \color{red}{f(t)} ) \\
\end{cases}$の直線なので
$ $ $ y−\color{red}{f(t)} = \bbox[#E2F0D9, 2pt , border:]{f'(t)} ( x − \color{red}{t} ) $
∴ $ y−\left( \color{red}{t^3 − 4t + 5} \right) = \left( \bbox[#E2F0D9, 2pt , border:]{ 3t^2 − 4 } \right) ( x − \color{red}{t} ) $
∴ $ y = \left( 3t^2 − 4 \right) ( x − t ) + \left( t^3 − 4t + 5 \right) $
$ $ $ = \left( 3t^2 − 4 \right) x − t \left( 3t^2 − 4 \right) + \left( t^3 − 4t + 5 \right) $
$ $ $ = \left( 3t^2 − 4 \right) x − 2t^3 + 5 $ ・・・①
直線 ① は 点 $(1, \ 1)$ を通るので
$ $ $ 1 = \left( 3t^2 − 4 \right) \cdot 1 − 2t^3 + 5 $
∴ $ 1 = 3t^2 − 4 − 2t^3 + 5 $
∴ $ 2t^3 − 3t^2 = 0 $
∴ $ t^2 (2t − 3) = 0 $
∴ $ \displaystyle{ t = 0, \ {3 \over 2} } $
これらの $t$ を 接線 ① の式に代入して
$ $[1] $t=0$ のとき
$ $ $ y = \left( 3 \cdot 0^2 − 4 \right) x − 2 \cdot 0^3 + 5 $
$ $ $ = − 4x + 5 $
$ $[2] $\displaystyle{ t = {3 \over 2} } $ のとき
$ $ $ \displaystyle{ y = \left\{ 3 \cdot \left( {3 \over 2} \right)^2 − 4 \right\} x − 2 \cdot \left( {3 \over 2} \right)^3 + 5 } $
$ $ $ \displaystyle{ = {11 \over 4} x − {7 \over 4} } $
よって、求める接線の方程式は
$ $ $ y = − 4x + 5 , \ \displaystyle{ y = {11 \over 4} x − {7 \over 4} } $
補足:手順⑤ の別解
手順⑤「接線の方程式を求める」は、次のように 接線① の式をあえて使わずに求める別解もあります。
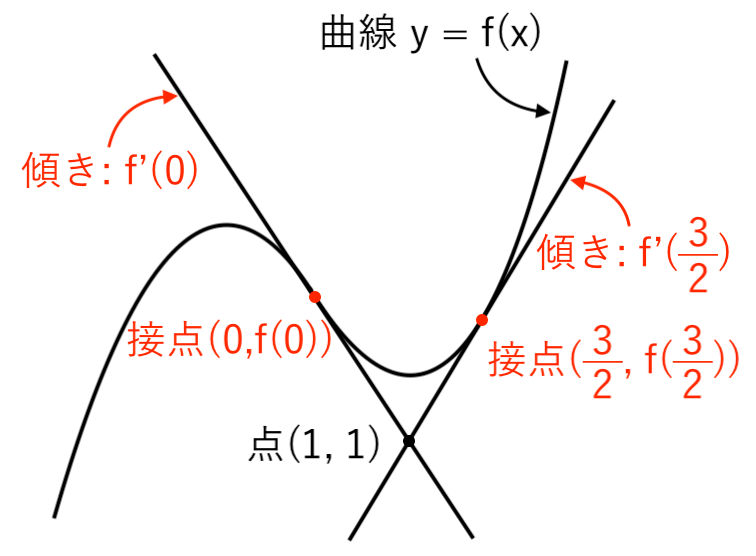
求める接線の方程式は
$ \begin{cases}
傾き:\bbox[#E2F0D9, 2pt , border:]{ f'(t) } \\
\\
通る点:( \color{red}{1}, \color{red}{1} ) \\
\end{cases}$
の直線なので
$ $[1] $t=0$ のとき
$ $ $ y − \color{red}{1} = \bbox[#E2F0D9, 2pt , border:]{ f'(0) } (x − \color{red}{1}) $
∴ $ y − 1 = \left( 3 \cdot 0^2 − 4 \right) (x − 1) $
∴ $ y = − 4 x + 5 $
$ $[2] $\displaystyle{ t = {3 \over 2} } $ のとき
$ $ $\displaystyle{ y − \color{red}{1} = \bbox[#E2F0D9, 2pt , border:]{ f’\left( {3 \over 2} \right) } (x − \color{red}{1}) } $
∴ $\displaystyle{ y − 1 = \left\{ 3 \cdot \left( {3 \over 2} \right)^2 − 4 \right\} (x − 1) } $
∴ $\displaystyle{ y − 1 = {11 \over 4} (x − 1) } $
∴ $\displaystyle{ y = {11 \over 4} x − {7 \over 4} } $
以上、「接点も傾きも分からない問題」のパターンでした。
【まとめ】微分「接線の方程式」の求め方
最後にまとめです。
微分法における「接線の方程式」の公式は、以下の通り。
関数 $ y = f(x) $ 上の接点 $ ( a, \ f(a) ) $ における接線の方程式は
$ $ $ y − \color{red}{f(a)} = \bbox[#E2F0D9, 2pt , border:]{f'(a)} ( x − \color{red}{a} ) $
- 傾き: $\bbox[#E2F0D9, 2pt , border:]{f'(a)}$
- 接点(通る点): $ ( \color{red}{a}, \ \color{red}{f(a)} ) $
Point:「$\bbox[#E2F0D9, 2pt , border:]{傾き}$」と「接点(通る点)」が分かれば「接線の方程式」を求められる!
_2.png)
微分で「接線の方程式」を求める問題は、学校のテストでも大学入試でもよく出ます。
たくさん問題を解いてスラスラ解けるようにしておきましょう!
質問・要望があれば気軽にコメントください👍
