三角関数「2倍角の公式」の覚え方を教えてほしい!
忘れてしまったときの求め方を知りたい!
「2倍角の公式」の具体的な使い方・タイミングを教えてほしい!
こういった要望に応えます。
三角関数「2倍角の公式」は 学校のテストや入試問題でも出題されやすい ので、しっかり覚えておかなければいけません。
この記事を読めば、
- 「2倍角の公式」の覚え方(簡略形)
- 「2倍角の公式」の求め方(証明のしかた)
- 「2倍角の公式」の使い方(例題で丁寧に解説)
を理解することができます。
三角関数「2倍角の公式」の覚え方【簡略形】

「2倍角の公式」は以下の通り。
- $\sin2\alpha = 2\sin\alpha \cos\alpha$
- $\cos2\alpha = \cos^2\alpha – \sin^2\alpha $
$ $ $= 2\cos^2\alpha – 1$
$ $ $= 1 – 2\sin^2\alpha$ - $\displaystyle {\tan2\alpha = {2\tan\alpha \over 1 – \tan^2\alpha}}$
「2倍角の公式」の覚え方は、語呂合わせなどもあります(後述します)が、
おすすめは「加法定理から求める(証明する)」のがベストです。
とはいえ、テスト中は時間との戦いなので、下のような簡略形で覚えておいてもOKです。
【2倍角の公式(簡略形)】
- $S = 2 s c$
- $C = c^2 – s^2$
$ $ $= 2c^2 – 1$
$ $ $= 1 – 2s^2$ - $\displaystyle {T = {2t \over 1 – t^2}}$
それぞれ簡略化して、
- $\sin2\alpha = S$(大文字)
- $\cos2\alpha = C$
- $\tan2\alpha = T$
- $\sin\alpha = s$(小文字)
- $\cos\alpha = c$
- $\tan\alpha = t$
※ ① sin「2倍角の公式」の語呂合わせ:「庭(2)に咲いた(sin)コスモス(cos)」
※ ② cos「2倍角の公式」の覚え方:「cが先、sが後、すべて2次の引き算」
三角関数「2倍角の公式」の求め方【証明】
「2倍角の公式」は 加法定理 から求められます。
- $\sin(\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha \sin\beta $
- $\cos(\alpha \pm \beta) = \cos\alpha \cos\beta \mp \sin\alpha \sin\beta $
- $\displaystyle {\tan(\alpha \pm \beta) = {\tan\alpha \pm \tan\beta \over 1 \mp \tan\alpha \tan\beta}}$
加法定理から「二倍角の公式」を求める証明をやってみましょう。
sin(サイン)「2倍角の公式」の求め方
加法定理
において、$\beta = \alpha$ とすると、
cos(コサイン)「2倍角の公式」の求め方
加法定理
において、$\beta = \alpha$ とすると、
tan(タンジェント)「2倍角の公式」の求め方
加法定理
において、$\beta = \alpha$ とすると、
これらの証明の流れを何度もイメージしておくと、自然と「2倍角の公式」が出てくるようになるはずです。
前提として、加法定理 はいつでも言えるようにしておきましょう。
加法定理 の覚え方(語呂合わせ)はこちら。
三角関数 sin cos tan「加法定理」の覚え方はないの? 加法定理の覚えやすい語呂合わせを教えてほしい! 加法定理を実際に使う問題を解きたい! こういった要望に応えます。 三角関数の「加法定理」[…]
また、三角比の相互関係 をおさらいしたい人はこちら。
「三角比の相互関係」の3つの公式が覚えられない! 簡単に暗記したり、証明する方法を知りたい! 「三角比の相互関係」をいつ使うのか、タイミングや問題を教えてほしい! こういった要望に応えます。 「三角比[…]
三角関数「2倍角の公式」の使い方【例題】
「2倍角の公式」が覚えられたところで、ここからは実際の使い方を見ていきましょう。
【例題】$\displaystyle {\sin\alpha = {1\over3}}$ $\displaystyle {\left(0<\alpha<{\pi\over2} \right)}$ のとき、次の値を求めよ。
(1) $\cos2\alpha$
(2) $\sin2\alpha$
(3) $\tan2\alpha$
(1) $\cos2\alpha$ の値を求めよ。
cos(コサイン)の「2倍角の公式」は、
- $\cos2\alpha = \cos^2\alpha – \sin^2\alpha $
- $ $ $= 2\cos^2\alpha – 1$
- $ $ $= 1 – 2\sin^2\alpha$
の3つありますが、その時々の問題によって使い分けが必要です。
今回はすでに $\sin\alpha$ の値がわかっているので、③ を使うのが一番ラクですね。
【(1)解答】
2倍角の公式より、
$\cos2\alpha = 1 – 2\sin^2\alpha$
$ $ $\displaystyle {= 1 – 2 \cdot \left( {1\over3} \right)^2}$
$ $ $\displaystyle {= {7\over9}}$
(2) $\sin2\alpha$ の値を求めよ。
解法は2つ考えられます。
- 解法1:三角比の相互関係($\cos\alpha$)→ 2倍角の公式($\sin2\alpha$)
- 解法2:三角比の相互関係($\sin2\alpha$)
せっかくなので、どっちもやってみます。
解法1
sin(サイン)の「2倍角の公式」は、
なので、$\cos\alpha$ の値がほしいところです。
そこで、$\sin\alpha$ から $\cos\alpha$ の値を求めるために、
【三角比の相互関係】
$\sin^2\alpha + \cos^2\alpha = 1$
を利用します。
【(2)解答】
$\sin^2\alpha + \cos^2\alpha = 1$ より、
$\cos^2\alpha = 1 – \sin^2\alpha$
$ $ $\displaystyle {= 1 – \left( {1\over3} \right)^2}$
$ $ $\displaystyle {= {8\over9}}$
また、$\displaystyle {0<\alpha<{\pi\over2}}$ より、
$ $ $\cos\alpha>0$ ・・・(注)
∴ $\displaystyle {\cos\alpha = \sqrt{8\over9}}$
$ $ $= \displaystyle {2\sqrt{2}\over3}$
よって、2倍角の公式より、
$\sin2\alpha = 2\sin\alpha \cos\alpha$
$ $ $=\displaystyle { 2 \cdot {1\over3} \cdot {2\sqrt{2}\over3}}$
$ $ $=\displaystyle {4\sqrt{2}\over9}$
(注)$\displaystyle {0<\alpha<{\pi\over2}}$ より、$\cos\alpha$ の符号を 単位円で確認すると
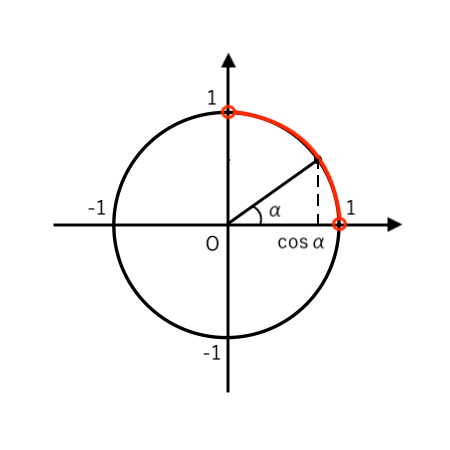
なので、$\cos\alpha>0$ とわかります。
$\cos^2\alpha$ の2乗を外すときに「正(プラス)の平方根」だけOKということです。
解法2
「三角比の相互関係」を使って、直接 $\cos2\alpha$ から $\sin2\alpha$ の値を求めることもできます。
【(2)別解】
$\sin^2 2\alpha + \cos^2 2\alpha = 1$ より、
$\sin^2 2\alpha = 1 – \cos^2 2\alpha$
$ $ $\displaystyle {= 1 – \left( {7\over9} \right)^2}$
$ $ $\displaystyle {= {32\over81}}$
また、$\displaystyle {0<\alpha<{\pi\over2}}$ より、
$ $ $\displaystyle {0<2\alpha<\pi}$
∴ $\sin2\alpha>0$ ・・・(注)
よって、
$\displaystyle {\sin 2\alpha = \sqrt{32\over81}}$
$ $ $=\displaystyle {4\sqrt{2}\over9}$
(注)$\displaystyle {0<2\alpha<\pi}$ より、$\sin 2\alpha$ の符号を 単位円で確認すると
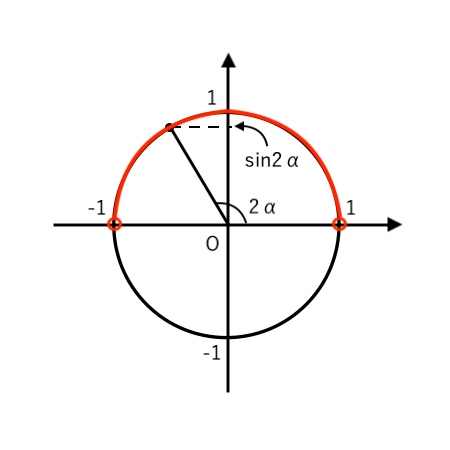
なので、$\sin 2\alpha>0$ とわかります。
$\sin^2 2\alpha$ の2乗を外すときに「正(プラス)の平方根」だけOKということになります。
(3) $\tan2\alpha$ の値を求めよ。
この問題も、2つ解法が考えられます。
- 解法1:三角比の相互関係($\tan\alpha$)→ 2倍角の公式($\tan2\alpha$)
- 解法2:三角比の相互関係($\tan2\alpha$)
どちらもやってみましょう。
解法1
tan(タンジェント)の「2倍角の公式」は、
$\displaystyle {\tan2\alpha = {2\tan\alpha \over 1 – \tan^2\alpha}}$
なので、$\tan\alpha$ の値が必要になりますね。
まずは「三角比の相互関係」から $\tan\alpha$ の値を求めます。
【(3)解答】
$\displaystyle {\tan\alpha = {\sin\alpha \over \cos\alpha}}$
$ $ $\displaystyle {= \sin\alpha \cdot {1 \over \cos\alpha}}$
$ $ $\displaystyle {= {1\over3} \cdot {3 \over 2\sqrt{2}}}$
$ $ $\displaystyle {= {1 \over 2\sqrt{2}}}$
$ $ $\displaystyle {= {\sqrt{2} \over 4}}$
よって、2倍角の公式より、
$\displaystyle {\tan2\alpha = {2\tan\alpha \over 1 – \tan^2\alpha}}$
$ $ $\displaystyle {= {\displaystyle {2 \cdot {\sqrt{2} \over 4}} \over \displaystyle {1 – \left( {\sqrt{2} \over 4} \right )^2}}}$
$ $ $\displaystyle {= { \enspace \displaystyle {\sqrt{2} \over 2} \enspace \over \displaystyle {7 \over 8}}}$
$ $ $\displaystyle {= { \displaystyle {{\sqrt{2} \over 2} × 8} \over \displaystyle {{7 \over 8} × 8}}}$ ・・・(注)
$ $ $\displaystyle {= {4 \sqrt{2}\over 7}}$
(注)分数の中に分数が入っているときは、「分母 $\left( \displaystyle{7 \over 8} \right)$ と分子 $\left( \displaystyle{\sqrt{2} \over 2} \right)$ に同じ数 $\left( 8 \right)$ をかける」と考えるといいです。
あるいは、
$ $ $\displaystyle {{ \enspace \displaystyle \color{red} {\sqrt{2} \over 2} \enspace \over \displaystyle \color{green} {7 \over 8}}}$
$ $ $= \displaystyle {\color{red} {\sqrt{2} \over 2} ÷ \color{green} {7 \over 8}}$
$ $ $= \displaystyle {{\sqrt{2} \over 2} × {8 \over 7}}$
と計算してもOK。
解法2
「三角比の相互関係」を使って、$\sin 2\alpha$ と $\cos 2\alpha$ から、いきなり $\tan 2\alpha$ の値を求めることもできます。
【(3)別解】
$\displaystyle {\tan 2\alpha = {\sin 2\alpha \over \cos 2\alpha}}$
$ $ $\displaystyle {= \sin 2\alpha \cdot {1 \over \cos 2\alpha}}$
$ $ $\displaystyle {= {4\sqrt{2}\over9} \cdot {9 \over 7}}$
$ $ $\displaystyle {= {4 \sqrt{2}\over 7}}$
やってみると分かりますが、「解法2」の方がだいぶラクでしたね。
こんな感じで色々な解法を試しておくと、テストのときに一番早い解法を使えるようになるのでオススメです。
【まとめ】三角関数「2倍角の公式」
- $\sin2\alpha = 2\sin\alpha \cos\alpha$
- $\cos2\alpha = \cos^2\alpha – \sin^2\alpha $
$ $ $= 2\cos^2\alpha – 1$
$ $ $= 1 – 2\sin^2\alpha$ - $\displaystyle {\tan2\alpha = {2\tan\alpha \over 1 – \tan^2\alpha}}$
「2倍角の公式」の覚え方は、「加法定理から求める(証明する)」のがベストです。
たくさん問題を解いて、使い方に慣れておきましょう。
質問・要望があれば気軽にコメントください👍
参考:「3倍角の公式」の覚え方
大学入試においては「3倍角の公式」も覚えておく必要があります。
三角関数「3倍角の公式」が複雑で覚えにくいな〜 「3倍角の公式」のいい覚え方(語呂合わせ)を教えてほしい! 忘れてしまったときの導出方法(証明のしかた)を知りたい! こういった要望に応えます。 三角関[…]