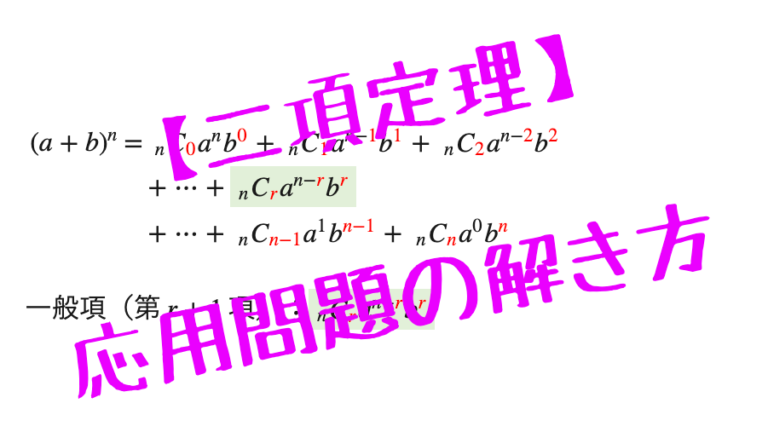二項定理の応用問題にはどんなのがあるの?
二項定理の応用問題の解き方をわかりやすく解説してほしい!
こういった要望に応えます。
二項定理のおさらい
はじめに、二項定理の公式 をおさらいしておきましょう。
$ (a + b)^n $
$= $ $ _n C_{\color{red}{0}} a^n b^{\color{red}{0}} + \ _nC_{\color{red}{1}} a^{n-{\color{red}{1}}} b^{\color{red}{1}} + \ _nC_{\color{red}{2}} a^{n-{\color{red}{2}}} b^{\color{red}{2}} \\ + \cdots + \bbox[#E2F0D9, 2pt, border:]{_nC_{\color{red}{r}} a^{n-{\color{red}{r}}} b^{\color{red}{r}} } \\ + \cdots + \ _nC_{\color{red}{n-1}} a^1 b^{\color{red}{n-1}} + \ _nC_{\color{red}{n}} a^0 b^{\color{red}{n}} $
一般項(第 $r+1$ 項):$ \bbox[#E2F0D9, 2pt, border:]{_nC_{\color{red}{r}} a^{n-{\color{red}{r}}} b^{\color{red}{r}} } $
一般項:$ \bbox[#E2F0D9, 2pt, border:]{_nC_{\color{red}{r}} a^{n-{\color{red}{r}}} b^{\color{red}{r}} } $
- 「$\color{red}{r}$」が $0$〜$n$ まで $1$ ずつ増える
- $a$ と $b$ の累乗の数字を足すと「$n$」になる
二項定理の公式・一般項がなかなか覚えられない 二項定理の使い方、応用問題の解き方をわかりやすく教えてほしい! こういったお悩みを解消します。 「二項定理の公式」を使って解く応用問題は、国公立大・私立大 に関[…]
ポイントをおさえたところで、さっそく応用問題を解いてみましょう!
二項定理 × 二項定理 の応用問題
1つ目は 二項定理 を 2つ組み合わせて 係数を求める 応用問題 です。
【例題1】$ (x+1)^8 (x-1)^4 $ の展開式における $x^{8} $ の項の係数を求めよ。 [類 14 慶應大]
まず二項定理を使って、一般項を求めておきます。
【解答】
$ (x+1)^8 $ の展開式の一般項は
$ $ $ _{8} C_{p} \cdot x^{8-p} \cdot 1^{p} $
$ $ $ = \ _{8} C_{p} \cdot x^{8-p} $ $(0≦p≦8)$
また、$ (x-1)^4 $ の展開式の一般項は
$ $ $ _{4} C_{q} \cdot x^{4-q} \cdot (-1)^{q} $
$ $ $ = \ _{4} C_{q} \cdot (-1)^{q} \cdot x^{4-q} $ $(0≦q≦4)$
よって、$ (x+1)^8 (x-1)^4 $ の展開式の一般項は
$ $ $ _{8} C_{p} \cdot x^{8-p} ×\ _{4} C_{q} \cdot (-1)^{q} \cdot x^{4-q} $
$ $ $ = \underbrace{ \bbox[#F4E2E2, 2pt, border:]{_{8} C_{p} \cdot _{4} C_{q} \cdot (-1)^{q} } }_{係数} \cdot \underbrace{ \bbox[#FFF2CC, 2pt, border:]{ x^{12-p-q} } }_{文字 \\ (変数) } $
こんな感じで $\bbox[#F4E2E2, 2pt, border:]{係数}$ と $\bbox[#FFF2CC, 2pt, border:]{文字(変数)}$を分けておきましょう。
求める条件より
$\bbox[#FFF2CC, 2pt, border:]{文字(変数)}$ について、「$x^{12-p-q}$」と「$x^8$」が一致するはずなので
$ $ $ \bbox[#FFF2CC, 2pt, border:]{ x^{\color{red}{12-p-q} } } = \bbox[#FFF2CC, 2pt, border:]{ x^\color{red}{8} } $
より
$ \color{red}{12-p-q} = \color{red}{8} $
∴ $ p+q=4 $
$0≦p≦8, \ 0≦q≦4 $ より
$ $ $ (p, \ q) = (0, \ 4), \ (1, \ 3), \ (2, \ 2), \ (3, \ 1), \ (4, \ 0) $
$ (p, \ q) $ の組み合わせが出たので、$x^8$ の項の $\bbox[#F4E2E2, 2pt, border:]{係数} \ \left( _{8} C_{p} \cdot _{4} C_{q} \cdot (-1)^{q} \right) $ は
$ _{8} C_{0} \cdot _{4} C_{4} \cdot (-1)^{4} + \ _{8} C_{1} \cdot _{4} C_{3} \cdot (-1)^{3} $ $+ \ _{8} C_{2} \cdot _{4} C_{2} \cdot (-1)^{2} $ $+ \ _{8} C_{3} \cdot _{4} C_{1} \cdot (-1)^{1} $ $+ \ _{8} C_{4} \cdot _{4} C_{0} \cdot (-1)^{0} $
$ \displaystyle { \require{cancel} = 1 − 8 \cdot 4 + { \cancel{8}^4 \cdot 7 \over \cancel{2} } \cdot { \bcancel{4}^2 \cdot 3 \over \bcancel{2} } − {8 \cdot 7 \cdot \cancel{6} \over \cancel{3 \cdot 2} } \cdot 4 }$ $ \displaystyle{ + \ { \cancel{8}^2 \cdot 7 \cdot \bcancel{6} \cdot 5 \over \cancel{4} \cdot \bcancel{3 \cdot 2} } } $
$ = 1 − 32 + 168 − 224 + 70 $
$ = −17 $
基本に忠実に解けばOKです。
二項定理 × 整数 の応用問題
2つ目は「二項定理」から整数を求めるパターンの 応用問題 です。
【例題2】$n$ を自然数とする。$ \ _nC_{0} − \ _nC_1 +\ _nC_2 − \cdots $ $+ \, (-1)^{n-1} \ _nC_{n-1} $ $+ \, (-1)^n \ _nC_n $ の値を求めよ。 [類 08 中央大]
とりあえず二項定理の展開式を書き出して、考えてみましょう。
【解答】
二項定理より
$ $ $ (a + b)^n $
$= $ $ _n C_{\color{red}{0}} a^n b^{\color{red}{0}} + \ _nC_{\color{red}{1}} a^{n-{\color{red}{1}}} b^{\color{red}{1}} + \ _nC_{\color{red}{2}} a^{n-{\color{red}{2}}} b^{\color{red}{2}} \\ + \cdots + \ _nC_{\color{red}{n-1}} a^1 b^{\color{red}{n-1}} + \ _nC_{\color{red}{n}} a^0 b^{\color{red}{n}} $
一方、与式をちょっと変形して
$ $ $ \ _n C_0 − \ _nC_1 + \ _nC_{2} − \cdots + (−1)^{n-1} \ _nC_{n-1} \\ + (−1)^{n} \ _nC_{n} $
$ $ $ =$ $ _n C_0 + \ _nC_1 (−1) + \ _nC_{2} + \cdots + \ _nC_{n-1} (−1)^{n-1} \\ + \ _nC_{n} (−1)^{n} $
と見比べると・・・
$a=1, \ b= −1 $ とすると
$ $ $ (1 − 1)^n $
$= $ $ _n C_0 1^n (−1)^0 + \ _nC_1 1^{n-1} (−1)^{1} \\ + \ _nC_{2} 1^{n-2} (−1)^{2} + \cdots \\ + \ _nC_{n-1} 1^1 (−1)^{n-1} + \ _nC_{n} 1^0 (−1)^{n} $
∴ $ \ _n C_0 − \ _nC_1 + \ _nC_{2} − $ $ \cdots + (−1)^{n-1} \ _nC_{n-1} $ $ + (−1)^{n} \ _nC_{n} = 0 $
こんな感じで、うまく求められました。
【例題3】$m$ を自然数とする。$ \ _mC_{0} + \ _mC_1 $ $+\ _mC_2 + \cdots $ $+ \ _mC_{m-1} $ $+ \ _mC_m $ の値を求めよ。 [11 関西大]
これも【例題2】と同様に解きます。
【解答】
二項定理より
$ $ $ (a + b)^m $
$= $ $ _m C_{\color{red}{0}} a^n b^{\color{red}{0}} + \ _mC_{\color{red}{1}} a^{m-{\color{red}{1}}} b^{\color{red}{1}} + \ _mC_{\color{red}{2}} a^{m-{\color{red}{2}}} b^{\color{red}{2}} \\ + \cdots + \ _mC_{\color{red}{m-1}} a^1 b^{\color{red}{m-1}} + \ _nC_{\color{red}{m}} a^0 b^{\color{red}{m}} $
$a=1, \ b=1$ とすると
$ $ $ (1 + 1)^m $
$= $ $\ _m C_0 1^m \cdot 1^{0} + \ _mC_{1} 1^{m-1} \cdot 1^{1} \\ + \ _mC_{2} 1^{m-2} \cdot 1^{2} + \cdots \\ + \ _mC_{m-1} 1^1 \cdot 1^{m-1} + \ _nC_{m} 1^0 \cdot 1^{m} $
∴ $ \ _mC_{0} + \ _mC_1 +\ _mC_2 + \cdots $ $+ \ _mC_{m-1} $ $+ \ _mC_m = 2^m $
【例題1、2】は入試問題でよく出るパターンなので、必ずマスターしておきましょう!
二項定理 × 最大値 の応用問題
3つ目は「二項定理」と「最大値」を融合した 応用問題 です。
【例題4】$ (x+2)^{10} $ の展開式における最大の係数を求めよ。 [神奈川大]
二項定理で「係数」を求めるパターンの問題 では、一般項を利用します。
$ (a + b)^n $ の展開式の一般項は
$ $ $ _nC_{\color{red}{r}} \cdot a^{n-{\color{red}{r}}} \cdot b^{\color{red}{r}} $ $(0≦r≦n)$
【解答】
$ (x+2)^{10} $ の展開式における一般項は
$ $ $ _{10} C_{r} \cdot x^{10-r} \cdot 2^{r} $
$ = \underbrace{ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } }_{係数} \cdot \underbrace{ \bbox[#FFF2CC, 2pt, border:]{ x^{10-r} } }_{文字 \\ (変数) } $
いつも通り $\bbox[#F4E2E2, 2pt, border:]{係数}$ と $\bbox[#FFF2CC, 2pt, border:]{文字(変数)}$を分けておきます。
次に、$\bbox[#F4E2E2, 2pt, border:]{係数}$ の部分を 関数 $f(r)$ とおきます。
$ \displaystyle{ f(r) = \ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } } $ とすると
$ \displaystyle{ f(r) = {10! \cdot 2^{r} \over r! \, (10-r)!} } $ $(0≦r≦10)$
(注)$ \displaystyle{ _n C_r = {_n P_r \over r!} = { n! \over r! \, (n−r)!} } $ $\left( 0≦r≦n \right)$
ここからは「確率の最大値」を求めるパターンの問題と同じ解法を使います。
「確率Pnが最大になるnの値」を求める問題がイマイチわからない 「玉やカードを同時に(一度に)取り出す問題」「サイコロとかの反復試行の問題」で一番ラクな解き方をわかりやすく教えてほしい! こういったお悩みを解消します。 &nb[…]
関数 $f(r)$ の最大値を求めるために、$f(r+1)$ を出しておきましょう。
$f(r)$ の式の「$r$」を「$r+1$」に置き換えます。($r$ の数字が 1つ増える)
$ \displaystyle{ f(r+1) = {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!} } $ $(0≦r≦9)$
(注)「$10−r$」→ $ 10−(r+1) = 9−r $
ここから $f(r)$ の最大値 を求める方法は、以下の 2通りあります。
- 差「$ f(r+1)−f(r)>0 $」となる $r$ を求める
- 比「$ \displaystyle{ { f(r+1) \over f(r) } > 1 } $」となる $r$ を求める
せっかくなので両方やってみます。
解き方① $ f(r+1)−f(r)>0 $ となる $r$ を求める
$ f(r+1)−f(r) $
$ \displaystyle{ = {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!}−{10! \cdot 2^{r} \over r! \, (10-r)!} } $
(無理やり)分母を揃えると
$ \displaystyle{ = {10! \cdot 2^{r+1} \cdot \color{red}{ (10-r) } \over (r+1)! \, \color{red}{ (10-r) } \, (9-r)!}−{10! \cdot 2^{r} \cdot \color{red}{ (r+1) } \over \color{red}{ (r+1) } \ r! \, (10-r)!} } $
$ \displaystyle{ = {10! \cdot 2^{r+1} \cdot (10-r) \over (r+1)! \, (10-r)!}−{10! \cdot 2^{r} \cdot (r+1) \over (r+1)! \, (10-r)!} } $
(無理やり)共通因数をくくり出すと
$ \displaystyle{ = {10! \cdot 2^{r} \over (r+1)! \, (10-r)!} \cdot \left\{ 2 (10-r) − (r+1) \right\} } $
$ \displaystyle{ = {10! \cdot 2^{r} \over (r+1)! \, (10-r)!} \cdot \left( \bbox[#F4E2E2, 2pt, border:]{ 19-3r } \right) } $ $(0≦r≦9)$
ここで
$ $ $ \displaystyle{ \color{red}{ f(r+1) − f(r) > 0 } } $
とすると、$ 0≦r≦9 $ より、常に
$ $ $ \displaystyle{ {10! \cdot 2^{r} \over (r+1)! \, (10-r)!} >0 } $
なので、結局
$ $ $ \bbox[#F4E2E2, 2pt, border:]{ 19-3r }> 0 $
であればよいわけです。
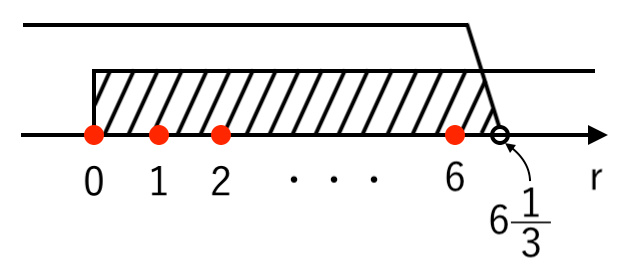
$ $∴ $ \displaystyle{ r <{19 \over 3} = 6{1 \over 3} } $
$r$ は $0≦r≦9$ をみたす整数なので
$ $ $ \color{red}{r = 0, 1, 2, \cdots , 6} $
よって
逆に
$ $ $ \color{red}{ f(r+1)−f(r) < 0 } $
とすると、不等号の向きが逆になるので
$ $ $ \displaystyle{ r > {19 \over 3} = 6{1 \over 3} } $
$ $∴ $ \color{red}{r = 7, 8, 9} $
よって
まとめて書くと
r = 0, 1, 2, \cdots , 6 \enspace \, のとき \, \, f(r)<f(r+1) \, (単調増加)\\
\\
r = 7, 8, 9 \enspace \enspace \enspace \enspace \enspace \, \, のとき \, \, f(r)>f(r+1) \, (単調減少)\\
\end{cases}$
ゆえに
なので
$f(r)$ の最大値(求める最大の係数)は
$ $ $ \displaystyle{ \color{red}{f(7)} = {10! \cdot 2^{7} \over 7! \cdot 3!} } $
$ $ $ \displaystyle{ = \require{cancel} {10 \cdot \displaystyle{ \mathop{ \bcancel{9} }^3 } \cdot \mathop{ \cancel{8} }^4 \cdot \cancel{7!} \cdot 2^{7} \over \cancel{7!} \cdot \bcancel{3} \cdot \cancel{2} } } $
$ $ $ = 15360 $
「解き方①」の解答をまとめると、こんな感じ。
- 【解答①】を見る
-
【解答①】
$ (x+2)^{10} $ の展開式における一般項は
$ $ $ _{10} C_{r} \cdot x^{10-r} \cdot 2^{r} $
$ = \underbrace{ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } }_{係数} \cdot \underbrace{ \bbox[#FFF2CC, 2pt, border:]{ x^{10-r} } }_{文字 \\ (変数) } $
$ \displaystyle{ f(r) = \ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } } $ とすると
$ $ $ \displaystyle{ f(r) = {10! \cdot 2^{r} \over r! \, (10-r)!} } $ $(0≦r≦10)$
∴ $ \displaystyle{ f(r+1) = {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!} } $ $(0≦r≦9)$
ここで
$ $ $ f(r+1)−f(r) $
$ \displaystyle{ = {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!}−{10! \cdot 2^{r} \over r! \, (10-r)!} } $
$ \displaystyle{ = {10! \cdot 2^{r} \over (r+1)! \, (10-r)!} \cdot \left\{ 2 (10-r) − (r+1) \right\} } $
$ \displaystyle{ = {10! \cdot 2^{r} \over (r+1)! \, (10-r)!} \cdot \left( \bbox[#F4E2E2, 2pt, border:]{ 19-3r } \right) } $ $(0≦r≦9)$
∴ $ \begin{cases}
r = 0, 1, 2, \cdots , 6 \enspace \, のとき \, \, f(r)<f(r+1) \\
\\
r = 7, 8, 9 \enspace \enspace \enspace \enspace \enspace \, \, のとき \, \, f(r)>f(r+1) \\
\end{cases}$∴ $ f(0)<f(1)<f(2)<\cdots $ $<f(6)<\color{red}{f(7)}>f(8) $ $>f(9)>f(10) $
よって、$f(r)$ の最大値(求める最大の係数)は
$ $ $ \displaystyle{ \color{red}{f(7)} = {10! \cdot 2^{7} \over 7! \cdot 3!} } $
$ $ $ \displaystyle{ = \require{cancel} {10 \cdot \displaystyle{ \mathop{ \bcancel{9} }^3 } \cdot \mathop{ \cancel{8} }^4 \cdot \cancel{7!} \cdot 2^{7} \over \cancel{7!} \cdot \bcancel{3} \cdot \cancel{2} } } $
$ $ $ = 15360 $
解き方② $ \displaystyle{ { f(r+1) \over f(r) } > 1 } $ となる $r$ を求める
$ \displaystyle{ { f(r+1) \over f(r) } } $
$ \displaystyle{ = { f(r+1) ×{1 \over f(r)} } } $
$ \displaystyle{ = { {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!}×{ r! \, (10-r)! \over {10! \cdot 2^{r} } } } } $
$ \displaystyle{ = { { \require{cancel} \cancel{10!} \cdot \bcancel{2^{r}} \cdot 2 \over (r+1) \ \bcancel{r!} \ \cancel{(9-r)!} }×{ \bcancel{r!} \ (10-r) \ \cancel{(9-r)!} \over { \cancel{10!} \cdot \bcancel{2^{r}} } } } } $
$ \displaystyle{ = { { 2 (10-r) \over r+1 } } } $ $(0≦r≦9)$
ここで
$ $ $ \displaystyle{ \color{red}{ { f(r+1) \over f(r) } > 1 } } $
とすると
$ $ $ \displaystyle{ { 2 (10-r) \over r+1 } > 1 } $
両辺に $(r+1) \ (>0)$ をかけて
$ $ $ 2 (10-r) > r+1 $
$ $∴ $ 20-2r > r+1 $
$ $∴ $ \displaystyle{ r < {19 \over 3} = 6{1 \over 3} } $
$r$ は $0≦r≦9$ をみたす整数なので
$ $ $ \color{red}{r = 0, 1, 2, \cdots , 6} $
よって
逆に
$ $ $ \displaystyle{ \color{red}{ { f(r+1) \over f(r) } < 1 } } $
とすると、不等号の向きが逆になるので
$ $ $ \displaystyle{ r > {19 \over 3} = 6{1 \over 3} } $
$ $∴ $ \color{red}{r = 7, 8, 9} $
よって
ここまで出来たら、あとは「解き方①」と同様です。
r = 0, 1, 2, \cdots , 6 \enspace \, のとき \, \, f(r)<f(r+1) \, (単調増加)\\
\\
r = 7, 8, 9 \enspace \enspace \enspace \enspace \enspace \, \, のとき \, \, f(r)>f(r+1) \, (単調減少)\\
\end{cases}$
ゆえに
なので
$f(r)$ の最大値(求める最大の係数)は
$ $ $ \color{red}{f(7)} = \cdots = 15360 $
以上です。
「解き方②」の解答をまとめると、こんな感じ。
- 【解答②】を見る
-
【解答②】
$ (x+2)^{10} $ の展開式における一般項は
$ $ $ _{10} C_{r} \cdot x^{10-r} \cdot 2^{r} $
$ = \underbrace{ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } }_{係数} \cdot \underbrace{ \bbox[#FFF2CC, 2pt, border:]{ x^{10-r} } }_{文字 \\ (変数) } $
$ \displaystyle{ f(r) = \ \bbox[#F4E2E2, 2pt, border:]{_{10} C_{r} \cdot 2^{r} } } $ とすると
$ $ $ \displaystyle{ f(r) = {10! \cdot 2^{r} \over r! \, (10-r)!} } $ $(0≦r≦10)$
∴ $ \displaystyle{ f(r+1) = {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!} } $ $(0≦r≦9)$
ここで
$ $ $ \displaystyle{ { f(r+1) \over f(r) } } $
$ \displaystyle{ = { f(r+1) ×{1 \over f(r)} } } $
$ \displaystyle{ = { {10! \cdot 2^{r+1} \over (r+1)! \, (9-r)!}×{ r! \, (10-r)! \over {10! \cdot 2^{r} } } } } $
$ \displaystyle{ = { { 2 (10-r) \over r+1 } } } $ $(0≦r≦9)$
∴ $ \begin{cases}
r = 0, 1, 2, \cdots , 6 \enspace \, のとき \, \, f(r)<f(r+1) \\
\\
r = 7, 8, 9 \enspace \enspace \enspace \enspace \, \, のとき \, \, f(r)>f(r+1) \\
\end{cases}$∴ $ f(0)<f(1)<f(2)<\cdots $ $<f(6)<\color{red}{f(7)}>f(8)$ $>f(9)>f(10) $
よって、$f(r)$ の最大値(求める最大の係数)は
$ $ $ \color{red}{f(7)} = \cdots = 15360 $
以上です。お疲れ様でした!
二項定理 × 数列 の応用問題
リンク準備中
二項定理 × 証明 の応用問題
リンク準備中