「三角比の相互関係」の3つの公式が覚えられない!
簡単に暗記したり、証明する方法を知りたい!
「三角比の相互関係」をいつ使うのか、タイミングや問題を教えてほしい!
こういった要望に応えます。
「三角比の相互関係」は、三角比をマスターする上で必ず覚えておかなければいけない 重要な公式 です。
この記事では、
- 「三角比の相互関係」の公式3つの覚え方
- 「三角比の相互関係」の公式の証明
- 「三角比の相互関係」をいつ使うのか?(例題で解説)
を、学校や他のサイトでは教えてくれないような 本質やポイントだけを 超シンプルに説明 します!
「三角比の相互関係」の公式3つとは?

「三角比の相互関係」の公式とは、次の3つのことを言います。
- $\sin^2 \theta + \cos^2 \theta = 1$
- $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
- $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
「三角比の相互関係」は、一見すると覚えにくいですが、公式の意味 を理解すれば自然と覚えられるようになります。
心配しなくても大丈夫!
このページを読み終える頃には、これらの公式が自然とスラスラ出てくるくらい 超わかりやすく&シンプルに解説します!
「三角比の相互関係」の覚え方【簡単に言うと○○】
「三角比の相互関係」の簡単な覚え方を、図を使って説明します。
公式① $\sin^2 \theta + \cos^2 \theta = 1$
この公式は、簡単に言うと「三平方の定理」です。
まず、単位円 をイメージしましょう。
単位円は「原点Oが中心、半径1の円」でしたね。

単位円上の点をPとすると、
$ $ P$ (\cos\theta , \sin \theta )$
$ $ OP = $1$(半径)
になります。
すると、このような直角三角形が見えます。
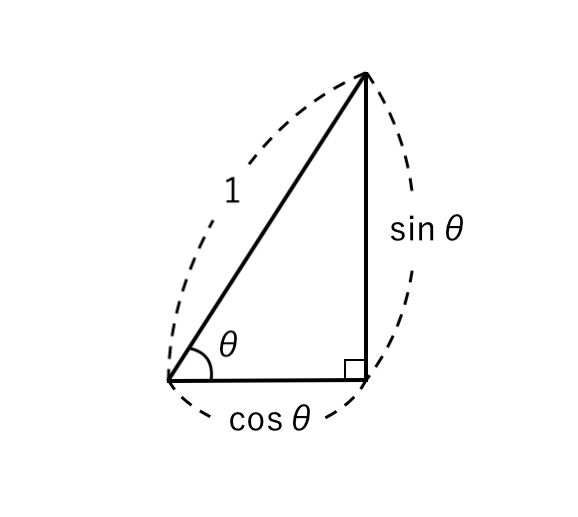
ここに、三平方の定理 を使うと
$ $ $\sin^2 \theta + \cos^2 \theta = 1^2 $
よって、
が作れました。
この流れとイメージで覚えましょう。
公式② $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
次は「公式②」です。
そもそもですが、「tan(タンジェント)」とは何でしょうか?
・
・
・
ひとことで言うと、
tan(タンジェント)は「傾き」のことです。
中学で習った直線の式(一次関数とか比例)を思い出すと、

例えば、右に 2 、上に 3 進む直線の傾きは
$ $ $ \displaystyle { \color{red} {3} \over \color{green} {2}} $
になります。
先ほどの直角三角形をイメージすると、
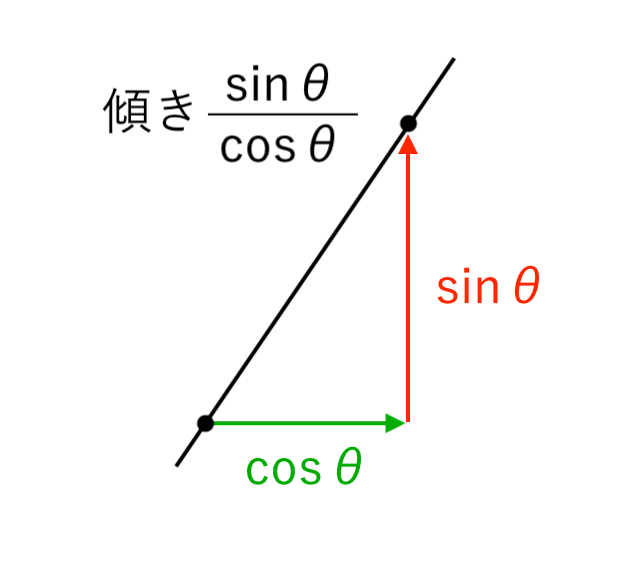
右に $ \color{green} { \cos \theta } $ 、上に $ \color{red} { \sin \theta } $ 進む直線の傾き($ \tan \theta $)は
$ $ $ \displaystyle { \color{red} { \sin \theta } \over \color{green} { \cos \theta } } $
なので、
が言えました。
公式③ $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
結論を言うと、「公式③」は暗記する必要がありません。
公式①と②から、すぐに求められるからです。
証明のしかたは後述します。
「三角比の相互関係」の公式【証明】
「三角比の相互関係」の公式を証明しましょう。
先ほどは話を分かりやすくしたかったので、単位円で(斜辺が $1$ の直角三角形で)説明しました。
ここではちゃんと一般化して証明したいので、斜辺を $ \color{red} {r} $ $(>0)$とおくことにします。
公式① $\sin^2 \theta + \cos^2 \theta = 1$ の証明
【証明】
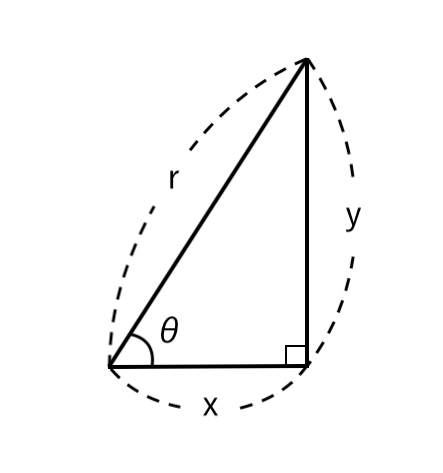
上図のような直角三角形を考える。
三角比の定義より
$ \begin{cases}
\displaystyle { \cos \theta = { x \over r } } \\
\\
\displaystyle { \sin \theta = { y \over r } } \\
\end{cases} $
それぞれ両辺に $r$ をかけて
$ \begin{cases}
r\cos \theta = x \enspace・・・① \\
\\
r\sin \theta = y \enspace・・・② \\
\end{cases} $
また、三平方の定理より
$ $ $ x^2 + y^2 = r^2 $
①、②を代入して
$ $ $ ( r \cos \theta )^2 + ( r \sin \theta )^2 = r^2 $
$ $ ∴ $ r^2 \cos^2 \theta + r^2 \sin^2 \theta = r^2 $
両辺を $r^2$ で割って
$ $ $ \cos^2 \theta + \sin^2 \theta = 1 $
よって
$ $ $ \sin^2 \theta + \cos^2 \theta = 1 $ [終]
公式② $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$ の証明
【証明】
三角比の定義より
$ $ $ \displaystyle { \tan \theta = { y \over x } }$
①、②を代入して
$ $ $ \displaystyle { \tan \theta = { r\sin \theta \over r\cos \theta } }$
$ $ $ \displaystyle { = { \sin \theta \over \cos \theta } }$ [終]
公式③ $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $ の証明
さきほど、公式③の覚え方のところでスキップした話です。
公式①と②を変形することで簡単に導けます。
【証明】
公式① $ \sin^2 \theta + \cos^2 \theta = 1 $
の両辺を $ \cos^2 \theta $ で割ると
$ $ $ \displaystyle { { \sin^2 \theta \over \cos^2 \theta } + { \cos^2 \theta \over \cos^2 \theta } = { 1 \over \cos^2 \theta } } $
$ $ ∴ $ \displaystyle { \left( { \sin \theta \over \cos \theta } \right)^2 + 1 = { 1 \over \cos^2 \theta } } $
公式② $\displaystyle { { \sin \theta \over \cos \theta } = \tan \theta }$ を代入して
$ $ $ \displaystyle { \tan^2 \theta + 1 = { 1 \over \cos^2 \theta } } $
よって
$ $ $ \displaystyle { 1 + \tan^2 \theta = { 1 \over \cos^2 \theta } } $ [終]
これで「三角比の相互関係」の公式の証明が終わりました。
公式③の証明はいつでも導けるように、流れをしっかり覚えておきましょう。
「三角比の相互関係」をいつ使うか?【例題】
「三角比の相互関係」をいつ使うのか?を体感するために、例題を見てみましょう。
【例題】$\theta$ は鋭角とする。三角比の1つが次の値をとるとき、他の2つの三角比の値を求めよ。
(1) $ \displaystyle { \sin \theta = { 2 \over 3 } } $
(2) $ \tan \theta = \sqrt{2} $
こんな感じの問題で「三角比の相互関係」を使うと、
というわけです。
実際にやってみましょう!
(1) $ \displaystyle { \sin \theta = { 2 \over 3 } } $
- $\sin^2 \theta + \cos^2 \theta = 1$
- $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
- $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
手順としては、
【公式①】$\sin \theta $ から $\cos \theta $ を求める
【公式②】$\sin \theta $、$\cos \theta $ から $\tan \theta $ を求める
というのがスムーズです。
もちろん前半で
$ $ 【公式③】$\sin \theta $ から $\tan \theta $ を求める
というのもアリですが、なるべく簡単な計算がいいですよね?
なので、「公式①」を使った方がいいと判断できるわけです。
【解答】
$ $ $\sin^2 \theta + \cos^2 \theta = 1$
に $ \displaystyle { \sin \theta = { 2 \over 3 } } $ を代入して
$ $ $ \displaystyle { \left( { 2 \over 3 } \right)^2 + \cos^2 \theta = 1 } $
$ $ ∴ $\displaystyle { { 4 \over 9 }+ \cos^2 \theta = 1 } $
$ $ ∴ $\displaystyle { \cos^2 \theta = { 5 \over 9 } } $
ここで、$\theta$ は鋭角 $\displaystyle { \left( 0^\circ<\theta<90^\circ \right) }$ より
$ $ $\cos\theta>0$ ・・・(注)
∴ $\displaystyle {\cos\theta = \sqrt{ 5 \over 9 } }$
$ $ $= \displaystyle { \sqrt{5}\over 3 } $
また、
$ $ $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
$ $ $\displaystyle { = \sin \theta \cdot {1 \over \cos \theta} }$
$ $ $\displaystyle { = { 2 \over 3 } \cdot { 3 \over \sqrt{5} } }$
$ $ $\displaystyle { = { 2 \over \sqrt{5} } }$
$ $ $\displaystyle { = { 2 \sqrt{5} \over 5 } }$
(注)$\theta$ は鋭角 $\displaystyle { \left( 0^\circ <\theta<90^\circ \right) }$ より、$\cos\theta$ の符号を 単位円で確認すると
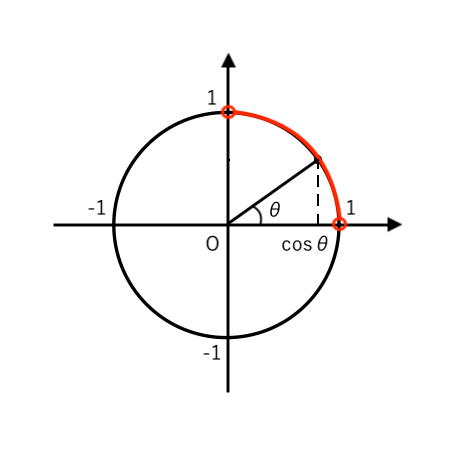
なので、$\cos\theta>0$ とわかります。
$\cos^2\theta$ の2乗を外すときに「正(プラス)の平方根」だけOKということですね。
(2) $ \tan \theta = \sqrt{2} $
今度は $ \tan \theta = \sqrt{2} $ が与えられているので、
【公式③】$\tan \theta $ から $\cos \theta $ を求める
【公式②】$\tan \theta $、$\cos \theta $ から $\sin \theta $ を求める
という流れが一番ラクかな〜と思います。
後半は別解もあるので、後述します。
【解答】
$ $ $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $
に $ \tan \theta = \sqrt{2} $ を代入して
$ $ $\displaystyle { 1 + (\sqrt{2})^2 = {1 \over \cos^2 \theta} } $
$ $ ∴ $\displaystyle { {1 \over \cos^2 \theta} = 3} $
両辺の逆数をとって
$ $ $\displaystyle { \cos^2 \theta = { 1 \over 3 } } $
ここで、$\theta$ は鋭角 $\displaystyle { \left( 0^\circ <\theta<90^\circ \right) }$ より
$ $ $\cos\theta>0$
∴ $\displaystyle {\cos\theta = \sqrt{ 1\over 3 } }$
$ $ $= \displaystyle { 1 \over \sqrt{3} } $
$ $ $= \displaystyle { \sqrt{3} \over 3 } $
また、
$ $ $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$ ・・・(注)
の両辺に $ \cos \theta $ をかけて
$ $ $\displaystyle { \tan \theta \cdot \cos \theta = {\sin \theta \over \require{cancel} \bcancel{ \cos \theta } } \cdot \bcancel{ \cos \theta } }$
左辺と右辺を入れ替えて
$ $ $\displaystyle { \sin \theta = \tan \theta \cdot \cos \theta }$
$ $ $\displaystyle { = \sqrt{2} \cdot { \sqrt{3} \over 3 } }$
$ $ $\displaystyle { = {\sqrt{6} \over 3 } } $
(注)ここからの別解として、
$ $ 【公式①】$ \cos\theta $ から $ \sin\theta $ を求める
$ $ もアリですね。
【別解】
$ $ $\sin^2 \theta + \cos^2 \theta = 1$
に $\displaystyle {\cos\theta = { \sqrt{3} \over 3 } }$ を代入して
$ $ $\displaystyle { \sin^2 \theta + \left({ \sqrt{3} \over 3 } \right)^2 = 1 } $
$ $ ∴ $\displaystyle { \sin^2 \theta + { 1 \over 3 } = 1 } $
$ $ ∴ $\displaystyle { \sin^2 \theta = { 2 \over 3 } } $
ここで、$\theta$ は鋭角 $\displaystyle { \left( 0^\circ <\theta<90^\circ \right) }$ より
$ $ $\sin \theta>0$ ・・・(注)
∴ $\displaystyle {\sin\theta = \sqrt{ 2\over 3 } }$
$ $ $= \displaystyle { \sqrt{6} \over 3 } $
(注)$\theta$ は鋭角 $\displaystyle { \left( 0^\circ <\theta<90^\circ \right) }$ より、$\sin\theta$ の符号を 単位円で確認すると
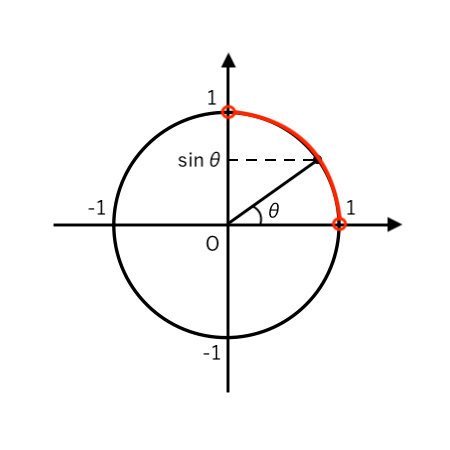
なので、$\sin\theta>0$ とわかります。
$\sin^2\theta$ の2乗を外すときに「正(プラス)の平方根」だけOKということですね。
【まとめ】「三角比の相互関係」の公式の覚え方
改めて、「三角比の相互関係」の公式3つの覚え方をまとめておきます。
- $\sin^2 \theta + \cos^2 \theta = 1$
- $\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
- $\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $

上のような直角三角形をイメージして、
【公式①】三平方の定理
【公式②】直線の傾き
【公式③】①と②を変形して導く
で「三角比の相互関係」を覚えましょう!
質問・要望があれば気軽にコメントください👍
「三角比の相互関係」公式なしで簡単に求める「裏ワザ」
「三角比の相互関係」を公式を使わず、一瞬で&簡単に求める「裏ワザ」もあります。
sin cos tanを求めるときに「三角比の相互関係」の公式をいちいち使うのが面倒だ・・・ 「三角比の相互関係」の公式3つを使わずに、サクッと簡単に計算する方法が知りたい! こういった要望に応えます。 […]

