三角関数「3倍角の公式」が複雑で覚えにくいな〜
「3倍角の公式」のいい覚え方(語呂合わせ)を教えてほしい!
忘れてしまったときの導出方法(証明のしかた)を知りたい!
こういった要望に応えます。
三角関数「3倍角の公式」は 入試問題でも出やすいため、バッチリ覚えておく必要があります。
にも関わらず、形が複雑で覚えにくく、多くの高校生や受験生を悩ませています。
そこで今回は、
- 「3倍角の公式」の覚え方(語呂合わせ)
- 「3倍角の公式」の導出方法(証明のしかた)
- 「3倍角の公式」の使い方(例題で丁寧に解説)
をわかりやすく丁寧に解説します。
「3倍角の公式」の覚え方【語呂合わせ】
覚えておくべき「3倍角の公式」はこちら。
- $\sin 3\alpha = 3\sin \alpha – 4\sin^3 \alpha$
- $\cos 3\alpha = -3\cos \alpha + 4\cos^3 \alpha$
※ tan(タンジェント)の「3倍角の公式」は、大学入試では出題頻度がそこまで高くないので別の記事にまとめます。
sin(サイン)「3倍角の公式」の覚え方

まずは、① sin「3倍角の公式」の覚え方から。
$\sin3\alpha = 3\sin \alpha – 4\sin^3 \alpha$
サンシャイン ひいて 夜風が 身にしみる
「サン(3)シャイン(sin) ひいて(−) 夜(4)風が 身(3)にし(sin)みる」
と覚えましょう。
「サンシャイン(太陽)が退(ひ)いて夜になると、冷たい風が吹いて体に染みるな〜」
というイメージで、何度も口ずさみましょう♪
cos(コサイン)「3倍角の公式」の覚え方
続いて、② cos「3倍角の公式」の覚え方は、
sin「3倍角の公式」の
- sin → cos にかえる
- 符号 → 逆 にする
と覚えておけばOK!
「3倍角の公式」の導出方法【証明】
「3倍角の公式」は、加法定理 と 2倍角の公式 から導出できます。
この2つをおさらいしたい人はこちら。
三角関数 sin cos tan「加法定理」の覚え方はないの? 加法定理の覚えやすい語呂合わせを教えてほしい! 加法定理を実際に使う問題を解きたい! こういった要望に応えます。 三角関数の「加法定理」[…]
三角関数「2倍角の公式」の覚え方を教えてほしい! 忘れてしまったときの求め方を知りたい! 「2倍角の公式」の具体的な使い方・タイミングを教えてほしい! こういった要望に応えます。 三角関数「2倍角の公[…]
sin「3倍角の公式」の導出(証明)
まずは sin「3倍角の公式」を導出してみます。
【証明】
加法定理
$ $ $\sin(\alpha + \color{red}{\beta} ) = \sin\alpha \cos\color{red}{\beta} + \cos\alpha \sin\color{red}{\beta} $
において、$\beta = 2\alpha$ とすると、
$ $ $\sin(\alpha + \color{red}{2\alpha} ) = \sin\alpha \cos \color{red}{2\alpha} + \cos\alpha \sin \color{red}{2\alpha} $
$ $ ∴ $\sin 3\alpha = \sin\alpha \color{blue}{\cos 2\alpha} + \cos\alpha \color{green}{\sin 2\alpha} $
また、2倍角の公式
$ \begin{cases}
\cos2\alpha = 1 – 2\sin^2\alpha \:・・・\color{red}{(注)} \\
\\
\sin2\alpha = 2\sin\alpha \cos\alpha \\
\end{cases} $
より、
$ $ $\sin 3\alpha = \sin\alpha \color{blue}{ \left( 1 – 2\sin^2\alpha \right) } + \cos\alpha \color{green}{ \left( 2\sin\alpha \cos\alpha \right)} $
$ $ ∴$\sin 3\alpha = \sin\alpha – 2\sin^3\alpha + 2\sin\alpha \color{red}{\cos^2 \alpha} $
ここで、
$ $ $\cos^2 \alpha = 1 – \sin^2 \alpha $
より、
$ $ ∴$\sin 3\alpha = \sin\alpha – 2\sin^3\alpha + 2\sin\alpha \color{red}{ \left( 1 – \sin^2 \alpha \right) } $
$ $ $= \sin\alpha – 2\sin^3\alpha + 2\sin\alpha – 2 \sin^3 \alpha $
$ $ $= 3 \sin\alpha – 4\sin^3\alpha $ [終]
(注)証明のゴールが「$\sin 3\alpha = 3 \sin\alpha – 4\sin^3\alpha $」なので、なるべく $\cos\alpha$ を使わず $\sin\alpha$ だけにしたい。
cos「3倍角の公式」の導出(証明)
次は cos「3倍角の公式」の導出です。流れは sin のときとほぼ同じです。
【証明】
加法定理
$ $ $\cos(\alpha + \color{red}{\beta} ) = \cos\alpha \cos \color{red}{\beta} – \sin\alpha \sin \color{red}{\beta} $
において、$\beta = 2\alpha$ とすると、
$ $ $\cos(\alpha + \color{red}{2\alpha} ) = \cos\alpha \cos \color{red}{2\alpha} – \sin\alpha \sin \color{red}{2\alpha} $
$ $ ∴$\cos 3 \alpha = \cos\alpha \color{blue}{ \cos 2\alpha} – \sin\alpha \color{green}{ \sin 2\alpha} $
また、2倍角の公式
$ \begin{cases}
\cos2\alpha = 2\cos^2\alpha – 1 \\
\\
\sin2\alpha = 2\sin\alpha \cos\alpha \\
\end{cases} $
より、
$ $ $\cos 3 \alpha = \cos\alpha \color{blue}{ \left( 2\cos^2 \alpha – 1 \right) } – \sin\alpha \color{green}{ \left( 2\sin\alpha \cos\alpha \right) } $
$ $ ∴$\cos 3 \alpha = 2\cos^3 \alpha – \cos \alpha – 2 \color{red}{\sin^2 \alpha} \cos\alpha $
ここで、
$ $ $\sin^2 \alpha = 1 – \cos^2 \alpha $
より、
$ $ $\cos 3 \alpha = 2\cos^3 \alpha – \cos \alpha – 2 \color{red}{ \left( 1 – \cos^2 \alpha \right) } \cos\alpha $
$ $ $ = 2\cos^3 \alpha – \cos \alpha – 2 \cos\alpha + 2 \cos^3 \alpha $
$ $ $ = -3\cos \alpha + 4\cos^3 \alpha$ [終]
(注)証明のゴールが「$\cos 3\alpha = – 3 \cos\alpha + 4\cos^3\alpha $」なので、なるべく $\sin\alpha$ を使わず $\cos\alpha$ だけにしたい。
「3倍角の公式」の使い方【例題】
「3倍角の公式」を使って例題を解いてみましょう。実際の入試問題の類題です。
【例題】$\displaystyle {\sin \theta = {1 \over 5} } $ $\displaystyle {\left(0<\theta<{\pi\over2} \right)}$ のとき、次の値を求めよ。 [類 11 和歌山大]
(1) $\sin 3\theta$
(2) $\cos 3\theta$
(1) $\sin 3\theta$ の値を求めよ。
$\sin3\theta = 3\sin \theta – 4\sin^3 \theta$
sin「3倍角の公式」にそのまま当てはめればOK。
【解答】
3倍角の公式より、
$\sin3\theta = 3\sin \theta – 4\sin^3 \theta$
$ $ $\displaystyle { = 3 \cdot {1 \over 5} – 4 \left( {1 \over 5} \right)^3 } $
$ $ $\displaystyle { = {3 \over 5} – {4 \over 125} } $
$ $ $\displaystyle { = {71 \over 125} } $
(2) $\cos 3\theta$ の値を求めよ。
$\cos 3\theta = -3\cos \theta + 4\cos^3 \theta$
cos「3倍角の公式」を使うために、$\cos \theta$ の値がほしいですね。
三角比の相互関係 $ \sin^2 \theta + \cos^2 \theta = 1 $ から求められそうです。
【解答】
$\cos^2 \theta = 1 – \sin^2 \theta $
$ $ $= 1 – \displaystyle { \left( { 1 \over 5 } \right)^2 } $
$ $ $= \displaystyle { 24 \over 25 } $
ここで、$\displaystyle { 0<\theta<{\pi\over2} }$ より、
$ $ $\cos\theta>0$ ・・・(注)
∴ $\displaystyle {\cos\theta = \sqrt{ 24\over 25 } }$
$ $ $= \displaystyle { 2\sqrt{6}\over 5 } $
よって、3倍角の公式より、
$\cos\theta = -3\cos \theta + 4\cos^3 \theta$
$ $ $\displaystyle { = -3 \cdot { 2\sqrt{6}\over 5 } + 4 \left( { 2\sqrt{6}\over 5 } \right) ^3 } $
$ $ $\displaystyle { = − { 6\sqrt{6}\over 5 } + { 192\sqrt{6}\over 125 } } $
$ $ $\displaystyle { = { 42\sqrt{6}\over 125 } } $
(注)$\displaystyle {0<\theta<{\pi\over2}}$ より、$\cos\theta$ の符号を 単位円で確認すると
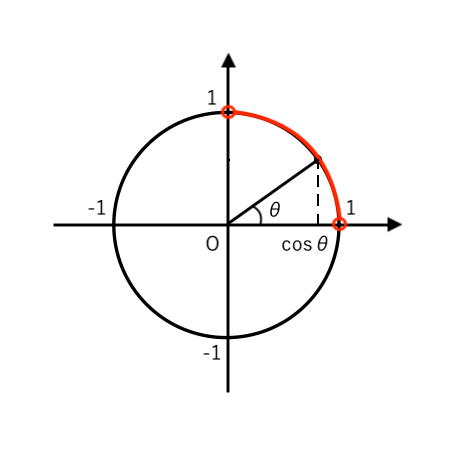
なので、$\cos\theta>0$ とわかります。
$\cos^2\theta$ の2乗を外すときに「正(プラス)の平方根」だけOKということですね。
【まとめ】三角関数「3倍角の公式」
- $\sin 3\alpha = 3\sin \alpha – 4\sin^3 \alpha$
- $\cos 3\alpha = -3\cos \alpha + 4\cos^3 \alpha$
「3倍角の公式」の覚え方は、
① 「サン(3)シャイン(sin) ひいて(−)夜(4)風が 身(3)にし(sin)みる」
② ①の sin を cos に変えて、符号を 逆 にする
バッチリ覚えておきましょう!
質問・要望があれば気軽にコメントください👍
参考:「三角比の相互関係」の公式
「三角比の相互関係」の公式をおさらいしたい人はこちら。
「三角比の相互関係」の3つの公式が覚えられない! 簡単に暗記したり、証明する方法を知りたい! 「三角比の相互関係」をいつ使うのか、タイミングや問題を教えてほしい! こういった要望に応えます。 「三角比[…]
【入試問題】「3倍角の公式」の利用
「3倍角の公式」を利用して解く 入試問題 にもっと挑戦したい人はこちら。
準備中