【中3数学】平方根（ルート○○）の大小関係の求め方【テストによく出る基本＆応用問題つき】

平方根√（ルート）の大小関係の求め方がイマイチ分からない

解き方を分かりやすく教えてほしい！

テストや入試によく出る基本問題、応用問題を解いておきたい！

こういった要望に応えます。

このページを読めば、例えば、

のような「平方根（ルート○○）の大小関係」の問題がスラスラ解けるようになります。

平方根（ルート○○）の大小関係の求め方

平方根（ルート○○）の大小関係の求め方 のポイントは

$ $　平方根を2乗する！

ということです。

平方根 は「2乗しても大小関係が変わらない」という性質があります。

この性質を利用して、平方根の大小を考えましょう。

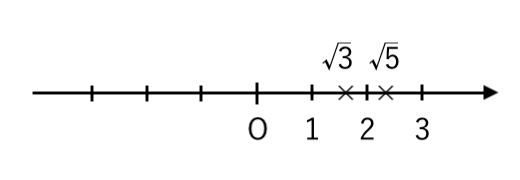
【例題1】$\sqrt{3}$ と $\sqrt{5}$ の大小を、不等号を使って表しなさい。

$ $　$\sqrt{3}$　 $\sqrt{5}$

$ $　 ↓　   ↓ 　2乗

$ $　$\sqrt{3}^\color{red}{2} $　$\sqrt{5}^\color{red}{2} $

$ $　 ||　　  ||

$ $　 $3$    $＜$    $5$

よって　$\sqrt{3}＜\sqrt{5}$

【例題2】$−\sqrt{3}$ と $−\sqrt{5}$ の大小を、不等号を使って表しなさい。

マイナスの平方根は注意！

2乗するときに「√（ルート）の部分だけ2乗」しましょう。

$ $　$−\sqrt{3}$　$−\sqrt{5}$

$ $　 ↓　　  ↓ 　ルートだけ 2乗

$ $　$−\sqrt{3}^\color{red}{2} $　$−\sqrt{5}^\color{red}{2} $

$ $　  ||　　　||

$ $　 $−3$    $＞$    $−5$

よって　$−\sqrt{3} ＞ −\sqrt{5}$

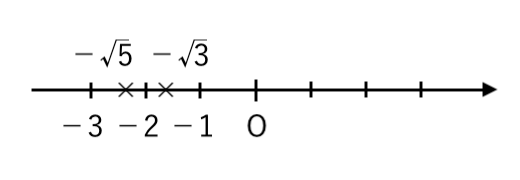
さて、ここで【例題1】の結果と見比べてみましょう。

符号がマイナスになると、大小が逆になっていますね。

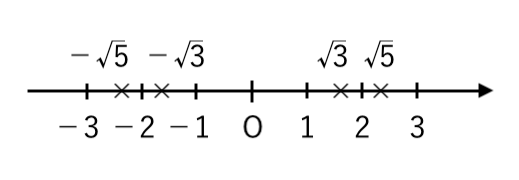
マイナスの平方根も、テストによく出るのでしっかり覚えておきましょう。

【例題3】$2$ と $\sqrt{5}$ の大小を、不等号を使って表しなさい。

整数と平方根の大小でもやり方は同じ。

$ $　$2$　 $\sqrt{5}$

$ $　↓　  ↓ 　2乗

$ $　$2^\color{red}{2} $　$\sqrt{5}^\color{red}{2} $

$ $　 ||　　||

$ $　 $4$    $＜$    $5$

よって　$2＜\sqrt{5}$

ここまでちゃんと理解できたら、次に進みましょう！

平方根（ルート○○）の大小関係【基本問題】

さっそく 平方根（ルート○○）の大小関係の問題 を解いていきましょう。

まずは基本問題からスタート！

【問題1】$ \displaystyle{ {7 \over 2}, \enspace \sqrt{11}, \enspace 2 \sqrt{3} } $ を小さい方から順に並べなさい。

【解答・解説】を見る

【解答】$ \displaystyle{ \sqrt{11}, \enspace 2 \sqrt{3}, \enspace {7 \over 2} } $

【解説】

$ $   $ \displaystyle{7 \over 2}$　　  $ \displaystyle{\sqrt{11}}$　　  $ \displaystyle{2 \sqrt{3} }$

$ $   ↓　　     ↓　 　    ↓　2乗

$ \displaystyle{ \left( {7 \over 2} \right)^2 } $　$ \displaystyle{ \left( \sqrt{11} \right)^2 }$　$ \displaystyle{ \left( { 2 \sqrt{3} } \right)^2 }$

$ $   ||　　　   ||　　　   ||

$ $  $ \displaystyle{ {49 \over 4} } $　　    $ ① \displaystyle{ 11 }$　　    $ ② \displaystyle{ 12 }$

$ $   ||　帯分数

$ $ $ ③ \displaystyle{ 12{1 \over 4} } $

※ 小さい方から①〜③をつけた

【問題2】$ \displaystyle{ { 5 \over \sqrt{3} }, { \sqrt{5} \over 3 }, { 3 \over \sqrt{5} }, { \sqrt{3} \over 5 } } $ の大小を、不等号を使って表しなさい。

【解答・解説】を見る

【解答】$ \displaystyle{ { \sqrt{3} \over 5 }＜{ \sqrt{5} \over 3 }＜{ 3 \over \sqrt{5} }＜{ 5 \over \sqrt{3} } } $

【解説】

$ $    $ \displaystyle{ 5 \over \sqrt{3} }$　　  $ \displaystyle{ \sqrt{5} \over 3 }$　　  $ \displaystyle{ 3 \over \sqrt{5} }$　　  $ \displaystyle{ \sqrt{3} \over 5 } $

$ $    ↓　　　 ↓　　 　↓　　　 ↓　2乗

$ \displaystyle{ \left( { 5 \over \sqrt{3} } \right)^2 \enspace \left( { \sqrt{5} \over 3 } \right)^2 \enspace \left( { 3 \over \sqrt{5} } \right)^2 \enspace \left( { \sqrt{3} \over 5 } \right)^2 } $

$ $　||　　　   ||　　　   ||　　　   ||

$ $   $ \displaystyle{ 25 \over 3 }$　　　$ \displaystyle{ 5 \over 9 }$　　　 $ \displaystyle{ 9 \over 5 }$　　　 $ \displaystyle{ 3 \over 25 } $

$ $　||　　　   ||　　　   ||　　　   ||　帯分数

$ $   $ ④ \displaystyle{ 8{1 \over 3 }}$　　 $ \displaystyle{ 5 \over 9 }$　　    $ ③ \displaystyle{1{ 4 \over 5 }}$　　   $ \displaystyle{ 3 \over 25 } $

$ $　  　　　    ||　　　     　　　    ||　通分

$ $　　　　  $ ② \displaystyle{ 125 \over 225 }$　　　　　  $ ① \displaystyle{ 27 \over 225 } $

※ 小さい方から①〜④をつけた

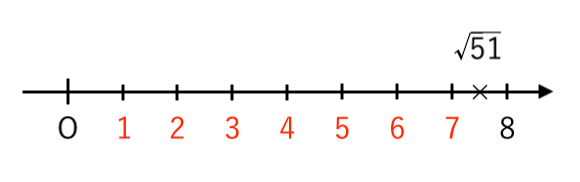
【問題3】$ \sqrt{51} $ より小さい自然数の個数を求めなさい。

【解答・解説】を見る

【解答】$7$ 個

【解説】

$ 49＜51＜64 $ より

$ \sqrt{49}＜\sqrt{51}＜\sqrt{64} $

$ 7＜\sqrt{51}＜8 $

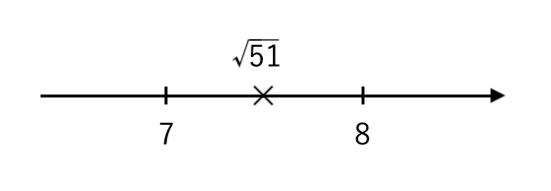
$\sqrt{51}$ より小さい自然数は

$1$〜$7$ の $7$ 個

【問題4】$ n ＜ \sqrt{130} $ をみたす自然数 $n$ のうち最も大きい自然数 $n$ の値を求めなさい。

【解答・解説】を見る

【解答】$n=12$

【解説】

$ $　$ n ＜ \sqrt{130} $

の両辺を2乗して

$ $　$ n^2 ＜ \sqrt{130}^2 $

$ $　$ n^2 ＜ 130 $

これをみたす自然数 $n$ を考えると

$ $　$1^2 = 1$　○

$ $　$2^2 = 4$　○

$ $　・

$ $　・

$ $　・

$ $　$\color{red}{11}^2 = 121$　○

$ $　$12^2 = 144$　×

よって、$n=11$ が最大

 

【別解】（問題3 と同様のやり方）

$ 121＜130＜144 $ より

$ \sqrt{121}＜\sqrt{130}＜\sqrt{144} $

$ 11＜\sqrt{130}＜12 $

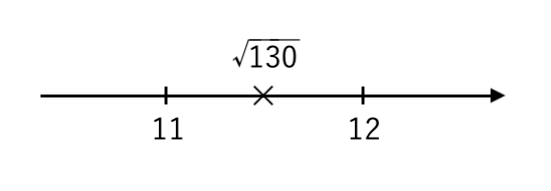
$ n ＜ \sqrt{130} $ の範囲を数直線で表すと

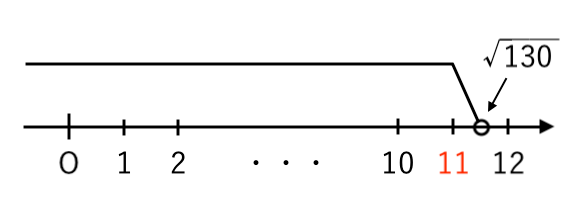
これをみたす自然数 $n$ のうち最大のものは

$ $　$n= 11$

【問題5】$ 3 ＜ \sqrt{n} ＜ 4 $ をみたす自然数 $n$ は全部で何個あるか答えなさい。

【解答・解説】を見る

【解答】$ 6 $ 個

【解説】

$ $　$ 3 ＜ \sqrt{n} ＜ 4 $

それぞれの辺を2乗して

$ $　$ 3^2 ＜ \sqrt{n}^2 ＜ 4^2 $

$ $　$ 9 ＜ n ＜ 16 $

これをみたす自然数 $n$ は

$ $　$10$ 〜 $15$

その個数は

$ $　$ 15 − 10 + 1 = 6 $（個）

 

（注）整数 $A$〜$B$ までの個数は
「$ B− A + 1 $（個）」

おしり − 頭 + 1（個）

と覚える！

【問題6】$ \displaystyle{ {7 \over 3} ＜ n ＜ \sqrt{29} } $ をみたす自然数 $n$ をすべて求めなさい。

【解答・解説】を見る

【解答】$n=3, \enspace 4,\enspace 5$

【解説】

$ $　$ \displaystyle{ {7 \over 3} ＜ n ＜ \sqrt{29} } $

それぞれの辺を2乗して

$ $　$ \displaystyle{ \left( {7 \over 3} \right)^2 ＜ n^2 ＜ \sqrt{29}^2 } $

$ $　$ \displaystyle{ {49 \over 9} ＜ n^2 ＜ 29 } $

$ $　$ \displaystyle{ 5{4 \over 9} ＜ n^2 ＜ 29 } $

これをみたす自然数 $n$ を考えると

$ $　$n= 3$ のとき　$n^2=3^2 = 9$　○

$ $　$n= 4$ のとき　$n^2=4^2 = 16$　○

$ $　$n= 5$ のとき　$n^2=5^2 = 25$　○

以上、基本問題でした。

ここまでの問題パターンをマスターしておけば、学校の定期テストはひとまず安心です。

平方根（ルート○○）の大小関係【応用問題】

続いて、平方根（ルート○○）の大小関係の応用問題 を解いていきましょう。

2乗すると手詰まりになってしまうパターンの問題です。

このパターンは「数直線をかく」やり方が効きます。

【問題1】$ −3 \sqrt{3} ＜a≦−1 $ をみたす整数 $a$ は全部で何個あるか答えなさい。

【解答・解説】を見る

【解答】$5$ 個

【解説】

$ −3 \sqrt{3} ＜a≦−1 $ より

$ − \sqrt{27} ＜a≦−1 $

 

ここで

$ 25＜ 27 ＜36 $ より

$ \sqrt{25}＜ \sqrt{27} ＜ \sqrt{36} $

$ 5＜ \sqrt{27} ＜6 $

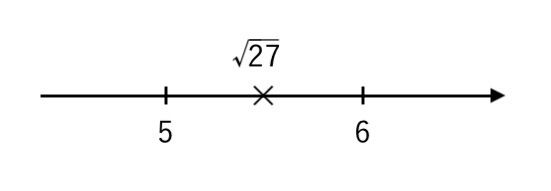
符号をマイナスにすると、大小が逆になるので

$ −5 \color{red}{＞} − \sqrt{27} \color{red}{＞} −6 $

つまり

$ −6＜ − \sqrt{27} ＜−5 $

 

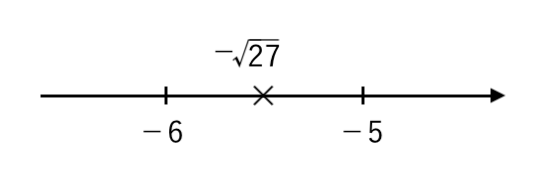
よって、$ − \sqrt{27} ＜a≦−1 $ をみたす整数 $a$ は

$ $　$−5$ 〜 $−1$

（注）$−1$ を含む

その個数は

$ $　$(−1)−(−5)+1 = 5$（個）

【問題2】$ −2.9 ＜ n ＜ \sqrt{21} $ をみたす整数 $n$ は全部で何個あるか答えなさい。

【解答・解説】を見る

【解答】 $ 7 $ 個

【解説】

$ 16＜ 21 ＜25 $ より

$ \sqrt{16}＜ \sqrt{21} ＜ \sqrt{25} $

$ 4＜ \sqrt{21} ＜5 $

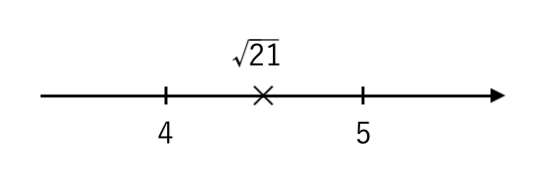
よって、$ −2.9 ＜ n ＜ \sqrt{21} $ をみたす整数 $n$ は

$ $　$−2$ 〜 $4$

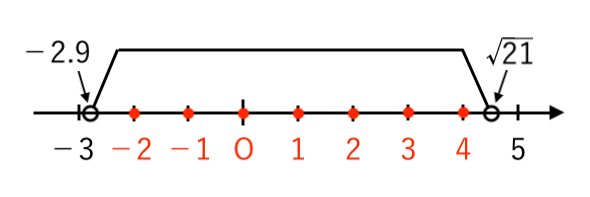
その個数は

$ $　$ 4 − (−2) + 1 = 7 $（個）

【問題3】$ a−1 ＜ \sqrt{34} ＜ a+3 $ をみたす自然数 $a$ は全部で何個あるか答えなさい。

【解答・解説】を見る

【解答】$4$ 個

【解説】

$ 25＜ 34 ＜36 $ より

$ \sqrt{25}＜ \sqrt{34} ＜ \sqrt{36} $

$ 5＜ \sqrt{34} ＜6 $

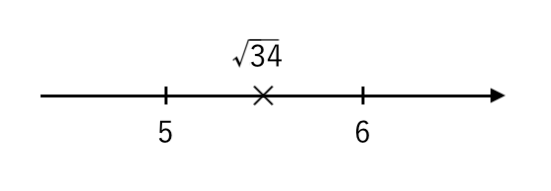
$a−1$（左端）と $ a+3$（右端）が $4$ だけ離れていることを考えると

$ $[1] $a−1=5$ のとき　$a=6$（最大）

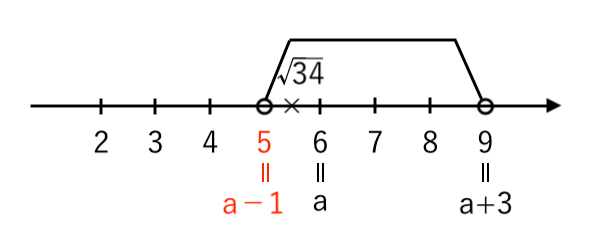
$ $[2] $a+3=6$ のとき　$a=3$（最小）

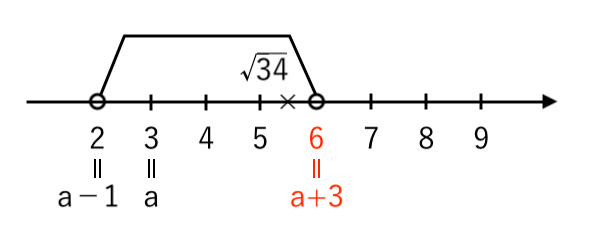
よって、条件をみたす自然数 $a$ は

$ $　$3$ 〜 $6$

その個数は

$ $　$6−3+1=4$（個）

以上です。お疲れ様でした！

【まとめ】平方根（ルート○○）の大小関係の求め方

平方根（ルート○○）の大小関係の求め方 のポイントは

$ $　平方根を2乗する！

ということ。

それでもダメなら

$ $　数直線をかく

と覚えておきましょう。

平方根（ルート○○）の整数部分、小数部分の求め方

関連記事

【中学数学】平方根（ルート○○）の整数部分、小数部分の求め方はこれだけ！【基本＆応用問題つき】

平方根√（ルート）の整数部分、小数部分の求め方がよく分からない そもそも√の数の整数部分、小数部分って何？ わかりやすく解説してほしい！ こういった疑問・要望にこたえます。   このページを読めば、中学数[…]

平方根（ルート○○）が自然数となる n の求め方

関連記事

【中3数学】「平方根（ルート○○）が自然数となるn」を簡単に求める方法【基本＆応用問題つき】

平方根の「ルート○○が自然数となるn」の求め方がよく分からない 簡単に求める方法はないの？ テストや入試によく出る問題を解いておきたい！ こういった要望に応えます。   例えば、 $ \sqrt{28n[…]

質問・要望があれば気軽にコメントください👍