平方根√(ルート)の整数部分、小数部分の求め方がよく分からない
そもそも√の数の整数部分、小数部分って何?
わかりやすく解説してほしい!
こういった疑問・要望にこたえます。
このページを読めば、中学数学における平方根の
のようなパターンの問題を迷うことなくスラスラ解けるようになります。
- 1 平方根(ルート○○)の整数部分・小数部分【基本編】
- 2 平方根(ルート○○) の整数部分、小数部分を求める問題【基本編】
- 3 a√b の整数部分・小数部分の求め方【応用編】
- 4 −√a の整数部分・小数部分の求め方【応用編】
- 5 平方根(ルート○○) の整数部分、小数部分を求める問題【応用編】
- 5.1 【問題1】$ 2 \sqrt{5} − 2 $ の小数部分を $a$ とするとき、$ a^2+4a $ の値を求めなさい。
- 5.2 【問題2】$ 5 − \sqrt{2} $ の整数部分を $a$ 、小数部分を $b$ とするとき、$ \displaystyle{ b^2 + {1 \over 3} ab } $ の値を求めなさい。
- 5.3 【問題3】$ \left( \sqrt{2} + \sqrt{3} \right)^2 $ の小数部分を $x$ とするとき、$ x^2 + 8x −20 $ の値を求めなさい。
- 5.4 【問題4】$ \sqrt{n} $ の整数部分が $3$ となるような自然数 $n$ の値は何個あるか答えなさい。
- 6 最後に
- 7 「平方根(ルート○○)が自然数となるn」の求め方
- 8 平方根(ルート○○)の大小関係の求め方
平方根(ルート○○)の整数部分・小数部分【基本編】
まずは「平方根√(ルート)の数の整数部分・小数部分って何?」から解説します。
【例題1-1】$ \sqrt{7}$ の整数部分、小数部分を求めなさい。
もし $ \sqrt{7} = \color{red}{2}.\color{blue}{645 ⋯ } $ という近似値(きんじち)を覚えていれば、
・整数部分は $ \color{red}{2}$
・小数部分は $ \sqrt{7} − \color{red}{2}$
($ = \color{red}{2}.\color{blue}{645 ⋯ } − \color{red}{2} = 0. \color{blue}{645 ⋯ } $)
であっさり終わりです。
ですが、例えば $ \sqrt{19} $ とかになると、ほとんどの人は覚えてないですよね?
なので、次のやり方をマスターしておきましょう。
まず「$ \sqrt{7}$」を2乗した形「$7$」で考えます。
$○^2<7<□^2$ となるような数ではさむと
$○<\sqrt{7}<□$ と分かりますね。
$4<7<9$ より
$ \sqrt{4}<\sqrt{7}<\sqrt{9} $
$ \color{red}{2}<\sqrt{7}<3 $
$ \sqrt{7}$ が $2$ と $3$ の間にあることが分かりました。
これを 数直線で表す と
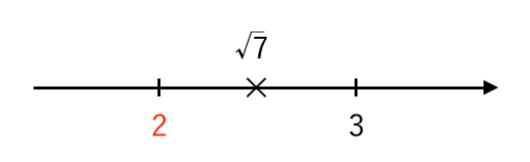
こんな感じなので、
$ $ $ \sqrt{7} = \color{red}{2} . \color{blue}{⋯} $
というところまでは言えますね。
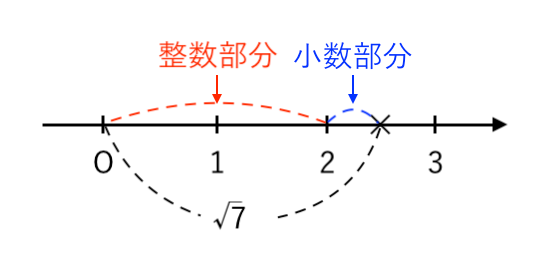
整数部分は、$\sqrt{7} $ を超えない最大の整数の「$\color{red}{2}$」です。
小数部分は、$\sqrt{7} $ から 整数部分の $\color{red}{2}$ を引いたものなので「$ \color{blue}{\sqrt{7} − 2} $」です。
よって、$ \sqrt{7} $ の
・整数部分は $\color{red}{2}$
・小数部分は $ \color{blue}{\sqrt{7} − 2} $
小数部分の求め方は、次のように覚えておきましょう。
【例題1-2】$ \sqrt{10}$ の整数部分、小数部分を求めなさい。
さっきと同じように考えてみます。
$9<10<16$ より
$ \sqrt{9}<\sqrt{10}<\sqrt{16} $
$ \color{red}{3}<\sqrt{10}<4 $
数直線で表すと
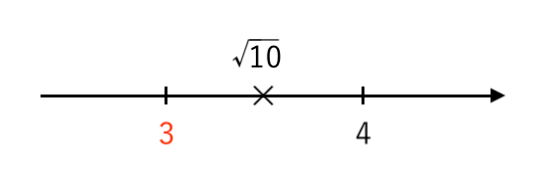
よって、$\sqrt{10}$ の
・整数部分は $\color{red}{3}$
・小数部分は $\sqrt{10}−3 $
ここまで理解できたら次に進みましょう。
平方根(ルート○○) の整数部分、小数部分を求める問題【基本編】
さっそく「平方根(ルート○○)の整数部分、小数部分を求める問題」をやってみましょう!
まずは 基本問題 からスタート!
【問題1】$ \sqrt{6}$ の整数部分、小数部分を求めなさい。
- 【解答・解説】を見る
-
【解答】整数部分 $ 2 $、小数部分 $ \sqrt{6}−2 $
【解説】
$4<6<9$ より
$ \sqrt{4}<\sqrt{6}<\sqrt{9} $
$ \color{red}{2}<\sqrt{6}<3 $
数直線で表すと

よって、$\sqrt{6}$ の
・整数部分は $\color{red}{2}$
・小数部分は $\sqrt{6}−2 $
【問題2】$ 2 + \sqrt{2}$ の整数部分、小数部分を求めなさい。
まずは $ \sqrt{2} $ の整数部分を求めるところからスタートしましょう。
- 【解答・解説】を見る
-
【解答】整数部分 $ 3 $、小数部分 $ \sqrt{2}−1 $
【解説】
$1<2<4$ より
$ \sqrt{1}<\sqrt{2}<\sqrt{4} $
$ 1<\sqrt{2}<2 $
それぞれの辺に $2$ を足して
$ 1+2<2+ \sqrt{2}<2+2 $
$ \color{red}{3}<2+ \sqrt{2}<4 $
数直線で表すと
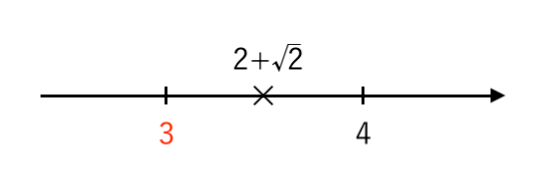
よって、$ 2+ \sqrt{2}$ の
・整数部分は $\color{red}{3}$
・小数部分は $ \left( 2+ \sqrt{2} \right)−3 = \sqrt{2} −1 $
【問題3】$ \sqrt{5} $ の小数部分を $a$ とするとき、$ a^2 + a −2$ の値を求めなさい。
$ \sqrt{5} $ の小数部分を求めてから、$ a^2 + a −2 $ にそのまま代入すると計算が少し大変ですね。
- 【解答・解説】を見る
-
【解答】$ 5−3 \sqrt{5} $
【解説】
$4<5<9$ より
$ \sqrt{4}<\sqrt{5}<\sqrt{9} $
∴ $ \color{red}{2}<\sqrt{5}<3 $
数直線で表すと
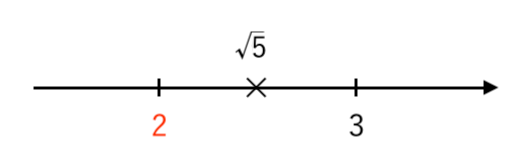
よって、$\sqrt{5}$ の
・整数部分は $ \color{red}{2} $
・小数部分は $ a= \sqrt{5}−2 $
ゆえに
$ a^2 +a −2$
$ = (a−1)(a+2)$ (因数分解)
$ = \left(\sqrt{5}−2−1 \right) \left(\sqrt{5}−2 + 2 \right) $ ($a$ を代入)
$ = \left(\sqrt{5}−3 \right) \sqrt{5} $
$ = 5−3 \sqrt{5} $
以上、基本編でした!
a√b の整数部分・小数部分の求め方【応用編】
ここからは、中学数学の「平方根の応用」に入ります。
まずは、a√b の整数部分・小数部分 の求め方です。
【例題2-1】$ 2 \sqrt{5}$ の整数部分、小数部分を求めなさい。
これは要注意! まずはよくあるダメな例から。
×【NG例】
$4<5<9$ より
$ $ $ \sqrt{4}<\sqrt{5}<\sqrt{9} $
$ $ $ 2<\sqrt{5}<3 $
それぞれの辺に $2$ をかけて
$ $ $ 4<2 \sqrt{5}<6 $
数直線で表すと
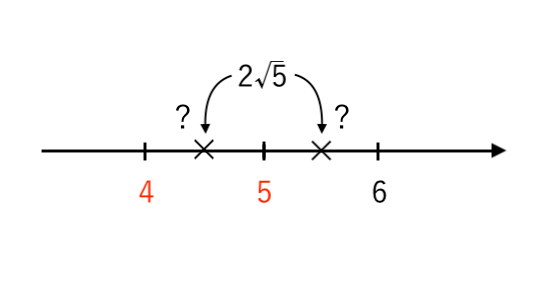
整数部分は・・・?
「あれ?整数部分って $4$ と $5$ のどっちだ?」となってしまい、うまくいきません。
というわけで、正しいやり方はこちら。
◎【OK例】
$ 2 \sqrt{5} = \sqrt{20} $
$16<20<25$より
$ $ $ \sqrt{16}<\sqrt{20}<\sqrt{25} $
$ $ $ 4<\sqrt{20}<5 $
$ $ $ \color{red}{4}<2 \sqrt{5}<5 $
数直線で表すと
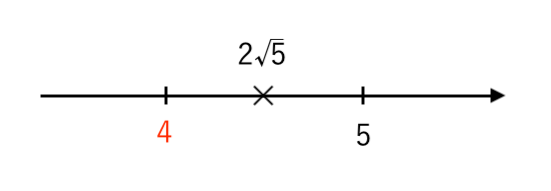
よって
・整数部分は $\color{red}{4}$
・小数部分は $ 2 \sqrt{5}−4 $
となり、正しく求められました。
a√b の整数部分・小数部分 の求め方をまとめると
−√a の整数部分・小数部分の求め方【応用編】
続いて、−√a の整数部分・小数部分 の求め方です。
【例題3-1】$ 5−\sqrt{6}$ の整数部分、小数部分を求めなさい。
まずは「$ \sqrt{6} $ がどんな値か?」から考えます。
【解答】
$4<6<9$ より
$ $ $ \sqrt{4}<\sqrt{6}<\sqrt{9} $
$ $ $ 2<\sqrt{6}<3 $
それぞれの辺に $−1$ をかけて
$ $ $ −2>− \sqrt{6}>−3 $ ・・・(注)
$ $ $ −3<− \sqrt{6}<−2 $
それぞれの辺に $5$ を足して
$ $ $ −3+5<5− \sqrt{6}<−2+5 $
$ $ $ \color{red}{2}<5 − \sqrt{6}<3 $
数直線で表すと
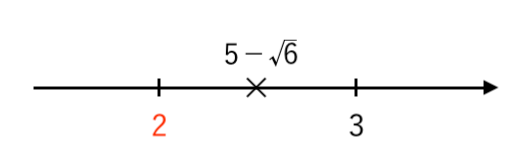
よって
・整数部分は $\color{red}{2}$
・小数部分は $ \left( 5 − \sqrt{6} \right)−2 = 3 − \sqrt{6} $
(注)不等式にマイナスの数をかけると、不等号の向きが逆になる(大小関係が逆になるってこと)
−√a の整数部分・小数部分 の求め方をまとめると
平方根(ルート○○) の整数部分、小数部分を求める問題【応用編】
それでは「平方根(ルート○○)の整数部分、小数部分を求める問題」(応用問題)にチャレンジしてみましょう!
【問題1】$ 2 \sqrt{5} − 2 $ の小数部分を $a$ とするとき、$ a^2+4a $ の値を求めなさい。
- 【解答・解説】を見る
-
【解答】$ 20 −8 \sqrt{5} $
【解説】
$ 2 \sqrt{5} = \sqrt{20} $
$16<20<25$より
$ $ $ \sqrt{16}<\sqrt{20}<\sqrt{25} $
$ $ $ 4<\sqrt{20}<5 $
$ $ $ 4<2 \sqrt{5}<5 $
それぞれの辺から $2$ を引いて
$ $ $ \color{red}{2}<2 \sqrt{5} −2 <3 $
数直線で表すと
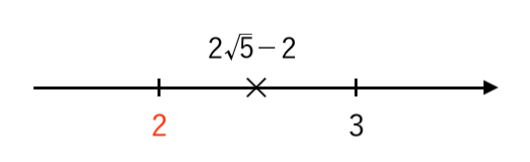
よって、$ 2 \sqrt{5} −2 $ の
・整数部分は $\color{red}{2}$
・小数部分は $ a = \left( 2 \sqrt{5} −2 \right) −\color{red}{2} = 2 \sqrt{5}−4 $
ゆえに
$ a^2 +4a $
$ = a(a+4) $(因数分解)
$ = \left( 2 \sqrt{5}−4 \right) \left( 2 \sqrt{5}−4 + 4 \right) $($a$ を代入)
$ = \left( 2 \sqrt{5}−4 \right) × 2 \sqrt{5} $
$ = 20 −8 \sqrt{5} $
【問題2】$ 5 − \sqrt{2} $ の整数部分を $a$ 、小数部分を $b$ とするとき、$ \displaystyle{ b^2 + {1 \over 3} ab } $ の値を求めなさい。
- 【解答・解説】を見る
-
【解答】$ 8 − 5 \sqrt{2} $
【解説】
$1<2<4$ より
$ $ $ \sqrt{1}<\sqrt{2}<\sqrt{4} $
$ $ $ 1<\sqrt{2}<2 $
それぞれの辺に $−1$ をかけて
$ $ $ −1>− \sqrt{2}>−2 $ ←【例題3-1】参照
$ $ $ −2< − \sqrt{2}<−1 $(左右を逆にした)
それぞれの辺に $5$ を足して
$ $ $ \color{red}{3}< 5 − \sqrt{2}<4 $
数直線で表すと
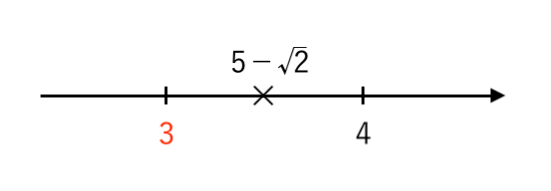
よって、$ 5 − \sqrt{2} $ の
・整数部分は $ a = \color{red}{3}$
・小数部分は $ b = \left( 5 − \sqrt{2} \right) −\color{red}{3} = 2 − \sqrt{2} $
ゆえに
$ \displaystyle{ b^2 + {1 \over 3} ab } $
$ \displaystyle{ = b \left( b + {1 \over 3} a \right) } $
$ \displaystyle{ = \left( 2 − \sqrt{2} \right) \left( 2 − \sqrt{2} + {1 \over \require{cancel} \bcancel{3} } × \bcancel{3} \right) } $($a, b$ を代入)
$ \displaystyle{ = \left( 2 − \sqrt{2} \right) \left( 3 − \sqrt{2} \right) } $
$ \displaystyle{ = 6 − 5 \sqrt{2} + 2 } $
$ \displaystyle{ = 8 − 5 \sqrt{2} } $
【問題3】$ \left( \sqrt{2} + \sqrt{3} \right)^2 $ の小数部分を $x$ とするとき、$ x^2 + 8x −20 $ の値を求めなさい。
まずは $ \left( \sqrt{2} + \sqrt{3} \right)^2 $ を展開してみましょう。
- 【解答・解説】を見る
-
【解答】$ −12 $
【解説】
$ \left( \sqrt{2} + \sqrt{3} \right)^2 $
$ = 2 + 2 \sqrt{6} + 3 $
$ = 5 + 2 \sqrt{6} $
$ = 5 + \sqrt{24} $ ←【例題2-1】参照
ここで
$ $ $16<24<25$
$ $ $ \sqrt{16} < \sqrt{24} < \sqrt{25} $
$ $ $ 4 < \sqrt{24} < 5 $
$ $ $ 4 < 2 \sqrt{6} < 5 $
それぞれの辺に $5$ を足して
$ $ $ \color{red}{9} < 5 + 2 \sqrt{6} < 10 $
数直線で表すと
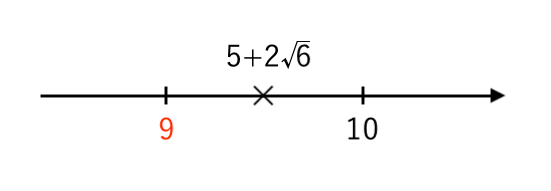
よって、$ 5 + 2 \sqrt{6} $ の
・整数部分は $ \color{red}{9}$
・小数部分は $ x = \left( 5 + 2 \sqrt{6} \right) −\color{red}{9} = 2 \sqrt{6} −4 $
ゆえに
$ x^2 + 8x −20 $
$ = (x + 10) (x −2) $
$ = \left( 2 \sqrt{6} −4 + 10 \right) \left( 2 \sqrt{6} −4 −2 \right) $($x$ を代入)
$ = \left( 2 \sqrt{6} + 6 \right) \left( 2 \sqrt{6} −6 \right) $
$ = \left( 2 \sqrt{6} \right)^2 −6^2 $ ← 展開の公式 $ (x+y)(x−y) = x^2 − y^2 $ を利用
$ = 24 −36 $
$ = −12 $
【問題4】$ \sqrt{n} $ の整数部分が $3$ となるような自然数 $n$ の値は何個あるか答えなさい。
いよいよラストです。
もし整数部分で困ったら、とりあえず数直線をかいて考えましょう。
- 【解答・解説】を見る
-
【解答】$ 7 $ 個
【解説】
$ \sqrt{n} $ の整数部分が $3$ なので
$ $ $ \color{red}{3} ≦ \sqrt{n} < 4 $
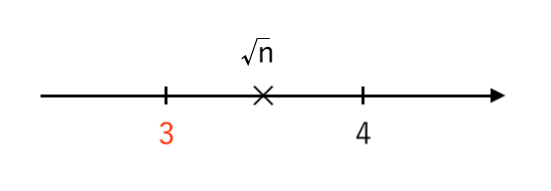
つまり
$ $ $ \sqrt{9} ≦ \sqrt{n} < \sqrt{16} $
ルートの中身だけ見ると
$ $ $ 9 ≦ n < 16 $
これを満たす $n$ の値は
$ $ $ n = 9, 10, 11, … 15 $
よって、その個数は
$ $ $ 15 − 9 + 1 = 7 $(個)
(注)整数 $A$〜$B$ までの個数は
「$ B− A + 1 $(個)」おしり − 頭 + 1(個)
と覚える!
最後に
最後にまとめです。
「平方根(ルート○○)の整数部分、小数部分を求める問題」を解くときは
$ $ 数直線をかく
のがオススメ!
「平方根(ルート○○)が自然数となるn」の求め方
のようなパターンの問題の解き方をマスターしたい人はこちら。
平方根の「ルート○○が自然数となるn」の求め方がよく分からない 簡単に求める方法はないの? テストや入試によく出る問題を解いておきたい! こういった要望に応えます。 例えば、 $ \sqrt{28n[…]
平方根(ルート○○)の大小関係の求め方
平方根√(ルート)の大小関係の求め方がイマイチ分からない 解き方を分かりやすく教えてほしい! テストや入試によく出る基本問題、応用問題を解いておきたい! こういった要望に応えます。 このページを読めば[…]
質問・要望があれば気軽にコメントください👍


