2次方程式の利用(文章問題)をどうやって解いたらいいのか分からない・・・
自然数とか図形の文章題がニガテでうまく解けないよ〜!
テスト・高校入試によくでるパターンの問題をやっておきたい!
こんなお悩みを解決します。
このページを読めば、「2次方程式の利用(文章問題)」で テストや高校入試でよくでるパターンの問題 をマスターできます。
自然数や図形がからんでくる文章題を、しっかり解けるように練習しておきましょう!
【中3数学】2次方程式の利用(文章問題)のポイント

「2次方程式の利用(文章問題)」の解き方の手順は
- 求めたい数を文字($x$など)でおく
- 文章を読んで方程式を立てる
- 方程式を解く
- 答えを書く
この4ステップでやるとスムーズに解けます。
具体的なやり方は、実際の問題で解説していきます!
【中3数学】2次方程式の利用(文章問題)の解き方【自然数パターン】
まずは「自然数」について2次方程式を立てて解くパターンの例題を解いてみましょう。
例えば、こんな問題。
【例題1】大小2つの自然数がある。大きい方の数は、小さい方の数より $9$ 大きい。
また、小さい方の数を $2$乗してから $3$をひくと、大きい方の数に等しくなる。
このとき、これらの2つの自然数を求めなさい。
①求めたい数を文字でおく
求めたい数は「大小2つの自然数」です。
小さい方の数を「$\color{blue}{x} $」とおくと、大きい方の数はそれより $9$ 大きいので「$ \color{red}{x+9} $」とおけます。
②文章を読んで方程式を立てる
小「$ \color{blue}{x} $」、大「$ \color{red}{x+9} $」の2つの数を問題文に当てはめていきましょう。
これを方程式(等式)になおすと
$ $ $ \color{blue}{x}^2 -3 = \color{red}{x+9} $
になります。
③方程式を解く
②で立てた方程式を解きます。
$ $ $ x^2 -3 = x+9 $
$ $ $ x^2 -x -12 = 0 $
$ $ $ (x – 4)(x+3) = 0$
$ $ $ x = -3, \enspace 4$
④答えを書く
そんなの当たり前じゃないか!と思ったかもしれませんが、ここで大切なのは
「問題に合った答え」を書くということです。
今回は「大小2つの自然数」を答える必要があります。
③で求めた解 $ x = -3, 4$ のうち、自然数なのは $x=4$ だけ。
小さい方の数($x$)が $4$ なので
大きい方の数($x+9$)は $4+9 = 13$
よって
このような手順で解くと、スムーズに答えにたどり着きます。
【中3数学】2次方程式の利用(文章問題)の解き方【図形パターン】
もう1つ例題をやっておきましょう。
今度は「図形」について2次方程式を立てて解くパターンです。
【例題2】
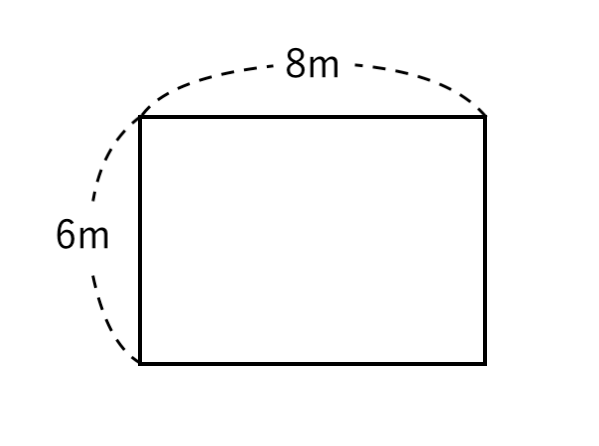
上図のように、縦の長さ $6 m $、横の長さ $8 m $ の長方形の形をした花だんがある。
縦、横をそれぞれ同じ長さだけのばして、面積が最初のときより $72 m^2 $ だけ大きくなるようにしたい。
何$ m $ のばせばよいか求めなさい。
①求めたい数を文字でおく
縦、横をそれぞれ $x (m)$ のばしたとします。
②文章を読んで方程式を立てる
2次方程式に限らず、文章題では「図をかく」ということが一番のポイントです。
この問題では、縦、横をそれぞれ $x \enspace (m)$ のばすと、
縦 $6+x \enspace (m)$、横 $8+x \enspace (m)$ になります(下図)。
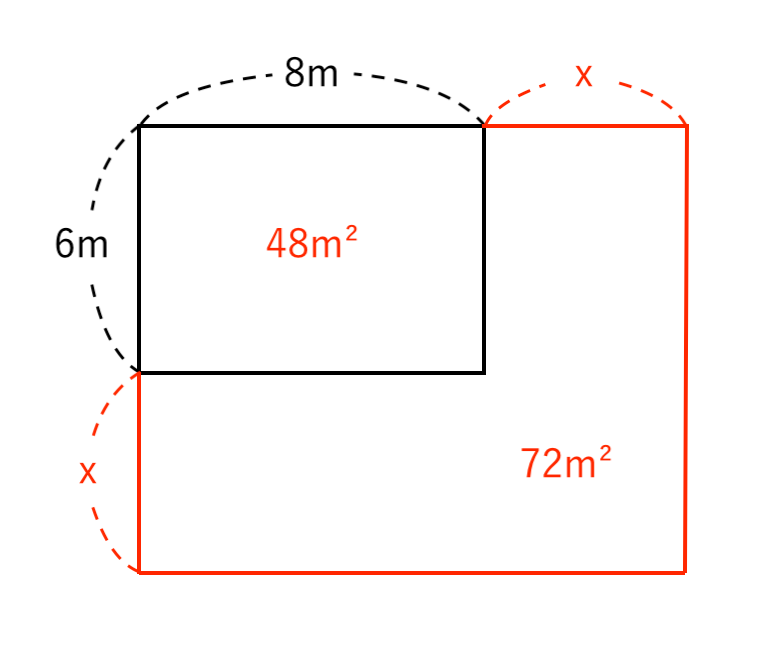
問題文の中に
とあるので、合計の面積は $48 + 72 = 120 \enspace (m^2)$ となります。
長さをのばした後の花だんの面積について、方程式を立てると
$ $ $ (6+x)(8+x) = 120$
③方程式を解く
②の方程式を解くと
$ $ $ 48 + 14x + x^2 = 120$
$ $ $ x^2 + 14x -72 = 0 $
$ $ $ (x + 18)(x – 4) = 0 $
$ $ $ x= -18, \enspace 4 $
④答えを書く
$x$ は「のばした長さ」なので正の数になりますね。
よって、2次方程式の解 $ x= -18, \enspace 4 $ のうち $x = 4$ だけOK。
「何$m$ のばせばよいか?」を答えるので、
【中3数学】2次方程式の利用(文章問題)【練習問題】
ここまで学んだことを活かして「2次方程式の利用」の練習問題を解いてみましょう!
学校のテスト・高校入試で出やすいパターンの問題 を用意しました。
さっきの例題のような「自然数」「図形」パターン以外の問題も入れてあります。
問題1(自然数)
ある正の整数 $a$ を2乗してから3倍しなければならないのに、誤って3倍してから2乗したため、答えが $216$ 大きくなってしまった。
このとき、$a$ の値を求めなさい。
- 【解答・解説】を見る
-
【解答】$a = 6$
【解説】
問題文に沿って、方程式を作ります。
ある正の整数 $a$ を2乗($^2$)してから3倍($×3$)しなければならないのに、誤って3倍($×3$)してから2乗($^2$)したため、答えが $216$ 大きくなってしまった。- 正しい計算:$ a^2 × 3 = \color{blue}{3a^2} $
- 誤った計算:$ (a × 3 )^2 = (3a)^2 = \color{red}{9a^2} $
問題文より
「(誤った計算)$=$(正しい計算)$+ \enspace 216$ 」なので
$ $ $ \color{red}{9a^2} = \color{blue}{3a^2} + 216 $
$ $ $ 6a^2 = 216 $
$ $ $ a^2 = 36 $
$ $ $ a = \pm 6 $
$a$ は正の整数なので $a = 6$ が正しいですね。
問題2(自然数)
連続する3つの自然数がある。
この3つの自然数のそれぞれの平方の和が $365$ であるとき、連続する3つの自然数を求めなさい。
- 【解答・解説】を見る
-
【解答】$10, \enspace 11, \enspace 12$
【解説】
連続する3つの自然数とは、例えば $ 3, 4, 5 $ のような数ですね。
仮に真ん中の $4$ を「$x$」とおくと、
$ $ 1つ小さい $\color{blue}{3}$ は「$\color{blue}{x-1}$」
$ $ 1つ大きい $\color{red}{5}$ は「$\color{red}{x+1}$」
とおけます。
なので、連続する3つの自然数を $ \color{blue}{x-1} , \enspace x, \enspace \color{red}{x+1} $ とおくと
それぞれの平方(2乗)の和が $365$ なので、
$ $ $(\color{blue}{x-1})^2 + x^2 +(\color{red}{x+1})^2 = 365 $
$ $ $ x^2 -2x +1 + x^2 + x^2 +2x + 1 = 365 $
$ $ $ 3x^2 = 363 $
$ $ $ x^2 = 121 $
$ $ $ x = \pm 11 $
ここで、$x$ は自然数なので
$ $ $ x = 11 $ (真ん中の数)
問題3(図形)
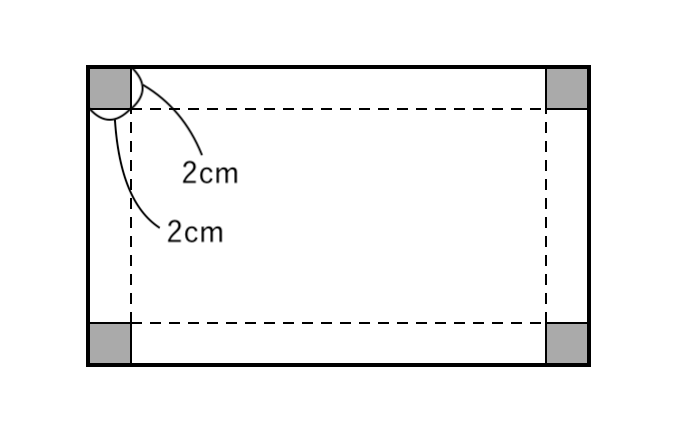
上図のように、横が縦より $10cm$ 長い長方形の厚紙がある。この4すみから 1辺が $2cm$ の正方形を切り取り、直方体の容器を作ると、容積が $150cm^3$ になった。このとき、はじめの厚紙の縦の長さを求めなさい。
- 【解答・解説】を見る
-
【解答】$9cm$
【解説】
はじめの厚紙の縦の長さを「$x \enspace (cm)$」とおくと、横の長さは「$x+10 \enspace (cm)$」になります。
そこから分かる長さは以下の通り。
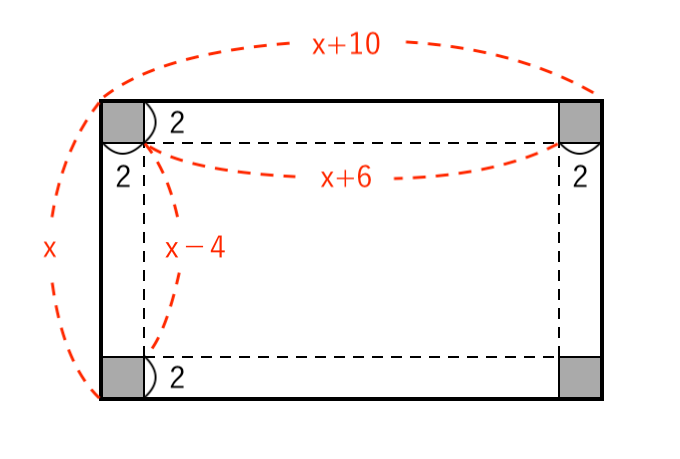
これを組み立てて、直方体を作ると
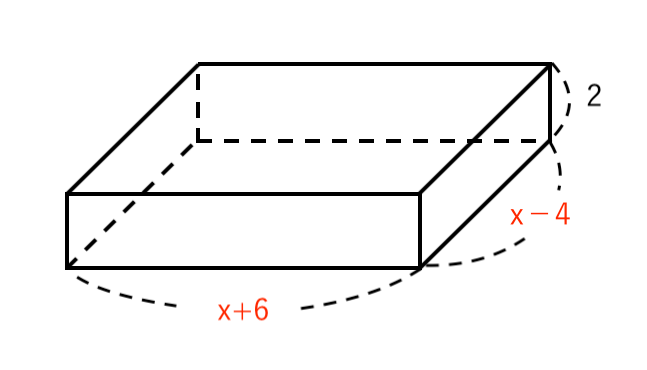
直方体の容積について 方程式を立てると
$ $ $ 2(x -4)(x+6) = 150 $
$ $ $ (x -4)(x+6) = 75 $
$ $ $ x^2 +2x -24 = 75 $
$ $ $ x^2 +2x -99 = 0 $
$ $ $ (x + 11)(x-9) = 0 $
$ $ $ x = -11, \enspace 9 $
厚紙の縦の長さ $x$ は正の数なので $x=9$
問題4(損益算)
ある商店では、品物A 1個を $500$円で仕入れている。Aの定価は、仕入れた値段に $x$% の利益を見込んでつけている。ある日のセールで、Aを定価の $x$% 引きで売ることにした。ただし、消費税は考えないものとする。
(1) Aの定価を、$x$ を使った式で表しなさい。
(2) このセールで、A 1個の売り値は $455$円だった。$x$の値を求めなさい。
- 【解答・解説】を見る
-
【解答】(1) $ 500 + 5 x $ (2) $ x = 30 $
【解説】
(1) 損益算 の問題は 線分図 をかいて「比」で考えると分かりやすいです。
問題文の
Aの定価は、仕入れた値段に $x$% の利益を見込んでつけている。から「比」を考えると
「定価 $=$ 仕入れ値 $+$ 利益」なので
$ $ 仕入れ値:利益:定価 $\displaystyle{ = 1:{x \over 100}:\color{red} { \left( 1 + {x \over 100} \right) } } $
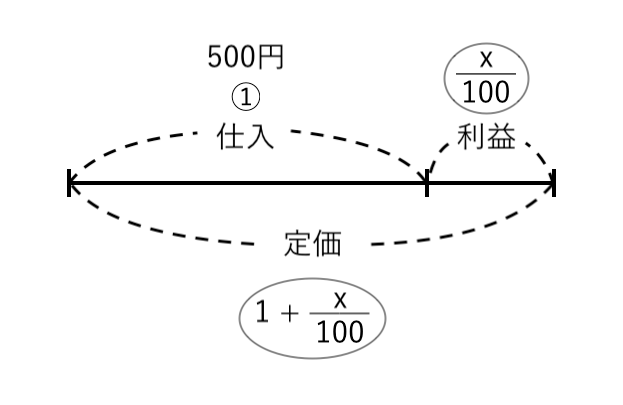
よって、定価は
$ $ $ \displaystyle{ 500 \left( 1 + { x \over 100 } \right) } $
$ $ $ = 500 + 5 x $
と表せます。
※ ここの計算は、仕入れ値:定価 の「比例式」を解いてもOK
$ $ $\displaystyle{ 500 : 定価 = 1:\left( 1 + {x \over 100} \right) } $ より
$ $ $\displaystyle{ 定価 = 500 \left( 1 + {x \over 100} \right) } $
(2) 問題文の
ある日のセールで、Aを定価の $x$% 引きで売ることにした。から「比」を考えると
「売り値 $=$ 定価 $−$ 値引き」なので
$ $ 定価:値引き:売り値 $ \displaystyle{ = 1:{x \over 100} :\color{red} { \left( 1 − {x \over 100} \right) } } $
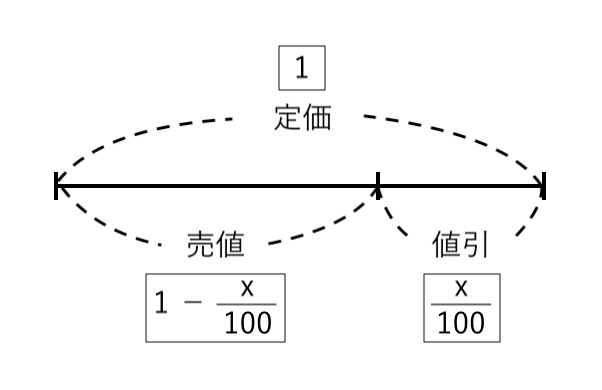
よって、売り値 について方程式を立てると
$ $ $ \color{red} { 売り値 } = 455 $
$ $ $ 定価 × \displaystyle{ \left( 1 − {x \over 100} \right) = 455 } $
$ $ $ \displaystyle{ (500 + 5 x) \left( 1 − {x \over 100} \right) = 455 } $
両辺に $100$ をかけて
$ $ $ \displaystyle{ (500 + 5 x) \left( 1 − {x \over 100} \right) ×100 = 45500 } $
$ $ $ (500 + 5 x) (100 − x) = 45500 $
$ $ $ 5 (100 + x) (100 − x) = 45500 $
両辺を $5$ で割って
$ $ $ (100 + x) (100 − x) = 9100 $
$ $ $ 10000 − x^2 = 9100 $
$ $ $ x^2 = 900 $
$ $ $ x = \pm 30 $
$x$ は正の数より $x = 30$
【まとめ】2次方程式の利用(文章問題)の解き方
最後に「2次方程式の利用(文章問題)」の解き方のおさらいです。
- 求めたい数を文字($x$など)でおく
- 文章を読んで方程式を立てる
- 方程式を解く
- 答えを書く
図形や損益算などの文章問題は「図をかく」ということを覚えておきましょう!
【2次方程式】解き方 3パターン
二次方程式を習ったけど、解き方が色々あってどれを使えばいいのか迷ってしまう 平方根を使った解き方でワケが分からなくなった 結局どんな問題で解の公式を使えばいいの? こんな悩みを持っているなら、今回の記事を読んでみてください。 […]
【2次方程式の解】応用問題の解き方
2次方程式の解を利用した応用問題がよくわからない・・・ 2次方程式の解を使ってどう問題を解いたらいいの? こんなお悩みに答えます。 2次方程式の解 を利用した応用問題、例えば $x$の2次方程式 $x^2[…]
【2次方程式の利用】動点P、Qの文章問題
動く点がP、Qの2つある2次方程式がうまく立てられない・・・ 「2次方程式の利用」の動点の文章問題がイマイチわからない! 学校や塾よりもわかりやすく教えてほしい! こういった要望に応えます。 この記事[…]
質問・要望があれば気軽にコメントください👍