2次関数 y = ax² の変域の求め方がよく分からない!
いつも yの変域を間違えて答えちゃうんだけど、なんでだろう?
どうやって解いたら 2次関数 y = ax² の変域がちゃんと出るの?
こういった疑問に答えます。
このページを読めば、例えば
のような「2次関数 y = ax² の変域を求める問題」がスラスラ解けるようになります。
- 1 2次関数 y = ax² のグラフ
- 2 変域(へんいき)とは?
- 3 2次関数 y = ax² の変域の求め方【ポイント】
- 4 2次関数 y = ax² の変域の求め方【練習問題】
- 4.1 【問題1】2次関数 $\displaystyle{ y={1 \over 4} x^2 } $ について、$x$ の変域が $2≦x≦4$ のときの $y$ の変域を求めなさい。
- 4.2 【問題2】2次関数 $y=−2x^2$ について、$x$ の変域が $−1≦x≦2$ のときの $y$ の変域を求めなさい。
- 4.3 【問題3】2次関数 $y=−\displaystyle{ 1 \over 3 } x^2$ について、$x$ の変域が $1≦x≦3$ のときの $y$ の変域を求めなさい。
- 4.4 【問題4】$x$ の変域が $−2≦x≦a$ のとき、2次関数 $y=x^2$ の $y$ の変域は $0≦y≦b$ であり、1次関数 $y=2x+3$ の $y$ の変域は $−1≦y≦c$ である。$b=c$ となる $a$ の値をすべて求めなさい。
- 5 最後に
- 6 【2次関数】変化の割合の簡単な求め方
2次関数 y = ax² のグラフ
2次関数 y = ax² のグラフ のおさらいです。
原点Oを通り、y軸を対称の軸とする放物線で、
比例定数「a」の符号(プラス・マイナス)によって、グラフの開く向き(上・下)が変わります。
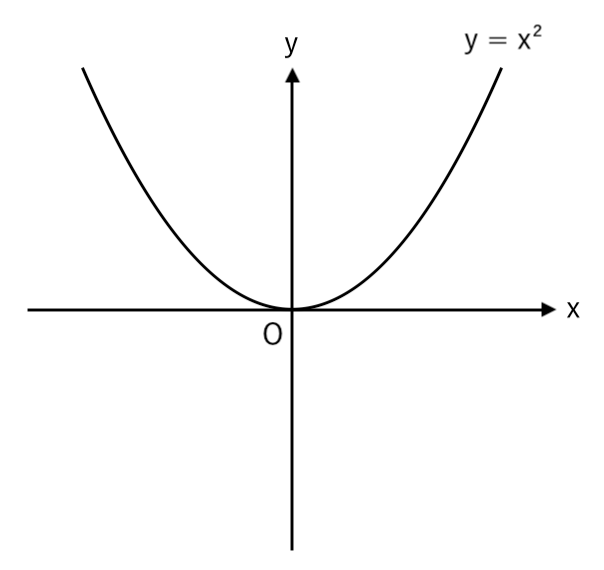
✔︎ a>0(プラス)のとき
上に開く放物線
例:$y=x^2$
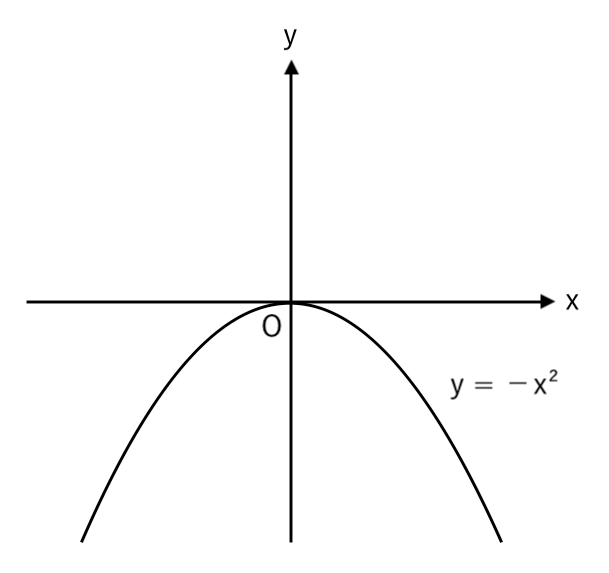
✔︎ a<0(マイナス)のとき
下に開く放物線
例:$y=−x^2$
変域(へんいき)とは?
変域(へんいき)とは、ひとことで言えば「変数( $\color{red}{x, y}$ など)が動く範囲」のことです。
【例1】$x$ の変域が $−1≦x≦2$
「$−1≦x≦2$」は「$x$は $−1$以上 $2$以下」という意味で、
数直線($x$軸)で表すと
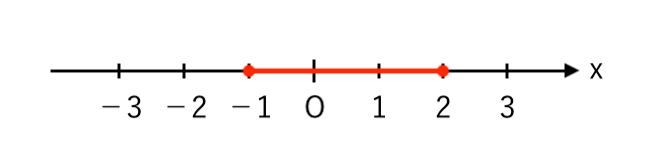
$x$は赤色の部分しか動けないということ。
【例2】$y$ の変域が $0≦y≦4$
「$0≦y≦4$」は「$y$は $0$以上 $4$以下」という意味で、
数直線($y$軸)で表すと
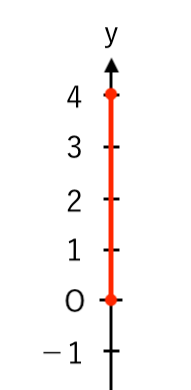
$y$は赤色の部分しか動けないということ。
2次関数 y = ax² の変域の求め方【ポイント】
「2次関数 y = ax² の変域の求め方」のポイントは
$ $ 簡単なグラフをかく
ということです。
【例3】2次関数 $y=x^2$ について、$x$ の変域が $−1≦x≦2$ のときの $y$ の変域は?
具体的な解き方を説明します。
① 2次関数のグラフを点線でかく
2次関数 $y=x^2$ は、
- 原点Oが 頂点
- 上に開く
放物線なので、グラフを点線でかくと
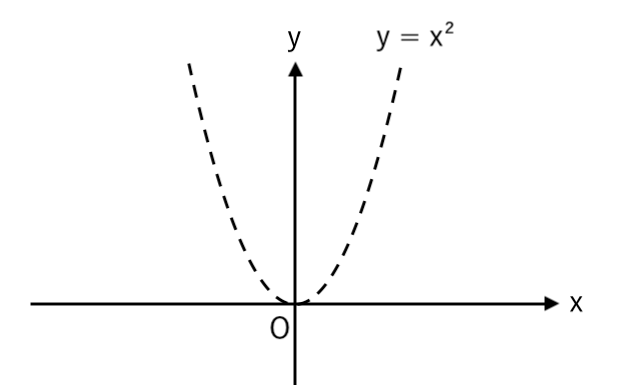
こんな形をしています。
(縦:横 の比率はテキトーでOK)
② $x$ の変域「$−1≦x≦2$」を $x$軸にとる
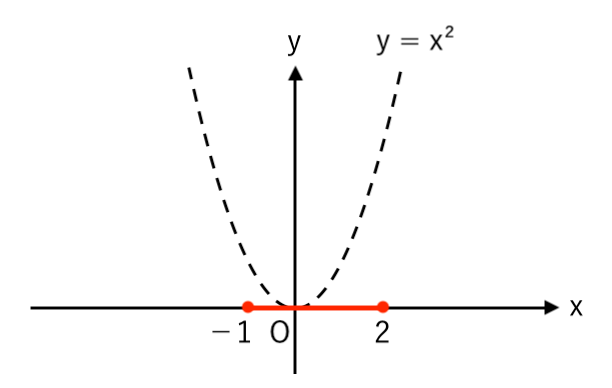
この問題で言うと、左($-1$)はせまく、右($2$)は広い。
③ $x$ の範囲をグラフにとる

④ 高さ($y$座標)が最大・最小の点を読み取る
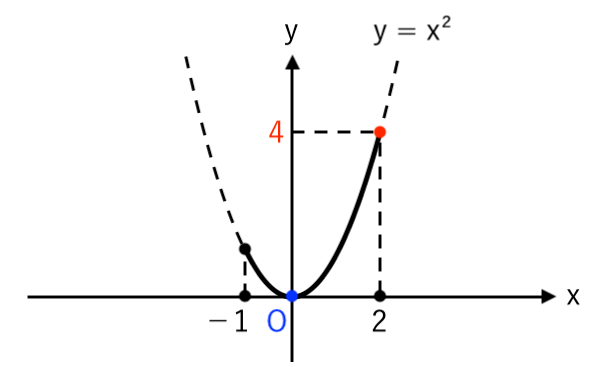
⑤ $y$ の変域は「$ \color{blue}{0}≦y≦\color{red}{4} $」
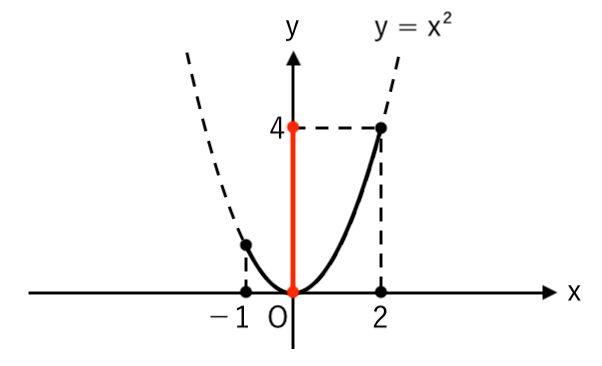
こんな感じでグラフをかくと、正しい答えが導けます。
2次関数 y = ax² の変域の求め方【練習問題】
2次関数 y = ax² の変域の求め方 が分かったところで、さっそく色んなパターンの問題を解いてみましょう。
【問題1】2次関数 $\displaystyle{ y={1 \over 4} x^2 } $ について、$x$ の変域が $2≦x≦4$ のときの $y$ の変域を求めなさい。
実際に簡単なグラフをかいて、高さ($y$座標)が最大・最小の点を読み取ってみましょう。
- 【解答・解説】を見る
-
【解答】$ 1≦y≦4 $
【解説】
簡単なグラフをかくと
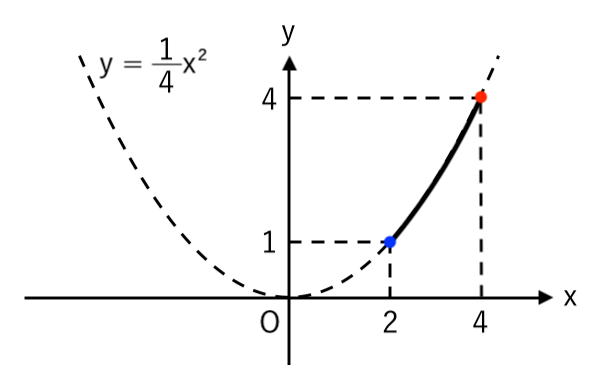
高さが最大・最小の点を読み取ると
$ $ $ \color{blue}{1}≦y≦\color{red}{4} $
【問題2】2次関数 $y=−2x^2$ について、$x$ の変域が $−1≦x≦2$ のときの $y$ の変域を求めなさい。
比例定数「−2」の符号が マイナス なので、グラフは 下に開きます。
- 【解答・解説】を見る
-
【解答】$ −8≦y≦0 $
【解説】
簡単なグラフをかくと
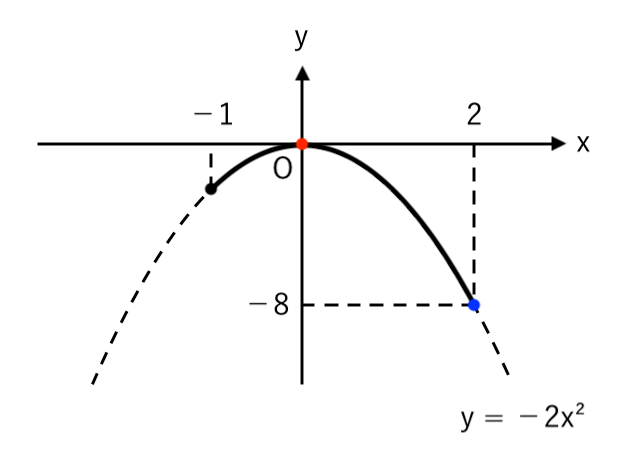
高さが最大・最小の点を読み取ると
$ $ $ \color{blue}{−8}≦y≦\color{red}{0} $
【問題3】2次関数 $y=−\displaystyle{ 1 \over 3 } x^2$ について、$x$ の変域が $1≦x≦3$ のときの $y$ の変域を求めなさい。
- 【解答・解説】を見る
-
【解答】$ \displaystyle{ −3 ≦y≦−{1 \over 3} } $
【解説】
簡単なグラフをかくと
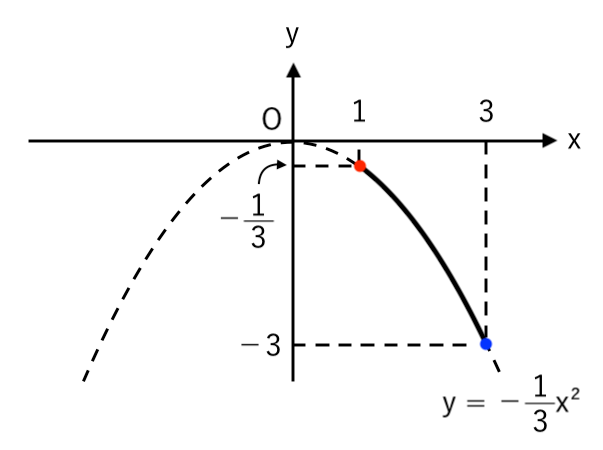
高さが最大・最小の点を読み取ると
$ $ $ \displaystyle{ \color{blue}{ −3 }≦y≦\color{red}{−{1 \over 3} } } $
【問題4】$x$ の変域が $−2≦x≦a$ のとき、2次関数 $y=x^2$ の $y$ の変域は $0≦y≦b$ であり、1次関数 $y=2x+3$ の $y$ の変域は $−1≦y≦c$ である。$b=c$ となる $a$ の値をすべて求めなさい。
ラストは高校入試でも出された問題です。
骨のある応用問題にチャレンジしたいという人は解いてみましょう!
ポイントはやはり「簡単なグラフをかく」ということです。
- 【解答・解説】を見る
-
【解答】$\displaystyle{ a= {1 \over 2} , \enspace 3 }$
【解説】
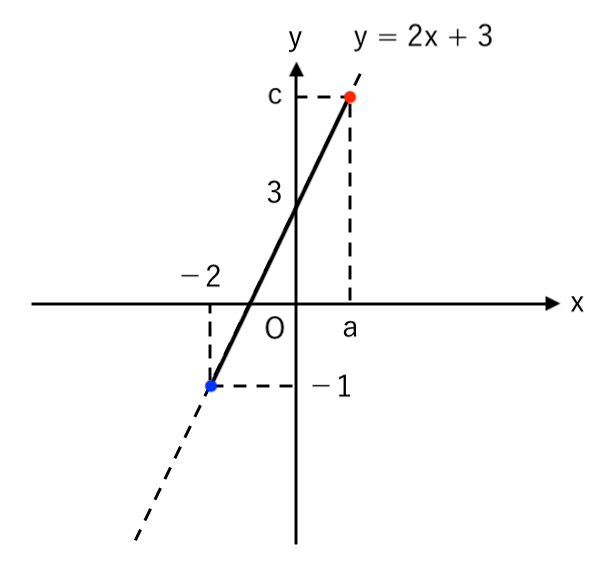
1次関数 $y=2x+3$(右上がりの直線)について
$x$ の変域が「$−2≦x≦a$」のとき
$y$ の変域が「$−1≦y≦c$」なので、
・$x=−2$ のとき $y=−1$ → 点$(−2, −1)$ を通る
・$x=a$ のとき $y=c$ → 点$(a, c)$ を通る
また、2次関数 $y=x^2$ について
$x$ の変域が「$−2≦x≦a$」のとき
$y$ の変域が「$0≦y≦b$」(最小値が $0$)なので、
グラフは 原点O を含む
つまり、$0≦a$($a$ が原点Oよりも右にある、または 原点Oに重なる)
と分かります。
×【NG例】$a<0$のとき、最小値 $0$ にならない
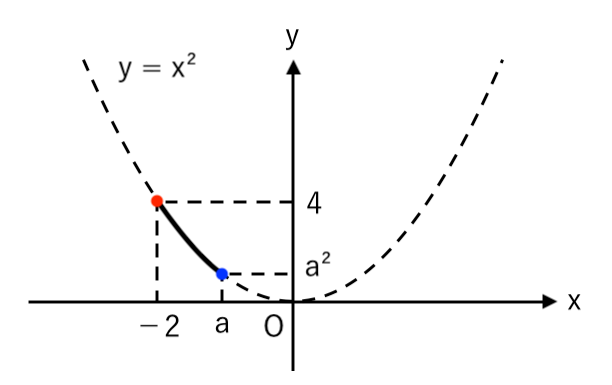
2次関数 $y=x^2$ のグラフが左右対称であることに気をつけると
$ $[1] $0≦a≦2$($a$ が $2$ よりも左にある)
$ $[2] $2<a$ ($a$ が $2$ よりも右にある)
の2通りに場合分けできます。
$ $[1] $0≦a≦2$ のとき
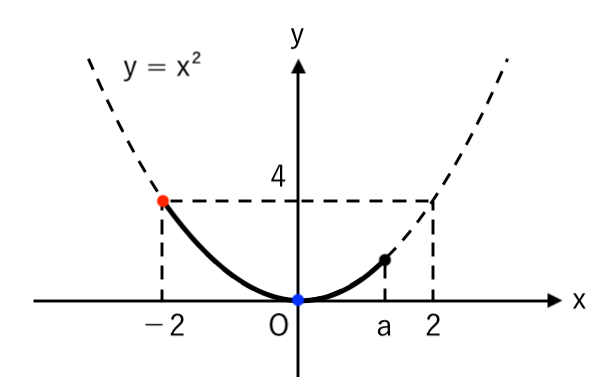
高さが最大・最小の点を読み取ると
$ $ $ \color{blue}{0}≦y≦\color{red}{4} $
一方、2次関数 $y=x^2$ の $y$ の変域が $0≦y≦\color{red}{b}$ より
$ $ $b=4$
さらに、$b=c=\color{red}{4}$ とすると
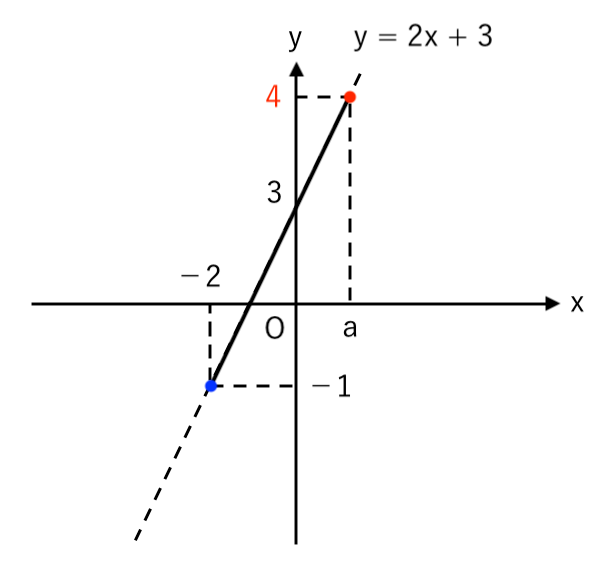
1次関数 $y=2x+3$ は 点$(a, \color{red}{4})$ を通るので、代入して
$ $ $4=2a+3$
$ $ $\displaystyle{ a= {1 \over 2} }$($0≦a≦2$ を満たす)
$ $[2] $2<a$ のとき
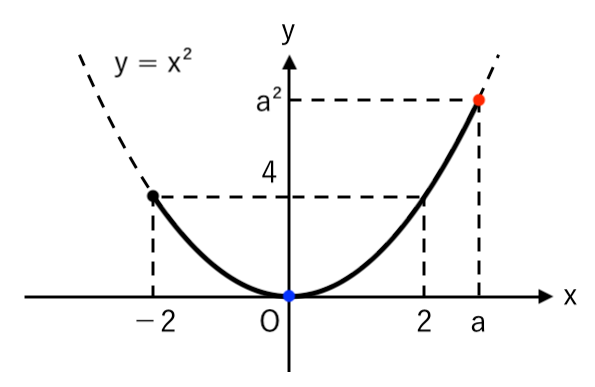
高さが最大・最小の点を読み取ると
$ $ $ \color{blue}{0}≦y≦\color{red}{a^2} $
一方、2次関数 $y=x^2$ の $y$ の変域が $0≦y≦\color{red}{b}$ より
$ $ $b=a^2$
さらに、$b=c=\color{red}{a^2}$ とすると
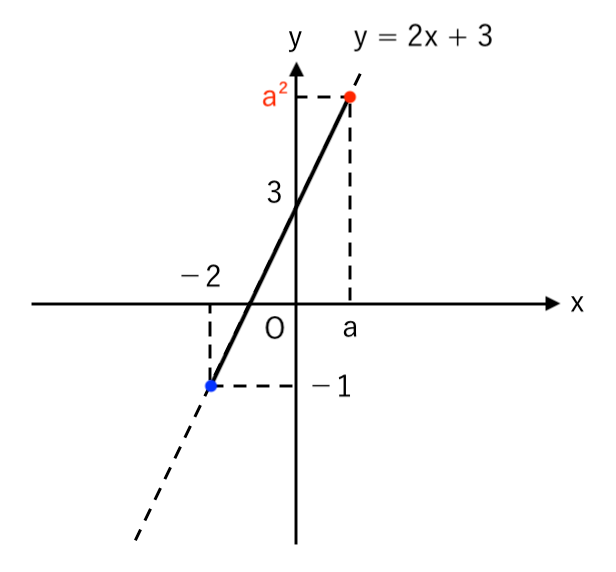
1次関数 $y=2x+3$ は 点$(a, \color{red}{a^2})$ を通るので、代入して
$ $ $ a^2=2a+3 $
$ $ $ a^2 −2a −3 = 0 $
$ $ $ (a + 1)(a − 3) = 0 $
$ $ $ a = −1 , 3 $
$2<a$ より、$ a = 3 $
$ $[1]、[2]より
$ $ $\displaystyle{ a= {1 \over 2} , \enspace 3 }$
どうでしたか? なかなか難しかったですね〜
このように場合分けが必要な問題は、本番でも差がつきます。
高得点を狙いたい人はしっかりマスターしておきましょう!
最後に
最後にまとめです。
「2次関数 y = ax² の変域の求め方」のポイントは
$ $ 簡単なグラフをかく
ということ。
この鉄則を守って、ガッチリ点を取りましょう!
【2次関数】変化の割合の簡単な求め方
「2次関数の変化の割合を簡単に求める裏ワザ」もチェックしておきましょう。
2次関数の「変化の割合」を求める計算が大変だなあ〜 難しくて計算ミスもしそうだし・・・ 2次関数の「変化の割合」の簡単な求め方を教えてほしい! こんなお悩みを解決します。 このページを読んで「2次関数[…]
質問・要望があれば気軽にコメントください👍