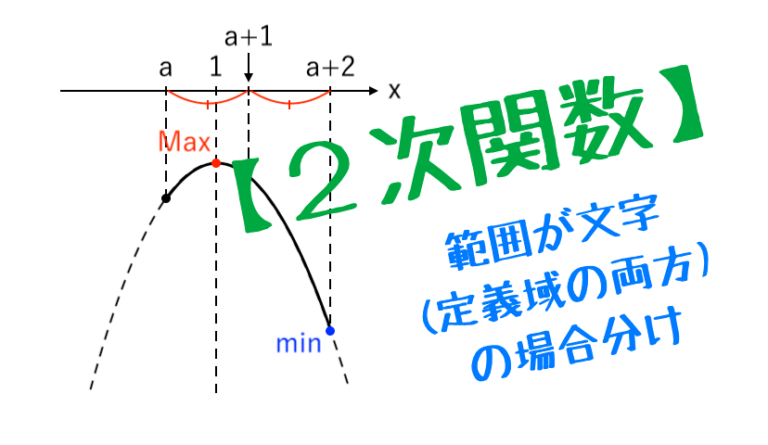
2次関数で、a≦x≦a+2 みたいに範囲が文字のときの場合分けがよく分からない!
定義域の両方に定数aが入っているときの最大値・最小値を求める問題がうまく解けない!
こういったお悩みを解決します。
「2次関数で $a≦x≦a+2$ のように範囲が文字(定義域の両方)のときの場合分け」は、学校のテストや大学入試でよく出る問題のひとつです。
定数 $a$ の値によって $x$ の範囲が動くので、混乱してしまう高校生・受験生はたくさんいます。
一見複雑に見えますが、2次関数の場合分けのやり方にはコツがあります!
このページを読めば、
「2次関数で 範囲が文字(定義域の両方)のときの場合分け」のやり方がスッキリ分かります。
できる限り「丁寧」かつ「シンプルに」分かりやすく説明していきます!
【2次関数】範囲が文字(定義域の両方)のときの場合分け【最大値・最小値】
まず「2次関数の最大値・最小値を求める問題」の場合分けにおける最重要ポイントは
によって場合分けするということです。
さらに、その中でも
- 下に凸 × 最大値
- 上に凸 × 最小値
のパターンの問題で場合分けに必要なのが
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
これらのポイントをしっかり押さえておくと、場合分けがスッキリ理解できるようになります。
2次関数が「下に凸」「上に凸」のパターンに分けてそれぞれ解説していきます!
【2次関数】範囲が文字のときの場合分け(下に凸)
「2次関数(下に凸)の最大値・最小値を求める問題」で
「範囲が文字(定義域の両方)の場合分け」のパターンを見ていきましょう。
【パターン1】下に凸 × 最大値
「下に凸 × 最大値」のパターンは、以下の3つに場合分けできます。
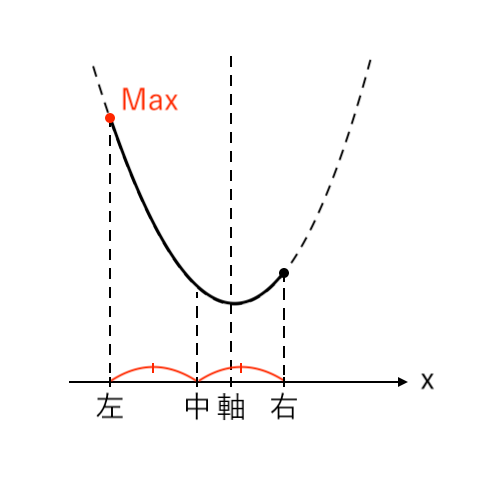
$ $[1] 最大値が「左」(中<軸)
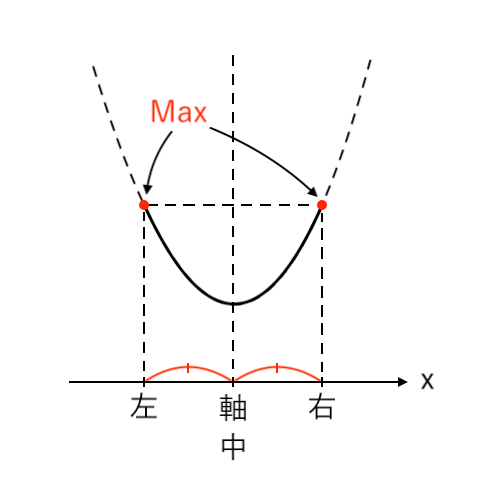
$ $[2] 最大値が「左・右」(軸=中)
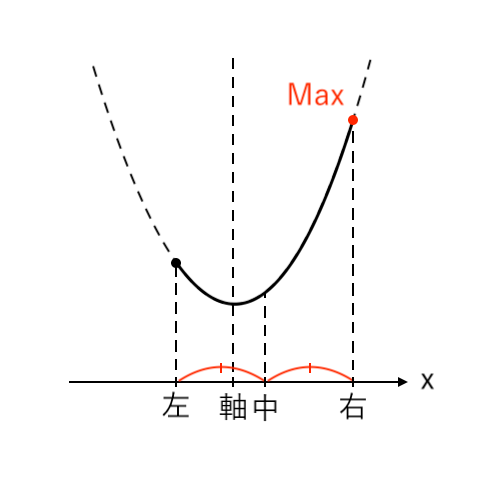
$ $[3] 最大値が「右」(軸<中)
まずは平方完成して
「頂点」「軸」「上・下に凸」
を求めておきましょう。
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。
定数aの値によって定義域が変わるので、場合分けをしなければいけません。
さて、ここで場合分けに必要なのが
ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
Point:最大値(グラフ上で一番高いところ)が「左」「頂点」「右」のどこか?
を考えると
下に凸のグラフなので、最大値が「頂点」の場合はありえませんね。
なので、以下の3つに場合分けします。
$ $[1] 最大値が「左」(中<軸)
$ $[2] 最大値が「左・右」(軸=中)
$ $[3] 最大値が「右」(軸<中)
[1] 最大値が「左」(中<軸)
最大値をとるような $x$ の値が「左($x=a$)」の場合、
「中<軸」より「$a+1<1$」です。
簡単なグラフをかくと

なので、[1]の場合 の解答は以下の通り。
$ $[1] $a+1<1$ すなわち $a<0$ のとき
$ $ $x = a$ で 最大値 $ a^2 -2a + 2 $
あとは、同じ要領で [2]、[3]の場合 も考えればOK!
[2] 最大値が「左・右」(軸=中)
最大値をとるような $x$ の値が「左($x=a$)」と「右($x=a+2$)」の場合(左・右の高さが揃う)を考えます。
このとき、軸と「中」が重なっているので、
「軸=中」より「$1=a+1$」ですね。

$ $[2] $a+1=1$ すなわち $a=0$ のとき
$ $ $x = 0, 2$ で 最大値 $ 2 $ ・・・(注)
(注)「$x=a, a+2$ で 最大値 $a^2 -2a + 2$」に $a=0$ を代入
[3] 最大値が「右」(軸<中)
最大値をとるような $x$ の値が「右($x=a+2$)」の場合
「軸<中」より「$1<a+1$」です。

$ $[3] $1<a+1$ すなわち $0<a$ のとき
$ $ $x = a+2$ で 最大値 $ a^2 +2a + 2 $
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
よって、以下のように場合分けできる。
$ $[1] $a+1<1$ すなわち $a<0$ のとき

$ $ $x = a$ で 最大値 $ a^2 -2a + 2 $
$ $[2] $a+1=1$ すなわち $a=0$ のとき

$ $ $x = 0, 2$ で 最大値 $ 2 $
$ $[3] $1<a+1$ すなわち $0<a$ のとき

$ $ $x = a+2$ で 最大値 $ a^2 +2a + 2 $
$ $[1]〜[3]より、求める最大値は
$ \begin{cases}
a<0 \enspace のとき \enspace \enspace a^2 -2a + 2 \enspace (x = a) \\
\\
a=0 \enspace のとき \enspace \enspace 2 \enspace (x=0, 2) \\
\\
0<a \enspace のとき \enspace \enspace a^2 +2a + 2 \enspace (x = a+2) \\
\end{cases}$
以上、「下に凸 × 最大値」のパターンでした。
【パターン2】下に凸 × 最小値
「下に凸 × 最小値」のパターンは、以下の3つに場合分けできます。
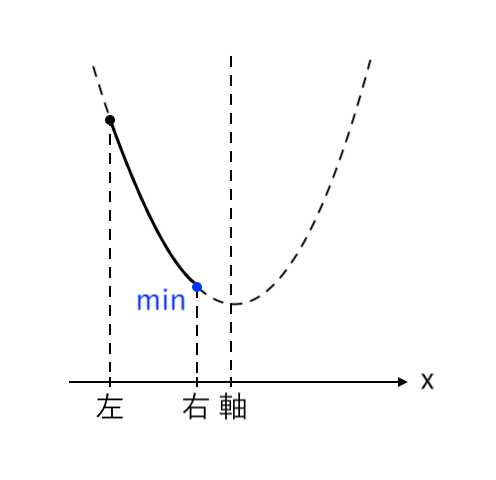
$ $[1] 最小値が「右」(右<軸)
$ $[2] 最小値が「頂点」(左≦軸≦右)
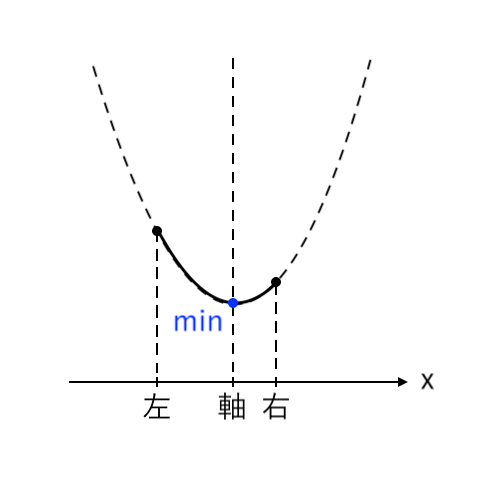
$ $[3] 最小値が「左」(軸<左)
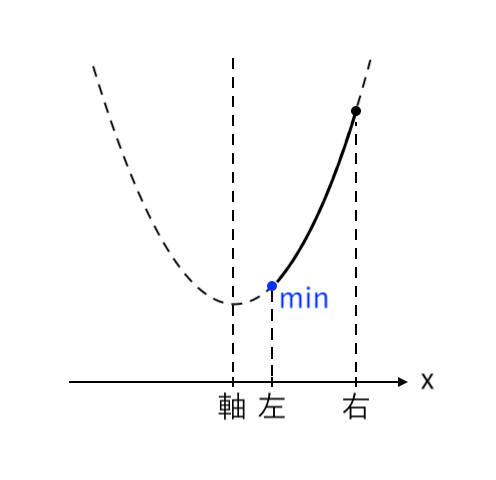
まずは平方完成します。
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。
定数aの値によって定義域が変わるので、場合分けをしなければいけません。
Point:最小値(グラフ上で一番低いところ)が「左」「頂点」「右」のどこか?
を考えると
以下の3つに場合分けできます。
$ $[1] 最小値が「右」(右<軸)
$ $[2] 最小値が「頂点」(左≦軸≦右)
$ $[3] 最小値が「左」(軸<左)
[1] 最小値が「右」(右<軸)
最小値をとるような $x$ の値が「右($x=a+2$)」の場合
「右<軸」より「$a+2<1$」です。

$ $[1] $a+2<1$ すなわち $a<-1$ のとき
$ $ $x = a+2$ で 最小値 $ a^2 +2a + 2 $
[2] 最小値が「頂点」(左≦軸≦右)
最小値をとるような $x$ の値が「頂点($x=1$)」の場合
「左≦軸≦右」より「$a≦1≦a+2$」です。

$ $[2] $a≦1≦a+2$ すなわち $-1≦a≦1$ のとき
$ $ $x = 1$ で 最小値 $ 1 $
(注)不等式「$a≦1≦a+2$」の変形のしかた(解き方)は
$ \begin{cases}
a≦1 \\
\\
1≦a+2 \\
\end{cases}$
∴ $ \begin{cases}
a≦1 \\
\\
-1≦a \\
\end{cases}$
∴ $-1≦a≦1$
[3] 最小値が「左」(軸<左)
最小値をとるような $x$ の値が「左($x=a$)」の場合
「軸<左」より「$1<a$」です。

$ $[3] $1<a$ のとき
$ $ $x = a$ で 最小値 $ a^2 -2a +2 $
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。よって、以下のように場合分けできる。
$ $[1] $a+2<1$ すなわち $a<-1$ のとき

$ $ $x = a+2$ で 最小値 $ a^2 +2a + 2 $
$ $[2] $a≦1≦a+2$ すなわち $-1≦a≦1$ のとき

$ $ $x = 1$ で 最小値 $ 1 $
$ $[3] $1<a$ のとき

$ $ $x = a$ で 最小値 $ a^2 -2a +2 $
$ $[1]〜[3]より、求める最小値は
$ \begin{cases}
a<-1 \enspace のとき \enspace \enspace a^2 +2a + 2 \enspace (x = a+2) \\
\\
-1≦a≦1 \enspace のとき \enspace \enspace 1 \enspace (x=1) \\
\\
1<a \enspace のとき \enspace \enspace a^2 -2a +2 \enspace (x = a) \\
\end{cases}$
以上、「下に凸 × 最小値」のパターンでした。
【パターン3】下に凸 × 最大値・最小値
下に凸の2次関数で「最大値・最小値を同時に答える」パターンの問題です。
【パターン1】と【パターン2】を同時並行で考えていくので、2次関数の中でもレベルが高い問題です。
Point:「左」「頂点」「右」のうち、どこで最大・最小か?
に注目すると、以下の5つに場合分けされます。
| 最大値 | 最小値 | |
| [1] | 左 | 右 |
| [2] | 左 | 頂点 |
| [3] | 左・右 | 頂点 |
| [4] | 右 | 頂点 |
| [5] | 右 | 左 |
$ $[1] 最大値が「左」、最小値が「右」(右<軸)
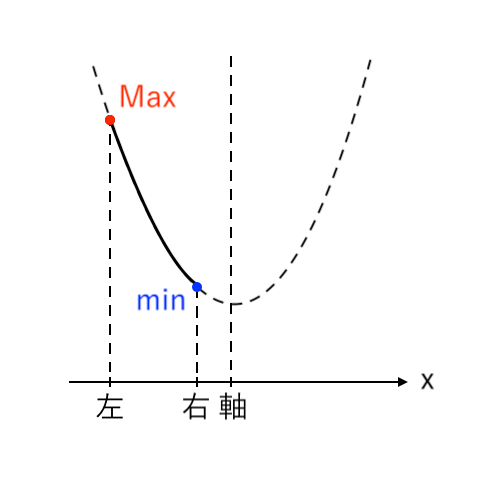
$ $[2] 最大値が「左」、最小値が「頂点」(中<軸≦右)
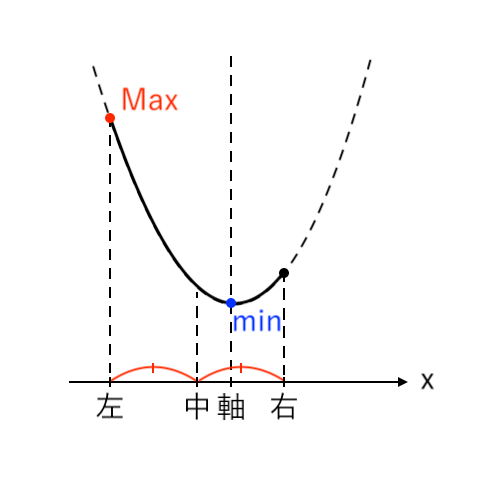
$ $[3] 最大値が「左・右」、最小値が「頂点」(軸=中)
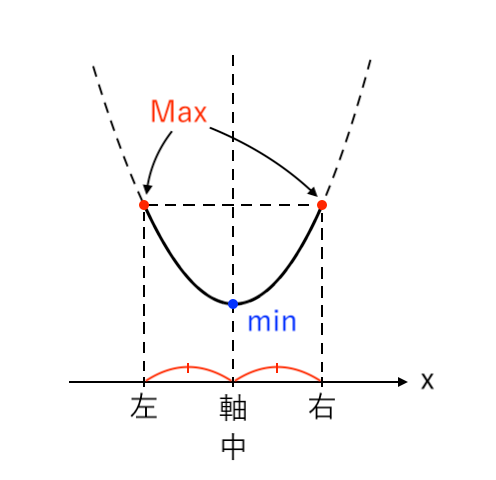
$ $[4] 最大値が「右」、最小値が「頂点」(左≦軸<中)
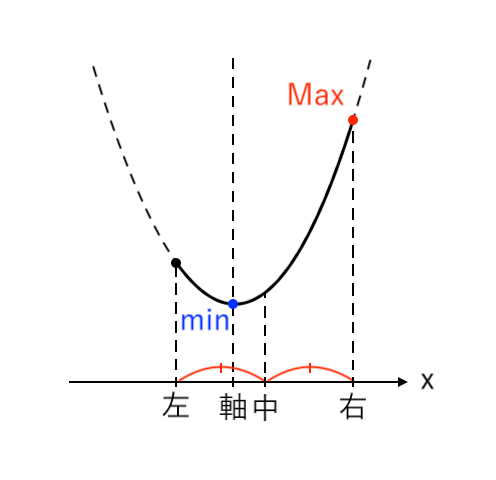
$ $[5] 最大値が「右」、最小値が「左」(軸<左)
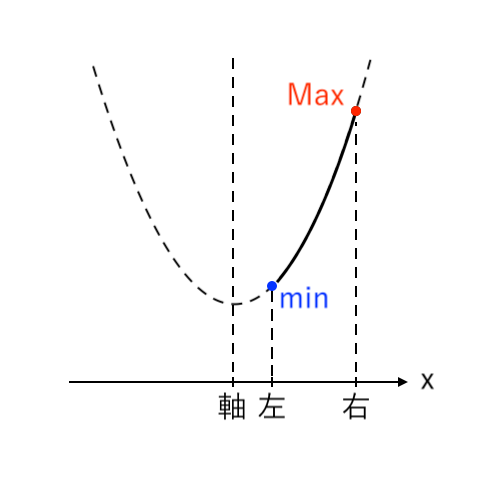
場合分けのしかたが整理できたところで、実際にこの問題をやってみましょう!
まずは平方完成します。
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。
定数aの値によって定義域の位置が変わるので、場合分けをしなければいけません。
さて、その場合分けに必要なのが
ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
ここから、以下の5つに場合分けします。
$ $[1] 最大値が「左」
最小値が「右」(右<軸)
$ $[2] 最大値が「左」
最小値が「頂点」(中<軸≦右)
$ $[3] 最大値が「左・右」
最小値が「頂点」(軸=中)
$ $[4] 最大値が「右」
最小値が「頂点」(左≦軸<中)
$ $[5] 最大値が「右」
最小値が「左」(軸<左)
[1] 最大値が「左」、最小値が「右」(右<軸)
- 左($x=a$)で最大値
- 右($x=a+2$)で最小値
をとる場合、「右<軸」より「$a+2<1$」です。

$ $[1] $a+2<1$ すなわち $a<-1$ のとき
$ $ $x = a$ で 最大値 $a^2 -2a +2$
$ $ $x = a+2$ で 最小値 $a^2 +2a +2$
[2] 最大値が「左」、最小値が「頂点」(中<軸≦右)
- 左($x=a$)で最大値
- 頂点($x=1$)で最小値
をとる場合、
「中<軸≦右」より「$a+1<1≦a+2$」です。

$ $[2] $a+1<1≦a+2$ すなわち $-1≦a<0$ のとき
$ $ $x = a$ で 最大値 $a^2 -2a +2$
$ $ $x = 1$ で 最小値 $1$
(注)不等式「$a+1<1≦a+2$」の変形のしかた(解き方)は
$ \begin{cases}
a+1<1 \\
\\
1≦a+2 \\
\end{cases}$
∴ $ \begin{cases}
a<0 \\
\\
-1≦a \\
\end{cases}$
∴ $-1≦a<0$
[3] 最大値が「左・右」、最小値が「頂点」(軸=中)
- 左($x=a$)・右($x=a+2$)で最大値
- 頂点($x=1$)で最小値
をとる場合、「軸=中」より「$1=a+1$」です。
(左・右の高さが揃う)

$ $[3] $a+1=1$ すなわち $a=0$ のとき
$ $ $x = 0, 2$ で 最大値 $2$
$ $ $x = 1$ で 最小値 $1$
[4] 最大値が「右」、最小値が「頂点」(左≦軸<中)
- 右($x=a+2$)で最大値
- 頂点($x=1$)で最小値
をとる場合、「左≦軸<中」より「$a≦1<a+1$」です。

$ $[4] $a≦1<a+1$ すなわち $0<a≦1$ のとき
$ $ $x = a+2$ で 最大値 $a^2 +2a +2$
$ $ $x = 1$ で 最小値 $1$
[5] 最大値が「右」、最小値が「左」(軸<左)
- 右($x=a+2$)で最大値
- 左($x=a$)で最小値
をとる場合、「軸<左」より「$1<a$」です。

$ $[5] $1<a$ のとき
$ $ $x = a+2$ で 最大値 $a^2 +2a +2$
$ $ $x = a$ で 最小値 $a^2 -2a +2$
ここまでの解答をまとめると以下になります。
- 【解答】を見る
-
【解答】
$ y = x^2 -2x + 2 $
$ $ $ = (x -1)^2 + 1 $
∴ $ \begin{cases}
頂点 \enspace (1, 1) \\
\\
軸:x = 1 \\
\\
下に凸 \\
\end{cases}$ の放物線。ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
よって、以下のように場合分けできる。
$ $[1] $a+2<1$ すなわち $a<-1$ のとき

$ $ $x = a$ で 最大値 $a^2 -2a +2$
$ $ $x = a+2$ で 最小値 $a^2 +2a +2$
$ $[2] $a+1<1≦a+2$ すなわち $-1≦a<0$ のとき

$ $ $x = a$ で 最大値 $a^2 -2a +2$
$ $ $x = 1$ で 最小値 $1$
$ $[3] $a+1=1$ すなわち $a=0$ のとき

$ $ $x = 0, 2$ で 最大値 $2$
$ $ $x = 1$ で 最小値 $1$
$ $[4] $a≦1<a+1$ すなわち $0<a≦1$ のとき

$ $ $x = a+2$ で 最大値 $a^2 +2a +2$
$ $ $x = 1$ で 最小値 $1$
$ $[5] $1<a$ のとき

$ $ $x = a+2$ で 最大値 $a^2 +2a +2$
$ $ $x = a$ で 最小値 $a^2 -2a +2$
$ $[1]〜[5]より、
最大値は
$ \begin{cases}
a<0 \enspace のとき \enspace \enspace a^2 -2a + 2 \enspace (x = a) \\
\\
a=0 \enspace のとき \enspace \enspace 2 \enspace (x=0, 2) \\
\\
0<a \enspace のとき \enspace \enspace a^2 +2a + 2 \enspace (x = a+2) \\
\end{cases}$最小値は
$ \begin{cases}
a<-1 \enspace のとき \enspace \enspace a^2 +2a + 2 \enspace (x = a+2) \\
\\
-1≦a≦1 \enspace のとき \enspace \enspace 1 \enspace (x=1) \\
\\
1<a \enspace のとき \enspace \enspace a^2 -2a +2 \enspace (x = a) \\
\end{cases}$ ・・・(注)(注)このようにまとめて答えてもいいし、別にまとめなくてもOK。
以上、「下に凸 × 最大値・最小値」のパターンでした。
【2次関数】範囲が文字のときの場合分け(上に凸)
次に「2次関数(下に凸)の最大値・最小値を求める問題」で
「範囲が文字(定義域の両方)の場合分け」のパターンを見ていきましょう。
「上に凸」の場合と上下逆さまになるだけで、基本的な考え方は同じです。
【パターン4】上に凸 × 最大値
「上に凸 × 最大値」のパターンは、以下の3つに場合分けできます。
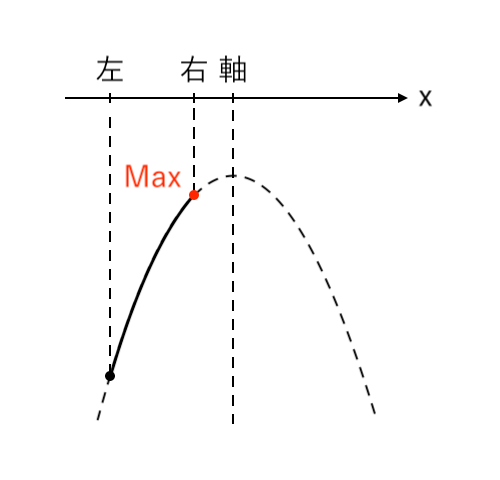
$ $[1] 最大値が「右」(右<軸)
$ $[2] 最大値が「頂点」(左≦軸≦右)
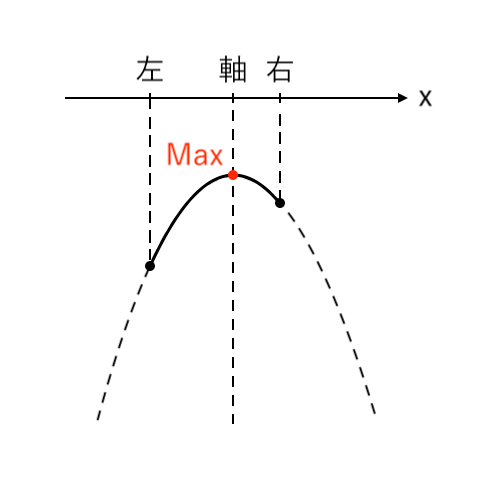
$ $[3] 最大値が「左」(軸<左)
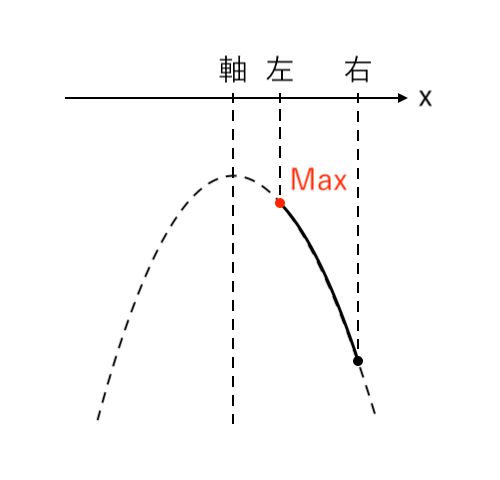
この場合分けをヒントにして解答を作ってみてください。
- 【解答】を見る
-
【解答】
$ y = -x^2 +2x – 2 $
$ $ $= -(x – 1)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (1, -1) \\
\\
軸:x = 1 \\
\\
上に凸 \\
\end{cases}$ の放物線。よって、以下のように場合分けできる。
$ $[1] $a+2<1$ すなわち $a<-1$ のとき

$ $ $x = a+2$ で 最大値 $-a^2 -2a -2$
$ $[2] $a≦1≦a+2$ すなわち $-1≦a≦1$ のとき

$ $ $x = 1$ で 最大値 $-1$
$ $[3] $1<a$ のとき

$ $ $x = a$ で 最大値 $-a^2 +2a -2$
$ $[1]〜[3]より、求める最大値は
$ \begin{cases}
a<-1 \enspace のとき \enspace \enspace -a^2 -2a -2 \enspace (x = a+2) \\
\\
-1≦a≦1 \enspace のとき \enspace \enspace -1 \enspace (x=1) \\
\\
1<a \enspace のとき \enspace \enspace -a^2 +2a -2 \enspace (x = a) \\
\end{cases}$
どうでしたか? 自力で解けましたか?
【パターン5】上に凸 × 最小値
「上に凸 × 最小値」のパターンは、以下の3つに場合分けできます。
$ $[1] 最小値が「左」(中<軸)
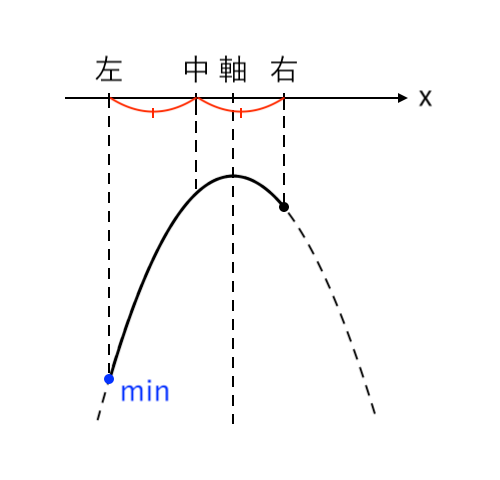
$ $[2] 最小値が「左・右」(軸=中)
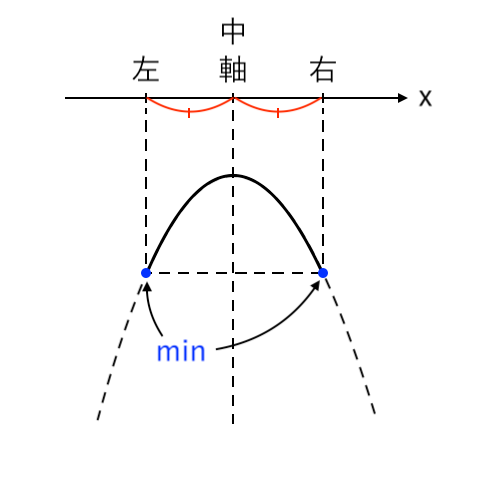
$ $[3] 最小値が「右」(軸<中)
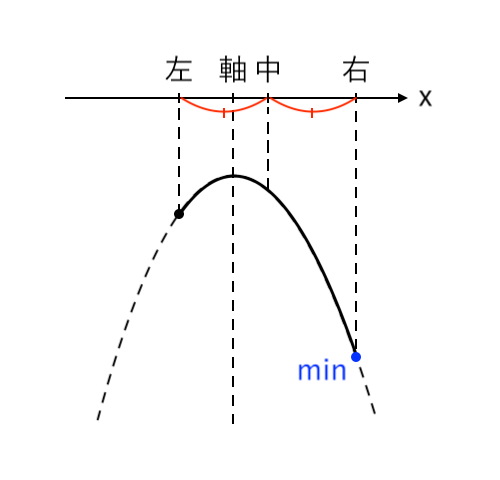
この場合分けをヒントにして解答を作ってみてください。
- 【解答】を見る
-
【解答】
$ y = -x^2 +2x – 2 $
$ $ $= -(x – 1)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (1, -1) \\
\\
軸:x = 1 \\
\\
上に凸 \\
\end{cases}$ の放物線。ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
よって、以下のように場合分けできる。
$ $[1] $a+1<1$ すなわち $a<0$ のとき

$ $ $x = a$ で 最小値 $-a^2 +2a -2$
$ $[2] $a+1=1$ すなわち $a=0$ のとき

$ $ $x = 0, 2$ で 最小値 $-2$
$ $[3] $1<a+1$ すなわち $0<a$ のとき

$ $ $x = a+2$ で 最小値 $-a^2 -2a -2$
$ $[1]〜[3]より、求める最小値は
$ \begin{cases}
a<0 \enspace のとき \enspace \enspace -a^2 +2a -2 \enspace (x = a) \\
\\
a=0 \enspace のとき \enspace \enspace -2 \enspace (x=0, 2) \\
\\
0<a \enspace のとき \enspace \enspace -a^2 -2a -2 \enspace (x = a+2) \\
\end{cases}$
さあ、次はいよいよ最後です!
【パターン6】上に凸 × 最大値・最小値
上に凸の2次関数で「最大値・最小値を同時に答える」パターンの問題です。
【パターン4】と【パターン5】を同時並行で考えていきます。
Point:「左」「頂点」「右」のうち、どこで最大・最小か?
に注目すると、以下の5つに場合分けされます。
| 最大値 | 最小値 | |
| [1] | 右 | 左 |
| [2] | 頂点 | 左 |
| [3] | 頂点 | 左・右 |
| [4] | 頂点 | 右 |
| [5] | 左 | 右 |
$ $[1] 最大値が「右」、最小値が「左」(右<軸)
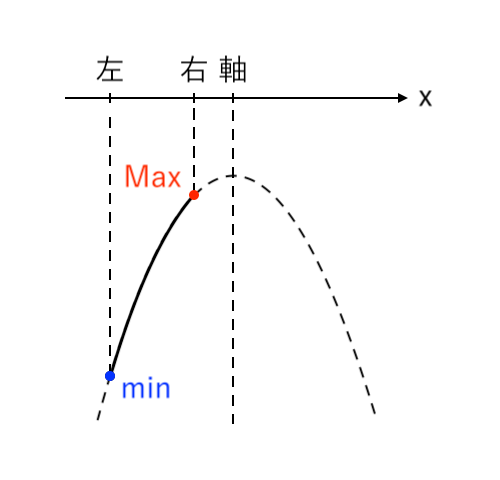
$ $[2] 最大値が「頂点」、最小値が「左」(中<軸≦右)
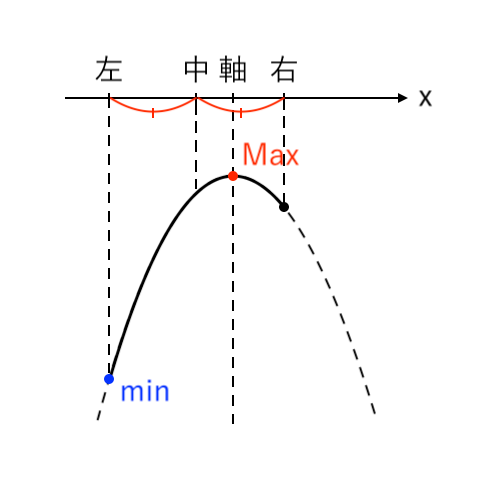
$ $[3] 最大値が「頂点」、最小値が「左・右」(軸=中)
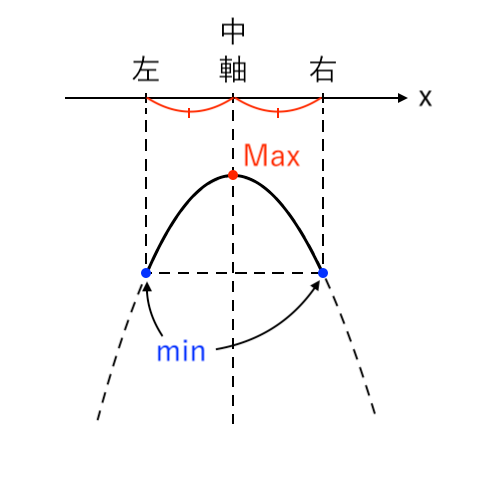
$ $[4] 最大値が「頂点」、最小値が「右」(左≦軸<中)
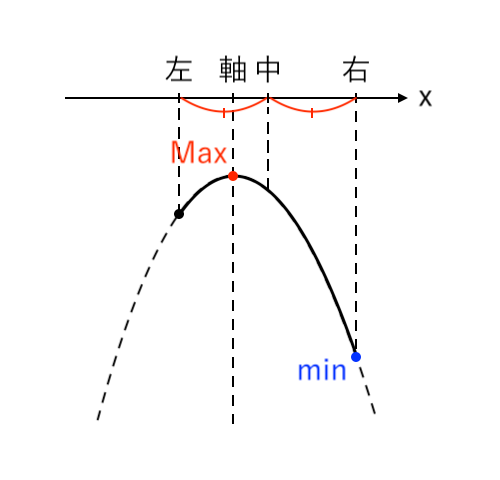
$ $[5] 最大値が「左」、最小値が「右」(軸<左)
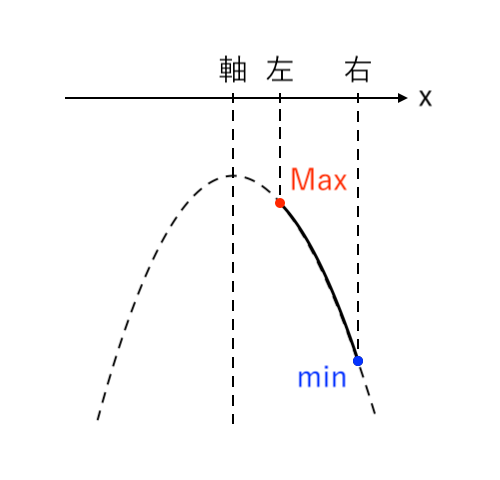
場合分けのしかたが整理できたところで、自力で解いてみましょう!
- 【解答】を見る
-
【解答】
$ y = -x^2 +2x – 2 $
$ $ $= -(x – 1)^2 -1 $
∴ $ \begin{cases}
頂点 \enspace (1, -1) \\
\\
軸:x = 1 \\
\\
上に凸 \\
\end{cases}$ の放物線。ここで、$a≦x≦a+2$ における中央の値は
$ $ $ \displaystyle{ { a + (a+2) \over 2 } = a+1 } $
よって、以下のように場合分けできる。
$ $[1] $a+2<1$ すなわち $a<-1$ のとき

$ $ $x = a+2$ で 最大値 $-a^2 -2a -2$
$ $ $x = a$ で 最小値 $-a^2 +2a -2$
$ $[2] $a+1<1≦a+2$ すなわち $-1≦a<0$ のとき

$ $ $x = 1$ で 最大値 $-1$
$ $ $x = a$ で 最小値 $-a^2 +2a -2$
$ $[3] $a+1=1$ すなわち $a=0$ のとき

$ $ $x = 1$ で 最大値 $-1$
$ $ $x = 0, 2$ で 最小値 $-2$
$ $[4] $a≦1<a+1$ すなわち $0<a≦1$ のとき

$ $ $x = 1$ で 最大値 $-1$
$ $ $x = a+2$ で 最小値 $-a^2 -2a -2$
$ $[5] $1<a$ のとき

$ $ $x = a$ で 最大値 $-a^2 +2a -2$
$ $ $x = a+2$ で 最小値 $-a^2 -2a -2$
$ $[1]〜[5]より、
最大値は
$ \begin{cases}
a<-1 \enspace のとき \enspace \enspace -a^2 -2a -2 \enspace (x = a+2) \\
\\
-1≦a≦1 \enspace のとき \enspace \enspace -1 \enspace (x=1) \\
\\
1<a \enspace のとき \enspace \enspace -a^2 +2a -2 \enspace (x = a) \\
\end{cases}$最小値は
$ \begin{cases}
a<0 \enspace のとき \enspace \enspace -a^2 +2a -2 \enspace (x = a) \\
\\
a=0 \enspace のとき \enspace \enspace -2 \enspace (x=0, 2) \\
\\
0<a \enspace のとき \enspace \enspace -a^2 -2a -2 \enspace (x = a+2) \\
\end{cases}$
以上です。お疲れ様でした!
【まとめ】2次関数の範囲が文字(定義域の両方)の場合分け
最後にまとめです。
「2次関数の最大値・最小値を求める問題」の場合分けのポイントは
によって場合分けするということ。
さらに、その中でも
- 下に凸 × 最大値
- 上に凸 × 最小値
のパターンの問題で場合分けに必要なのが
※ 求め方: $\displaystyle{ 中= { 左 + 右 \over 2 } } $
しっかり覚えておきましょう!
【2次関数】場合分けが「3つ」のパターン
「2次関数の最大値・最小値を求める問題」で場合分けが3つになるパターンがよく分からない・・・ どうやって 3つに場合分けしたらいいの? 教科書や学校の授業だとよく理解できないから、わかりやすく解説してほしい! こういったお悩み[…]
【2次関数】場合分けが「5つ」のパターン
「2次関数の最大値・最小値を求める問題」で場合分けが5つになるパターンが全然分からない・・・ どうやって 5つに場合分けしたらいいの? 3つに分けるパターンとの違いを教えてほしい! 教科書や学校の授業だとよく理解できないから、わ[…]
【2次関数】最大値と最小値の簡単な求め方(手抜きグラフ速答法)
2次関数の「最大値と最小値を求める問題」がよくわからない・・・ グラフを使ってどうやって求めればいいの? 2次関数の最大値と最小値の簡単な求め方を教えてほしい! こういった要望に応えます。 2次関数の[…]
質問・要望があれば気軽にコメントください👍