動く点がP、Qの2つある2次方程式がうまく立てられない・・・
「2次方程式の利用」の動点の文章問題がイマイチわからない!
学校や塾よりもわかりやすく教えてほしい!
こういった要望に応えます。
この記事で解説するのは、2次方程式の利用 における「動点P、Q(2つ)」問題の解き方です。
動く点が2つある問題は、多くの中学生が間違えやすいのでしっかりチェックしましょう。
丁寧にわかりやすく図で説明していきます!
2次方程式「動点P、Q」文章問題の解き方

動点P、Q(2つ)の問題のポイントとしては、
図を描く
ということが必須です。
動く点の問題に限らず、文章問題は
頭の中で考えるのではなく、必ず紙の上で図を描いて考えてください。
そうすると、正答に近づく確率がグッと高まります!
【2次方程式】動点P、Qの問題を解いてみよう
【例題】
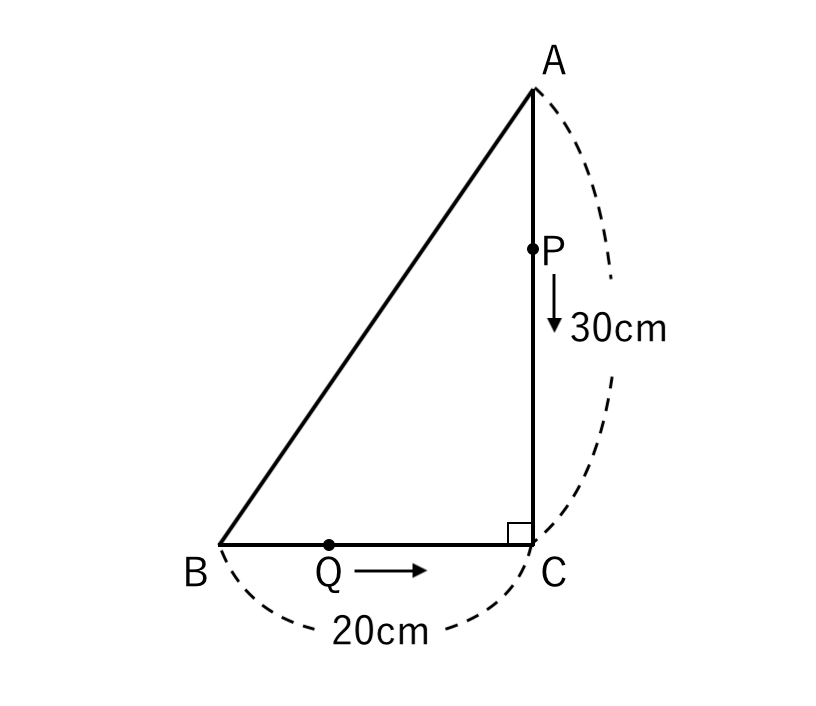
上図のように、BC = $20cm$、AC = $30cm$、∠C = $90°$ の直角三角形ABCがある。
点P、Qは、それぞれ頂点A、Bを同時に出発し、PはAC上を毎秒$3cm$、QはBC上を毎秒$2cm$の速さで、ともに頂点Cまで動く。
このとき、次の問いに答えなさい。
(1) 点P、Qが動き始めてから $x$秒後のとき、線分PCの長さを $x$ を使って表しなさい。
(2) △CPQの面積が$48cm^2$となるのは、点P、Qが動き始めてから何秒後か。
まず、問題文の内容を整理すると、
- 点P、Qは同時にスタート
- 点Pは A → C まで動く
- 点Qは B → C まで動く
- 点Pは毎秒$3cm$で進む
- 点Qは毎秒$2cm$で進む
となります。
ついでに言えば、
つまり、$x$ の変域は
$ $ $0≦x≦10$
ということも分かりますね。
ここまで、問題文が整理できたら準備バッチリ!
(1) PCの長さ
まず $x$秒後の APの長さはいくつになるでしょうか?
点Pは毎秒$3cm$で進むので、
$1$秒後 $3cm$
$2$秒後 $6cm$
$3$秒後 $9cm$
・
・
・
$x$秒後 $3x$ $(cm)$
なので、AP = $3x$ $(cm)$ ですね。
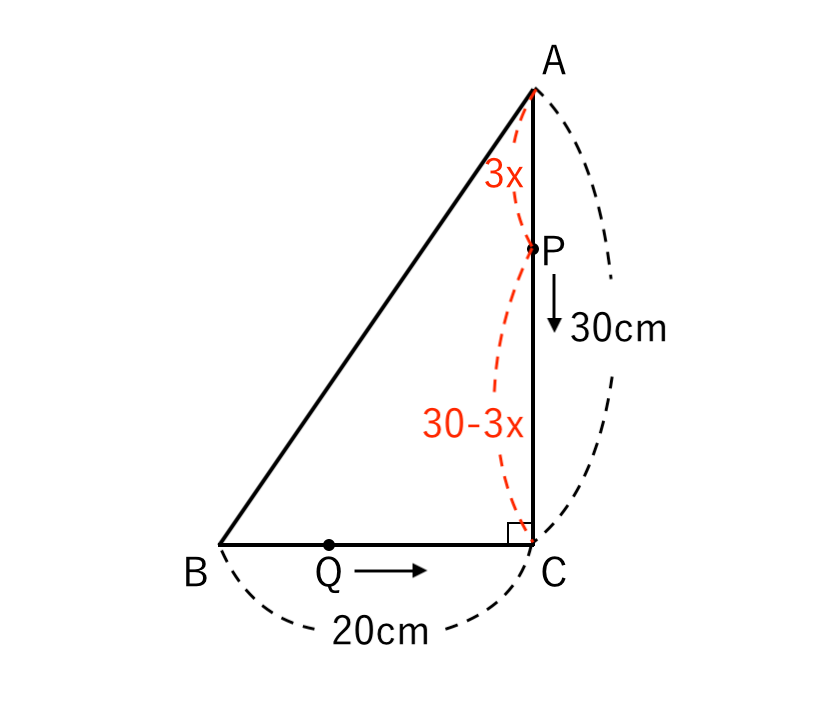
AC = $30cm$ より、
PC = AC – AP
$ $ = $30 – 3x$ $(cm)$
(2) △CPQの面積が$48cm^2$ になるのは何秒後か
$x$秒後の BQの長さを考えると、
点Qは毎秒$2cm$で進むので、
BQ = $2x(cm)$
よって、
QC = BC – BQ
$ $ = $20 – 2x$ $(cm)$
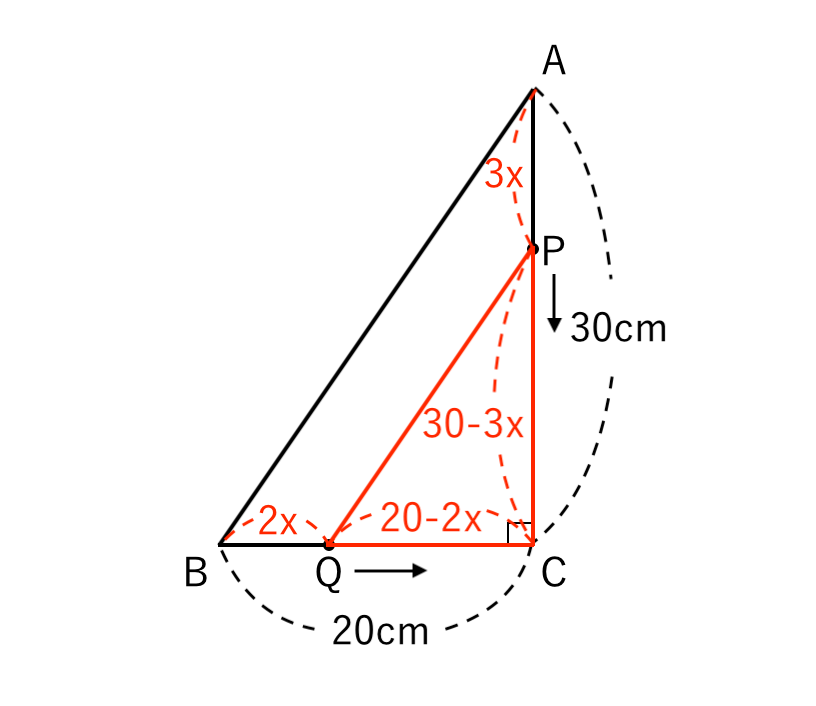
△CPQの面積は、
$(20-2x)(30-3x)÷2$
$= (10-x)(30-3x)$ $(cm^2)$
と表せる。
問題文より、これが $48cm^2$ となるので、
$ $ $(10-x)(30-3x) = 48$
とおける。
この2次方程式を解くと、
$ $ $300 -60x +3x^2 = 48$
$ $ $3x^2 -60x +252 = 0$
両辺を $3$ で割って
$ $ $x^2 -20x +84 = 0$
$ $ $(x – 6)(x – 14) = 0$
$ $ $x = 6, 14$
ここで、これらの x の値が正しいか(問題に合っているか)必ず確認をしましょう。
$x$ の変域は $0≦x≦10$ なので、「$x = 6$」 のみ正しいと言えます。
問題文で「何秒後か?」と聞かれているので、答えは次の通り。
【まとめ】2次方程式「動点P、Q」の解き方
動点P、Qの問題は、
図を描く
という鉄則を守りましょう。
図を描いてから、図形の面積をしっかり考えていくことが大切です。
質問・要望があれば気軽にコメントください👍
2次方程式の利用(文章問題)の解き方
2次方程式の利用(文章問題)をどうやって解いたらいいのか分からない・・・ 自然数とか図形の文章題がニガテでうまく解けないよ〜! テスト・高校入試によくでるパターンの問題をやっておきたい! こんなお悩みを解決します。 &n[…]
参考:二次関数 y = ax²「動点P、Q」の解き方
動く点がP、Qの2つある問題がよくわからない・・・ 動く点が2つあるとき 関数 y = ax² のグラフがうまく描けない! 学校や塾よりもわかりやすく教えてほしい! こういった要望に応えます。 この記[…]