動く点がP、Qの2つある問題がよくわからない・・・
動く点が2つあるとき 関数 y = ax² のグラフがうまく描けない!
学校や塾よりもわかりやすく教えてほしい!
こういった要望に応えます。
この記事で解説するのは、二次関数 $y=ax^2$ における「動く点P、Q(2つ)」問題の解き方(王道・正攻法)です。
テスト・入試でも差がつく問題なので、しっかりマスターしましょう!
心配しなくても大丈夫! 学校・塾よりもわかりやすく&丁寧に解説 します。
二次関数 y = ax²「動く点P、Q(2つ)」の解き方

動く点P、Q(2つ)の問題のポイントとしては、
図を描く
ということが必須です。
大切なことなのでもう一度言いますが、
頭の中で考えるのではなく、必ず紙の上で図を描いて考えてください。
そうすると、正答に近づく確率がグッと高まります!
この鉄則は、動く点がP1つのとき(一次関数)と同様ですね。
一次関数の「動く点P」の問題がよくわからない! グラフの描き方もイマイチ自信がない・・・ 解き方をわかりやすく解説してほしい! こういった要望に応えます。 この記事で解説するのは、一次関数における「動[…]
動く点P、Q(2つ)の問題を解いてみよう
【例題】
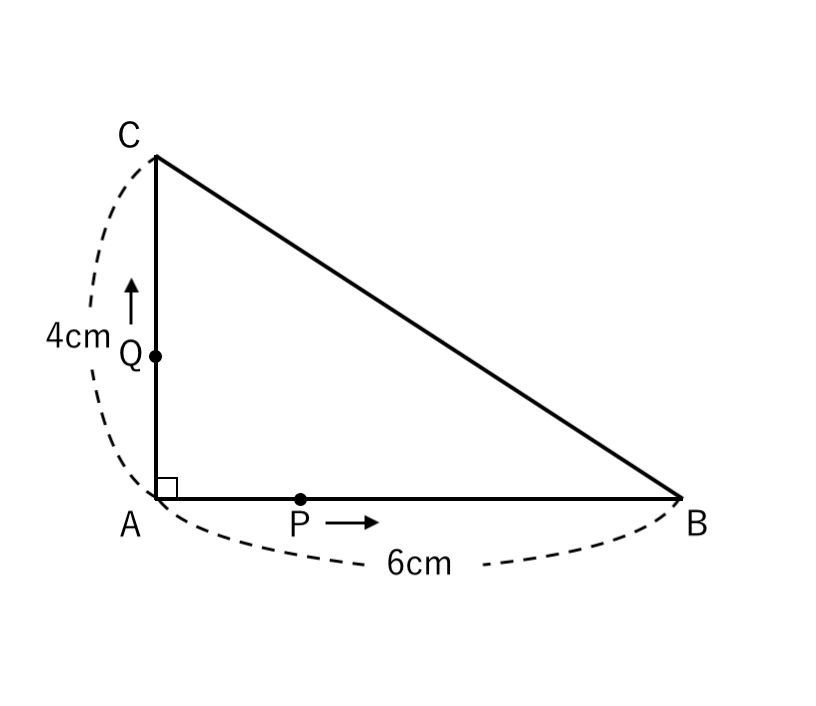
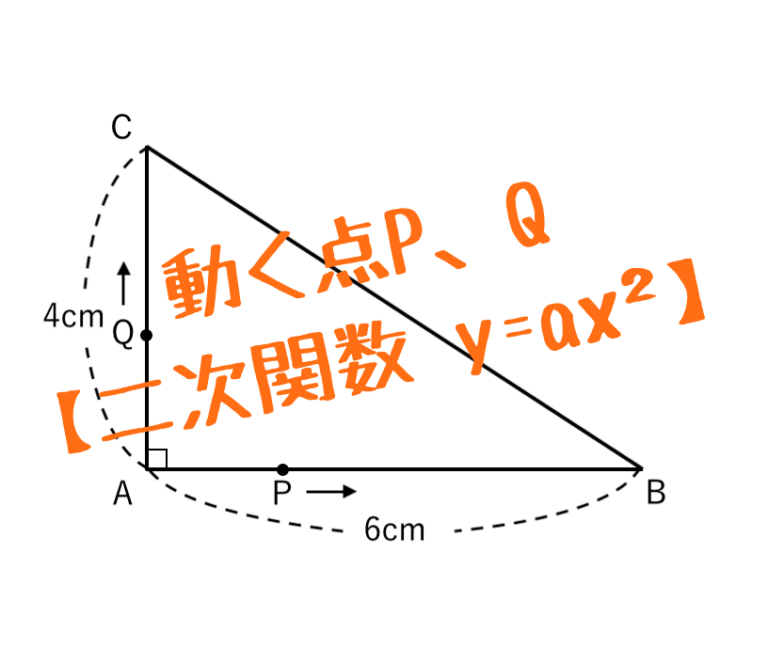
上図のように、AB = $6cm$、AC = $4cm$、∠CAB = $90°$ の直角三角形ABCがある。
点P、Qは頂点Aを同時に出発し、PはAB上、QはAC上を、ともに毎秒$1cm$の速さで、それぞれ頂点B、Cまで動く。
点P、Qが頂点Aを出発してから $x$秒後の△APQの面積を $ycm^2$ とする。
(1) 次のそれぞれの場合について、$y$ を $x$ の式で表しなさい。
(2) $x, y$ の関係を表すグラフをかきなさい。
まず、問題文の内容を整理すると、
- 点P、Qは同時にスタート
- ともに毎秒$1cm$で進む
- 点Pは A → B まで動く
- 点Qは A → C まで動く
- $x$秒後の△APQの面積が $ycm^2$
となります。
(1)①、②のそれぞれの場合について図を描いて解いていきましょう。
(1)① $0 ≦ x ≦ 4$ のとき
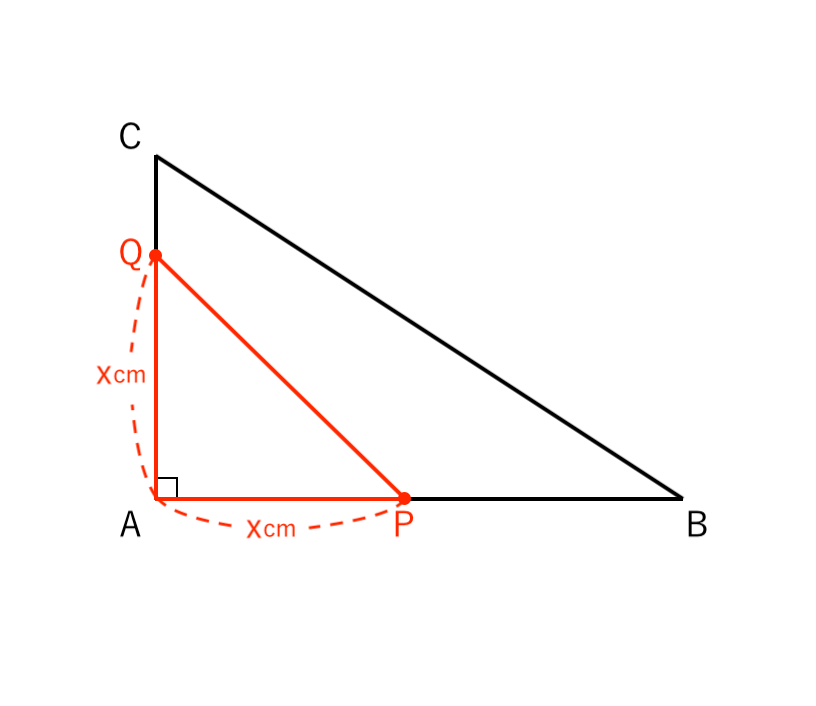
△APQの面積は、
$y = x × x ÷ 2$
(1)① の解答
$$y = {1\over2}x^2$$
(1)② $4 ≦ x ≦ 6$ のとき
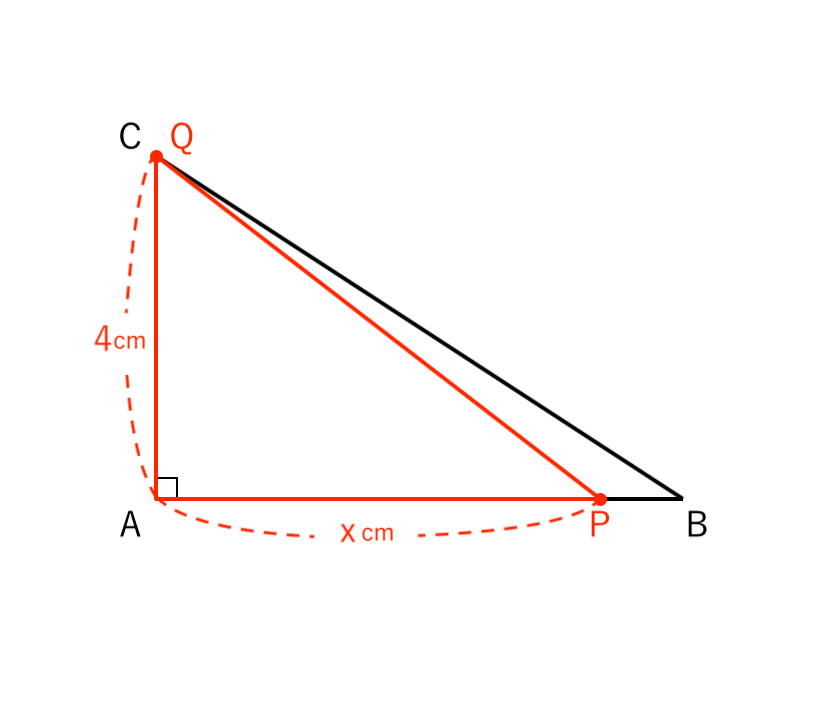
・点Qは、ちょうど4秒後に 頂点Cで止まるので、
AQ = $4(cm)$ で固定されます。
・点Pは、4〜6秒後も 頂点Bに向かって進み続けるので、
AP = $x(cm)$ です。
よって、△APQの面積は、
$y = x × 4 ÷ 2$
(1)② の解答
(2) $x, y$ の関係を表すグラフ
(1)①、②の解答をまとめると、
- $\displaystyle {y= {1\over2}x^2}$($0 ≦ x ≦ 4$のとき)
- $y = 2x$($4 ≦ x ≦ 6$のとき)
2つの場合に分けてグラフを考えましょう。
① $\displaystyle {y= {1\over2}x^2}$($0 ≦ x ≦ 4$のとき)

関数 $\displaystyle {y= {1\over2}x^2}$ は、
- 原点Oを通る、上に開く 放物線
- 点$(2, 2)$、$(4, 8)$を通る
ということを考えながらグラフを描きます。
② $y = 2x$($4 ≦ x ≦ 6$のとき)
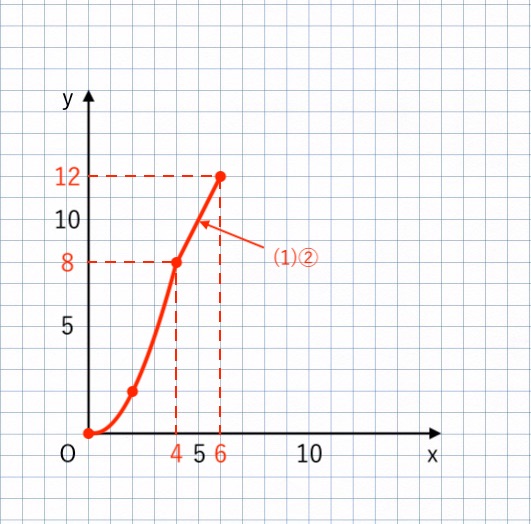
関数 $y = 2x$ は、
- 原点Oを通る、右上がりの 直線
- 点$(4, 8)$、$(6, 12)$を通る
ということを考えながらグラフを描きます。
以上より、問題(2) の解答は以下のようになります。
(2) の解答
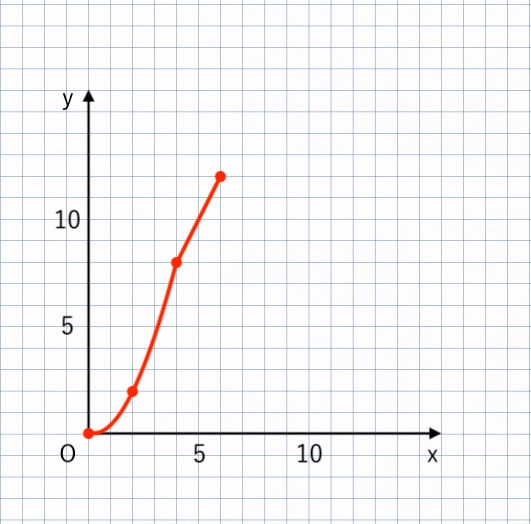
【注意】テストの採点者はどこを見るか?
- 原点、点$(2, 2)$、$(4, 8)$、$(6, 12)$ を通っている
- $0 ≦ x ≦ 4$ のとき 放物線
- $4 ≦ x ≦ 6$ のとき 直線
これらをクリアできていれば、文句なしで完答!
○がもらえます。
【まとめ】「動く点P、Q (2つ)」の解き方
動く点P、Qの問題は、
図を描く
という鉄則を守りましょう。
図を描いてから、三角形の面積をしっかり考えていくことが大切です。
質問・要望があれば気軽にコメントください👍
参考:動く点P(1つ)の問題【裏ワザ】
残念ながら、動く点P、Q(2つ)の問題は上記のような王道(正攻法)しかありませんが、
動く点P(1つ)の問題 のときは王道のやり方ではなく、もっと簡単に&素早く解けてしまう「裏ワザ」もあります。
解く時間を大幅に短縮したい人は、ぜひチェックしておきましょう。
一次関数の「動く点P」の問題がはっきり言って苦手だ どうやって解いたらいいのか分からない、時間がすごくかかってしまう グラフの描き方もイマイチ自信がない・・・ こんな悩みをお持ちの人でも、今回の記事を読めばスッキリ解消します。[…]
参考:【2次方程式の利用】動点P、Qの文章問題
動く点がP、Qの2つある2次方程式がうまく立てられない・・・ 「2次方程式の利用」の動点の文章問題がイマイチわからない! 学校や塾よりもわかりやすく教えてほしい! こういった要望に応えます。 この記事[…]