一次関数の「動く点P」の問題がはっきり言って苦手だ
どうやって解いたらいいのか分からない、時間がすごくかかってしまう
グラフの描き方もイマイチ自信がない・・・
こんな悩みをお持ちの人でも、今回の記事を読めばスッキリ解消します。
ここで紹介するのは、教科書に書いてあるような面倒臭いやり方ではなく、目から鱗(うろこ)の「裏ワザ」と言えるものです。
この方法をマスターすれば、ライバルたちが「動く点Pの問題」を時間をかけて解いているのを横目に見ながら、自分だけ素早く・ミスなく解いてしまうことができます。
なお、教科書に載っているような「王道」の解き方をわかりやすく解説した記事はこちら。
一次関数の「動く点P」の問題がよくわからない! グラフの描き方もイマイチ自信がない・・・ 解き方をわかりやすく解説してほしい! こういった要望に応えます。 この記事で解説するのは、一次関数における「動[…]
なぜ「動く点P」は難しく感じるの?

みんなを悩ませる、動く点Pの問題。
そもそも、なぜ「動く点Pは難しい」と感じてしまうのか?というと「三角形の面積 y を、いきなり x を使って表すから」です。
「え、ちょっと待って。教科書にはそうやって書いてあるよ!」という声が聞こえてきそうですが、そりゃあ学校の教科書には「真面目なやり方」しか書きませんよ。
ですが、教科書のやり方はハッキリ言って分かりづらく、そのせいで「動く点P」に苦手意識を持ってしまう学生が量産されているのも事実です。
そこで今回紹介するのは、教科書には書かれていないような、簡単・スピーディーに解くための完全なる「裏ワザ」です。
「動く点P」の解き方【点の座標→グラフ→式】
動く点Pの問題のポイントは、以下の通り。
- Pの動き方が変わる点の座標を求める
- ①の座標をもとにグラフを描く
- ②のグラフをもとに式を求める
この手順で解きましょう。
それでは、実際に問題を使って説明していきます。
動く点Pの問題を解いてみよう【裏ワザ】
【例題】
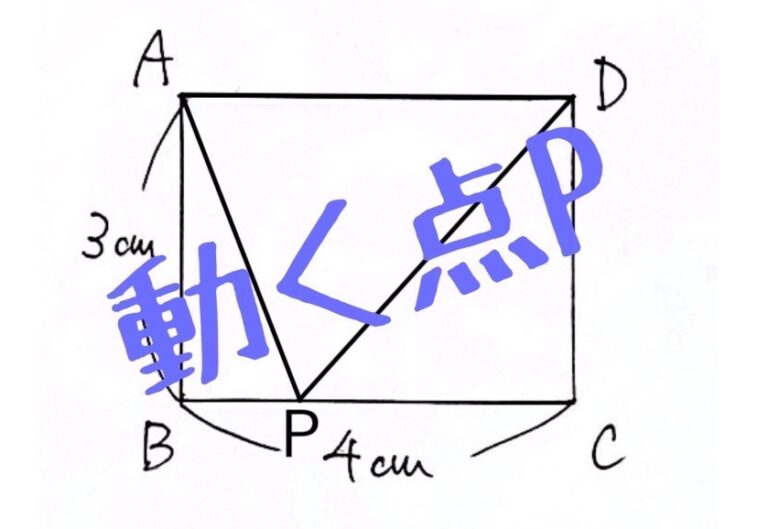
上図のような長方形ABCDの辺上を、毎秒$1cm$の速さで、頂点Aを出発してから、B、Cを通って、Dまで動く点Pがある。
点Pが頂点Aを出発してから $x$秒後の三角形APDの面積を $y cm^2$ とする。
(1) 次のそれぞれの場合について、$y$ を $x$ を使った式で表しなさい。
(2) $x, y$ の関係を表すグラフをかきなさい。
まず、問題文の内容を整理すると、
- 点Pは毎秒$1cm$で進む
- A → B → C → D の順に動く
- $x$秒後の三角形APDの面積が $y cm^2$
となります。
教科書だと、ふつうに (1) から解いていきますが、もちろん今回はそんなことはしません。
この問題では、(2) → (1) の順番で解いていくのが賢いやり方です。
【ステップ1】点の座標を求める
まずは、【ステップ1】Pの動き方が変わる点の座標を求める です。
「Pの動き方が変わる点」は、この問題でいうと「頂点A、B、C、D」の4つです。
Pが頂点A にあるとき
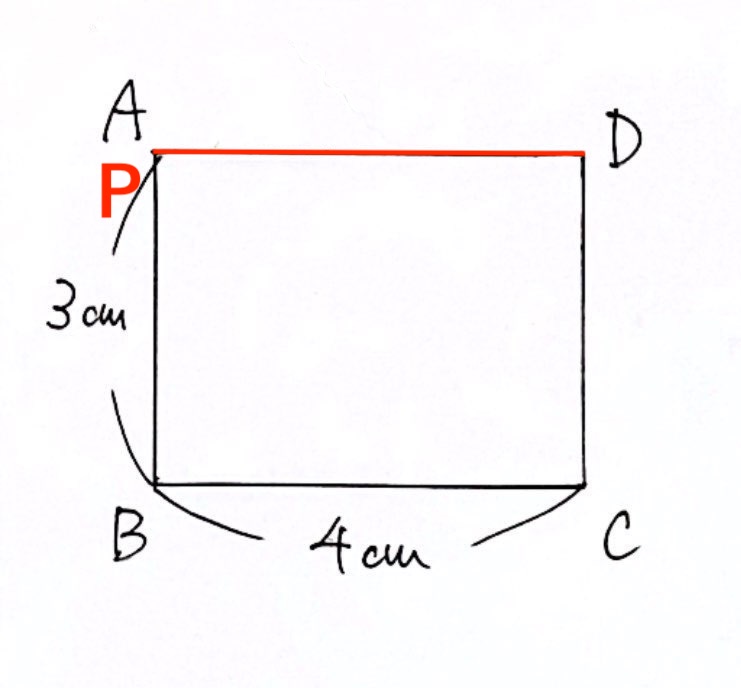
Pが頂点Aにあるとき、
・スタート地点なので、$0$秒後 → $x = 0$
・三角形APDは潰れてしまっているので、面積は $0cm^2$ → $y = 0$
よって、
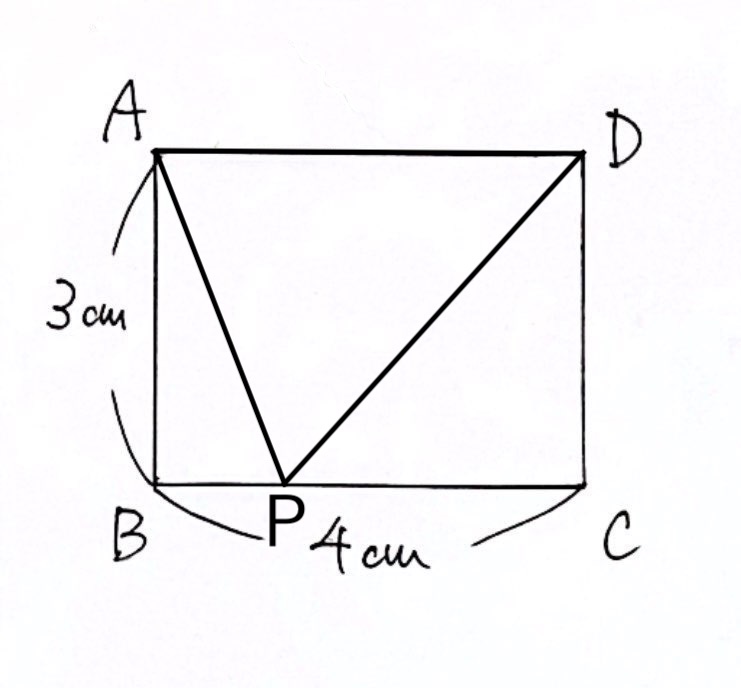
Pが頂点B にあるとき
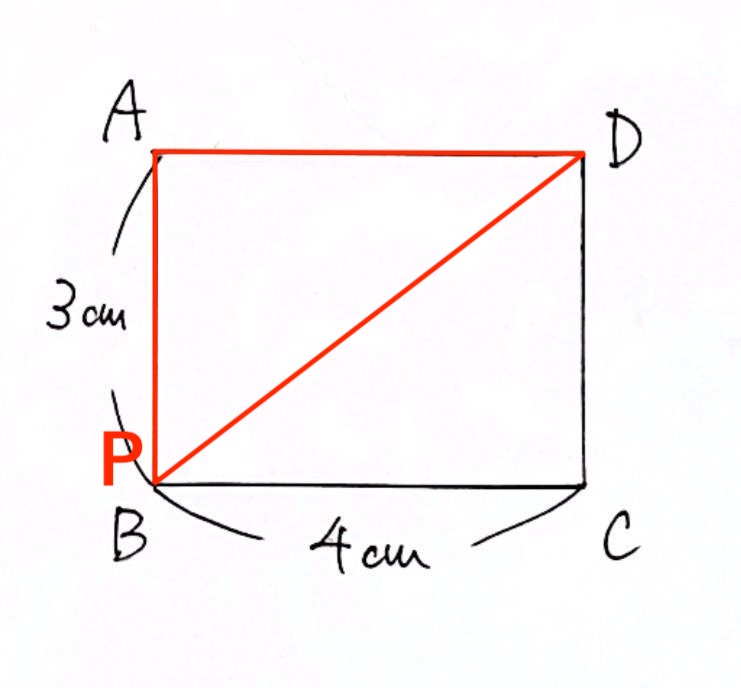
Pが頂点Bにいるとき、
・$3cm$動いたので、$3$秒後 → $x = 3$
・三角形APDの面積は、$4 × 3 ÷ 2 = 6 (cm^2)$ → $y = 6$
よって、
Pが頂点C にあるとき
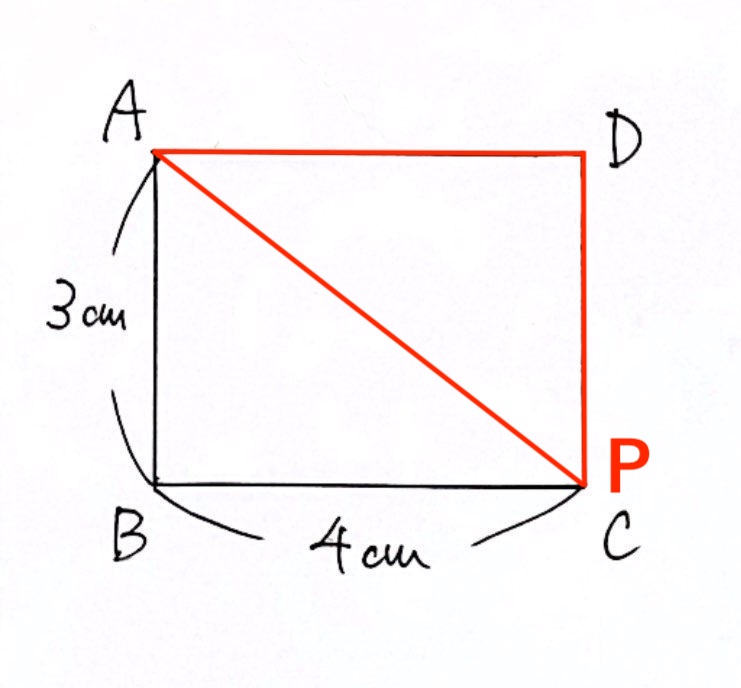
Pが頂点Cにあるとき、
・$3 + 4 = 7 (cm)$ 動いたので、$7$秒後 → $x = 7$
・三角形APDの面積は、$4 × 3 ÷ 2 = 6 (cm^2)$ → $y = 6$
よって、
Pが頂点D にあるとき
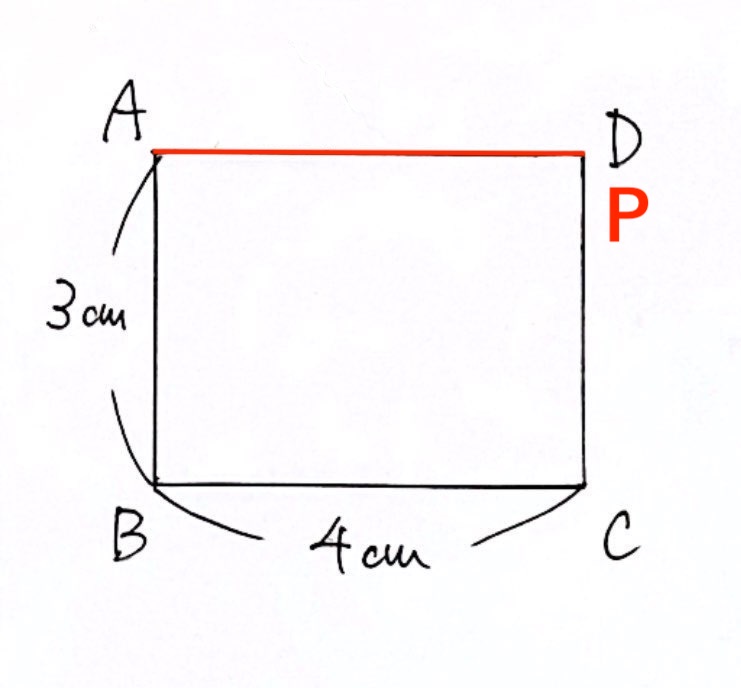
Pが頂点Dにあるとき、
・$3 + 4 + 3 = 10 (cm)$ 動いたので、$10$秒後。→ $x = 10$
・三角形APDは潰れてしまっているので、面積は $0cm^2$ → $y = 0$
よって、
まとめ
点A、B、C、Dの座標をまとめると、
A(0, 0)
B(3, 6)
C(7, 6)
D(10, 0)
となります。
【ステップ2】グラフを描く
【ステップ1】の結果をもとにグラフを描きます。
まずは、点A、B、C、Dの座標をとります。
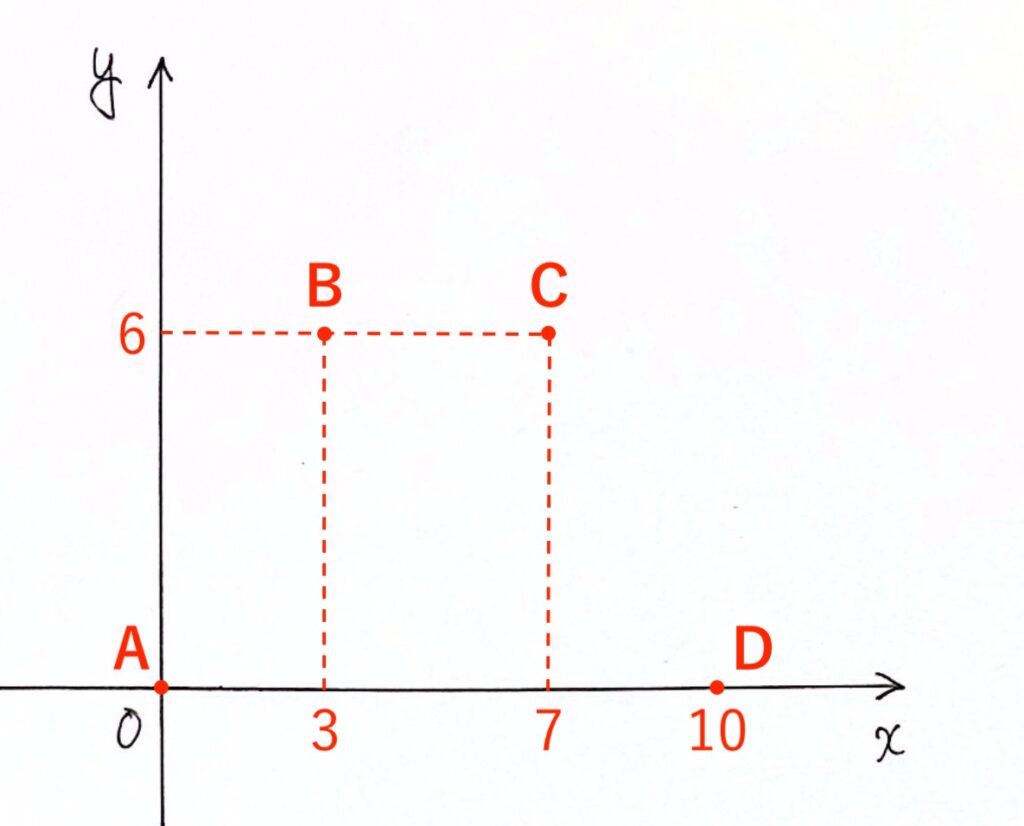
次に、A → B → C → D の順に直線を結びます。
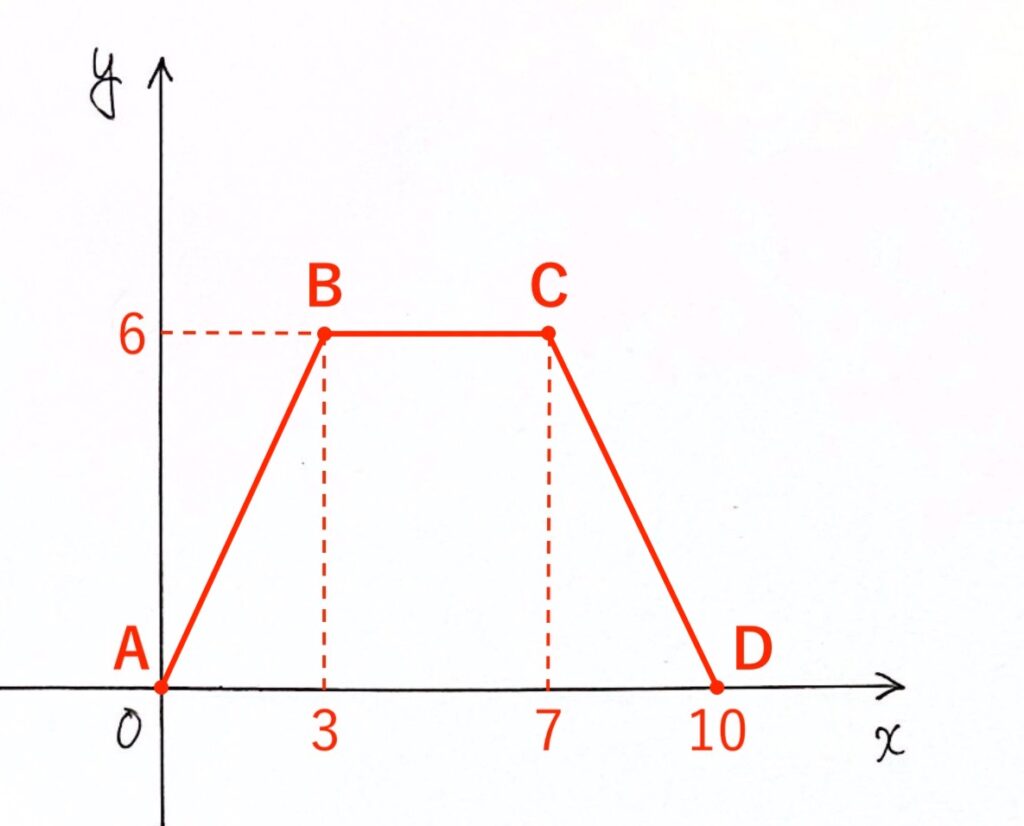
これでグラフは完成です。
以上より、問題(2) の解答は以下のようになります。
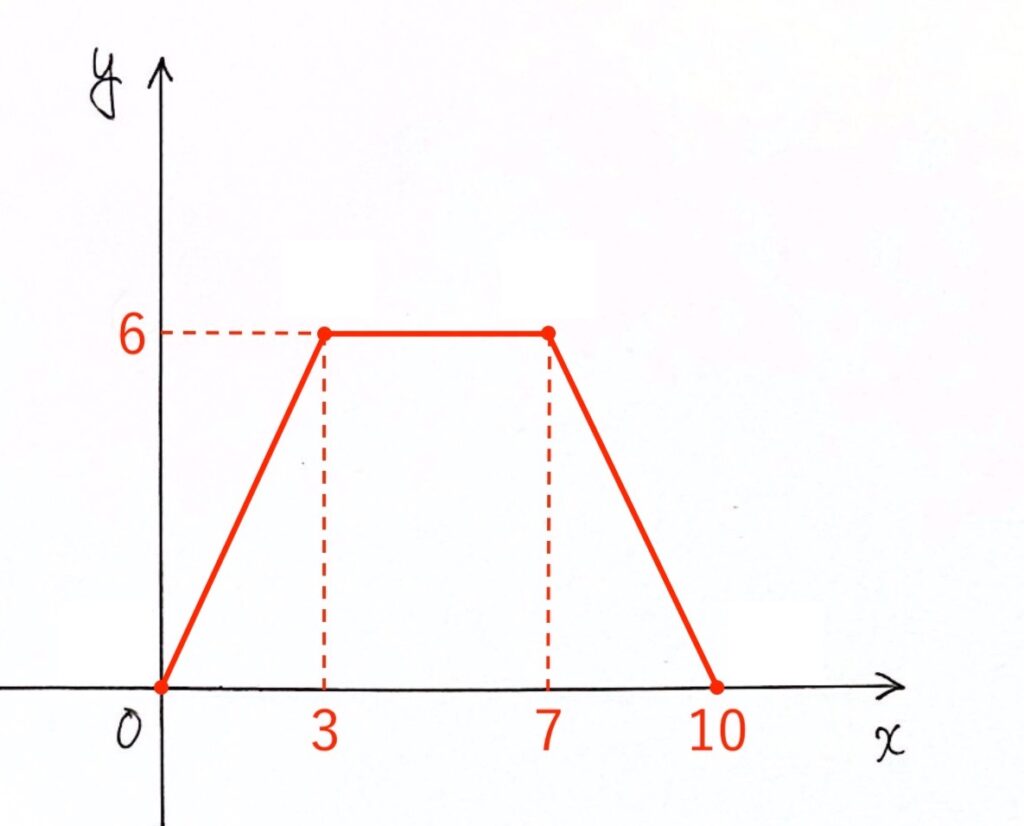
【ステップ3】式を求める
【ステップ2】で描いたグラフをもとに、直線の式を求めていきます。
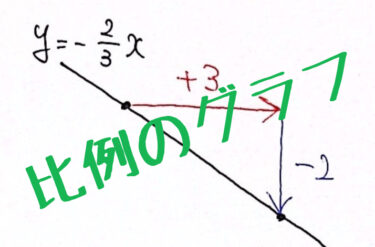
直線の傾きについて復習したい人は、こちらを読んでください。
比例のグラフのかき方、読み取り方がよくわからない 比例定数って何なのかイマイチわからない 直線の傾き、変化の割合と言われてもピンと来ない こういった悩みを持っている人に向けて、この記事を書きました。 「比例とは何か?」から始[…]
問題(1)① 点Pが辺AB上にあるとき
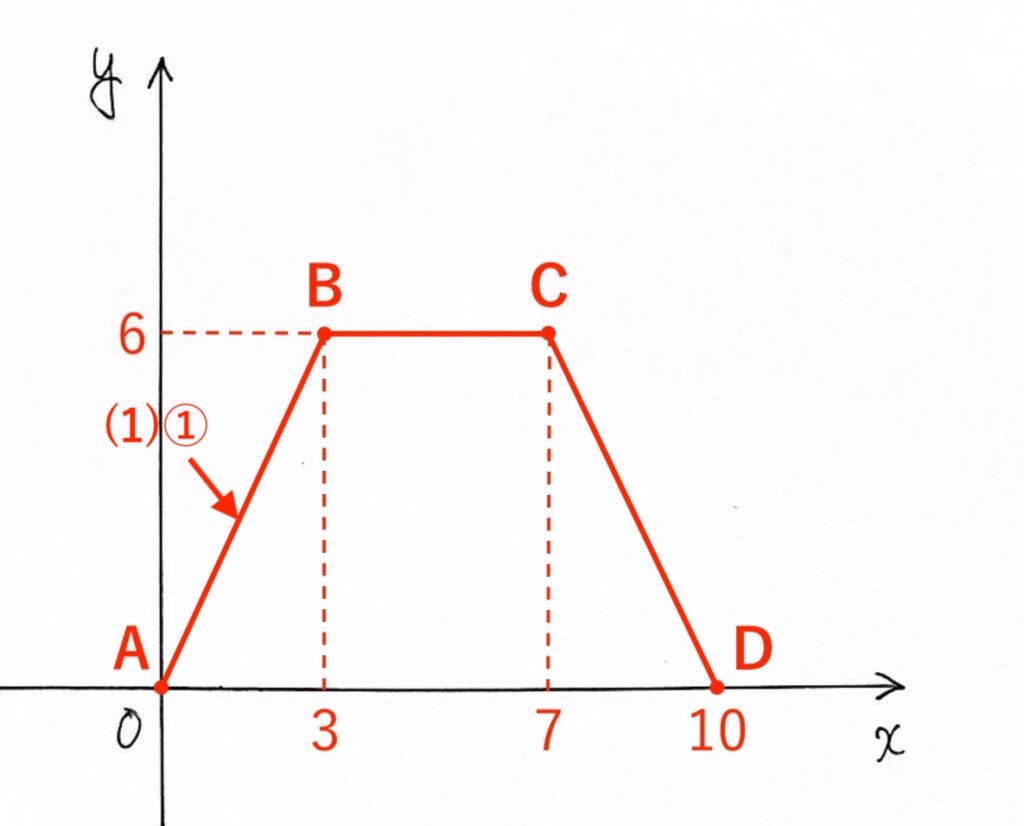
点Pが辺ABにあるのは「0〜3秒後」。定義域で表すと「$0 ≦ x ≦ 3$」です。
このときのグラフは 直線AB です。
直線ABは、2点 A(0, 0)、B(3, 6)を通るので、
傾きは、$${6 \over 3} = 2$$ (右に3、上に6進む)
よって、$y = 2x$ ($0 ≦ x ≦ 3$のとき)
(1)① の解答
$y = 2x$
問題(1)② 点Pが辺BC上にあるとき
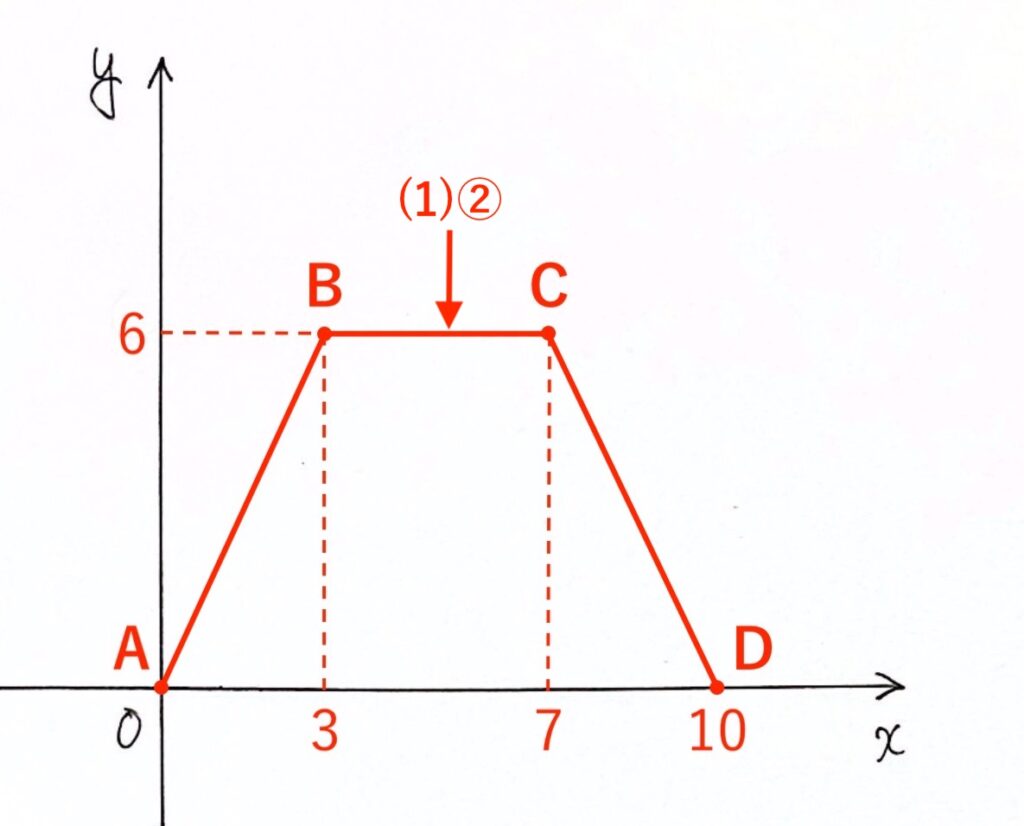
点Pが辺BCにあるのは「3〜7秒後」。定義域で表すと「$3 ≦ x ≦ 7$」です。
このときのグラフは 直線BC です。
直線BCは、2点 B(3, 6)、C(7, 6)を通るので、($y$の値は常に6)
$y = 6$ ($3 ≦ x ≦ 7$のとき)
(1)② の解答
$y = 6$
問題(1)③ 点Pが辺CD上にあるとき
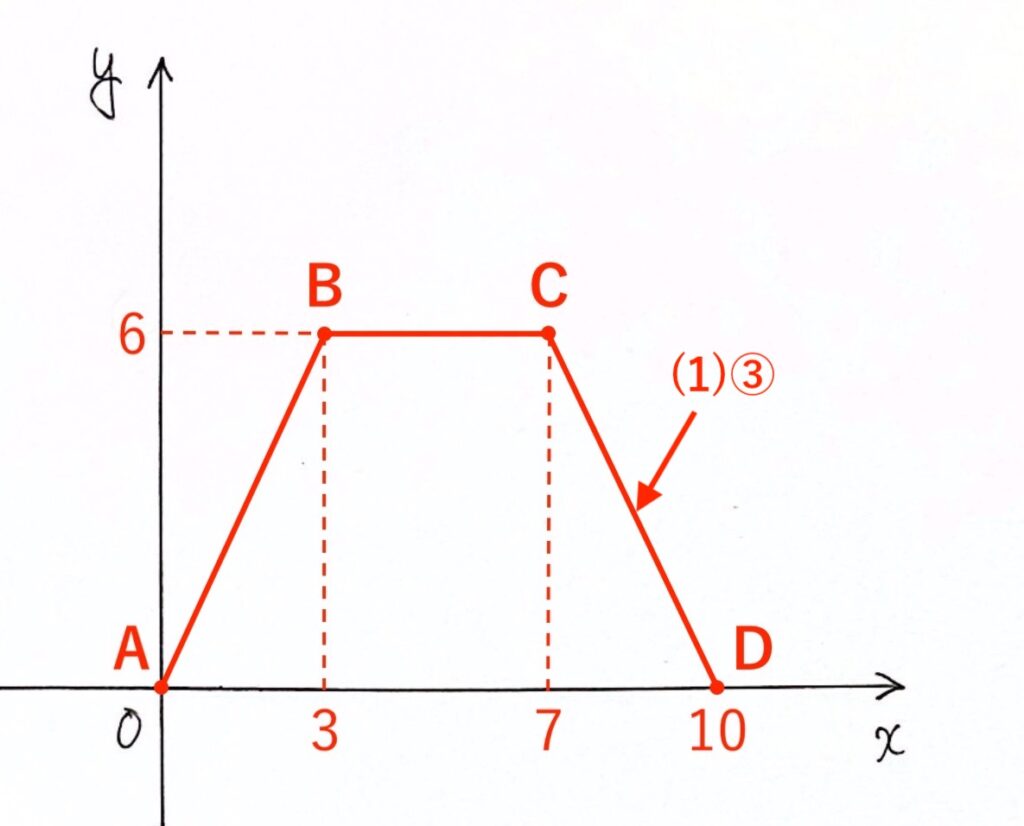
点Pが辺CDにあるのは「7〜10秒後」。定義域で表すと「$7 ≦ x ≦ 10$」です。
このときのグラフは 直線CD です。
直線CDは、2点 C(7, 6)、D(10, 0)を通るので、
傾きは、$$-{6 \over 3} = -2$$ (右に3、下に6進む)
$y = -2x + b$ とおいて、D(10, 0) を代入すると、
$0 = -20 + b$
$b = 20$
よって、$y = -2x + 20$ ($7 ≦ x ≦ 10$のとき)
(1)③ の解答
$y = -2x + 20$
これで、動く点Pの問題がすべて解けました。
【まとめ】「動く点P」の解き方
動く点Pの問題におけるポイントを、改めてまとめておきます。
- Pの動き方が変わる点の座標を求める
- ①の座標をもとにグラフを描く
- ②のグラフをもとに式を求める
この手順を守ることで、素早く・簡単に問題が解けるようになるはずです。
教科書や問題集を使って、慣れるまでたくさん問題を解いてみましょう!
質問・要望があれば気軽にコメントください👍
【発展】面積が○cm² になるのは 何秒後か?
もしこの問題の続きに、
とある場合、どう解いたらよいでしょうか?
問題(1)の①〜③ で場合分けをしてみましょう。
問題(1)① 点Pが辺AB上にあるとき
グラフの式は、
なので、$y = 4$ を代入すると、
$4 = 2x$
$x = 2$
よって、
問題(1)② 点Pが辺BC上にあるとき
グラフの式は、
なので、$y = 4$ となるような xの値 は存在しない。
問題(1)③ 点Pが辺CD上にあるとき
グラフの式は、
なので、$y = 4$ を代入すると、
$4 = -2x + 20$
$2x = 16$
$x = 8$
よって、
まとめ
以上をまとめると、
(3) の解答
2秒後、8秒後
となります。