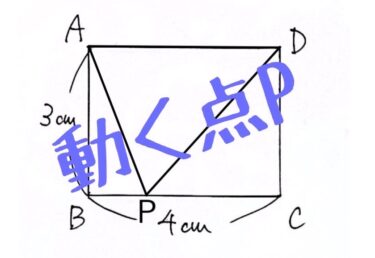
一次関数の「動く点P」の問題がよくわからない!
グラフの描き方もイマイチ自信がない・・・
解き方をわかりやすく解説してほしい!
こういった要望に応えます。
この記事で解説するのは、一次関数における「動く点P」問題の解き方(王道・正攻法)です。
やり方自体は教科書や問題集に載っているのと同様のものですが、学校や塾よりもわかりやすく解説 します。
なお、「王道」ではなく「裏ワザ」の解き方を知りたい人はこちら。
一次関数の「動く点P」の問題がはっきり言って苦手だ どうやって解いたらいいのか分からない、時間がすごくかかってしまう グラフの描き方もイマイチ自信がない・・・ こんな悩みをお持ちの人でも、今回の記事を読めばスッキリ解消します。[…]
ちなみに、中3で習う「二次関数 $y=ax^2$」でも動く点Pは登場します。
スピードが圧倒的に早いのは「裏ワザ」の方ですが、二次関数にも応用が効くのは「王道」のやり方なので、
できればこのページの解き方も理解しておくのがおすすめです。
一次関数「動く点P」の解き方【王道】

動く点Pの問題のポイントとしては、
図を描く
ということが必須です。
大切なことなのでもう一度言いますが、
頭の中で考えるのではなく、必ず紙の上で図を描いて考えてください。
逆に言えば、正しく図を描くことができれば「動く点P」の問題はすでに 半分解けた と言ってもいいでしょう。
動く点Pの問題を解いてみよう【王道】
【例題】
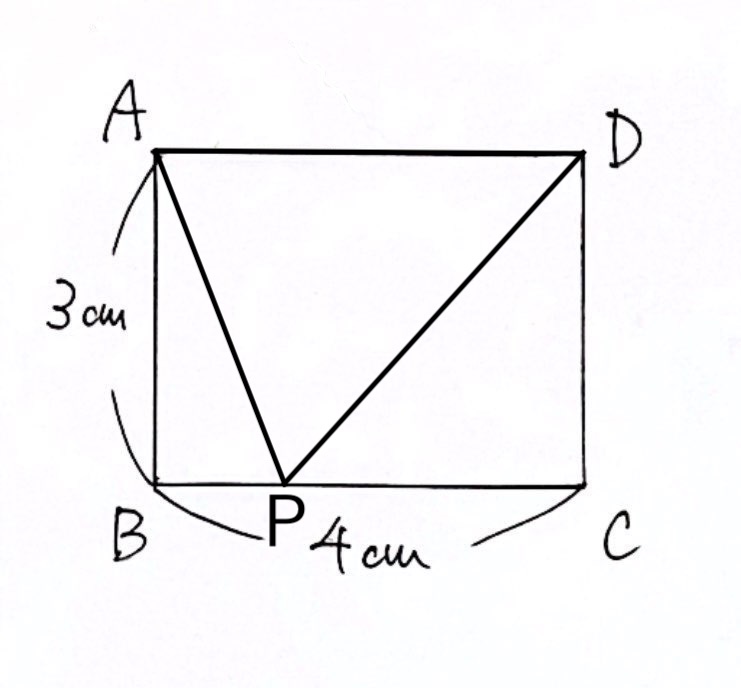
上図のような長方形ABCDの辺上を、$1$秒に$1cm$の速さで、頂点Aを出発してから、B、Cを通って、Dまで動く点Pがある。
点Pが頂点Aを出発してから $x$秒後の△APDの面積を $y cm^2$ とする。
(1) 次のそれぞれの場合について、$y$ を $x$ を使った式で表しなさい。
(2) $x, y$ の関係を表すグラフをかきなさい。
まず、問題文の内容を整理すると、
- 点Pは秒速$1cm$で進む
- A → B → C → D の順に動く
- $x$秒後の三角形APDの面積が $y cm^2$
となります。
さきほど言った通り、(1)①〜③のそれぞれについて図を描いて解いていきましょう。
(1)①点Pが辺AB上にあるとき
・三角形APDの面積は、
$y = 4 × x ÷ 2$
・0〜3秒後なので、$x$ の変域は「$0 ≦ x ≦ 3$」
(1)① の解答
$y = 2x$
(1)②点Pが辺BC上にあるとき
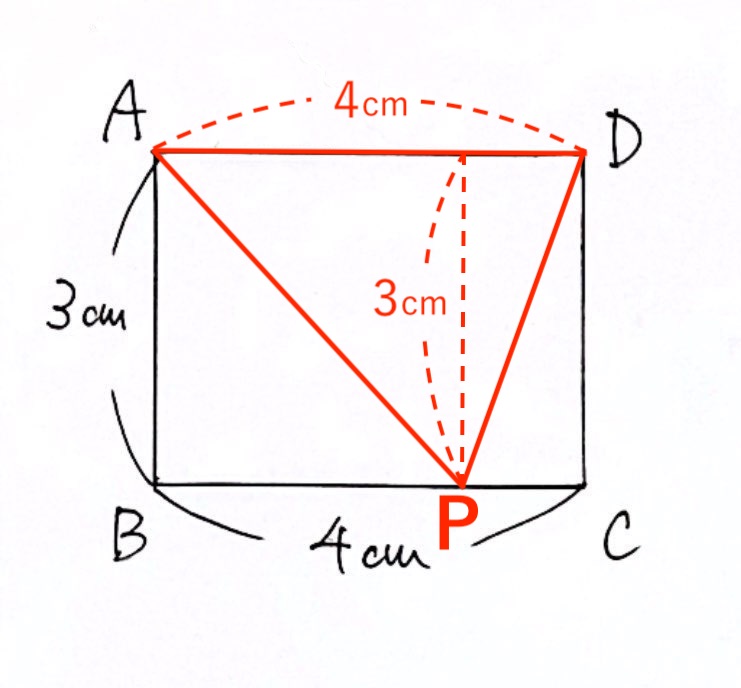
・三角形APDの面積は、
$y = 4× 3 ÷ 2$
・3〜7秒後なので、$x$ の変域は「$3 ≦ x ≦ 7$」
(1)② の解答
$y = 6$
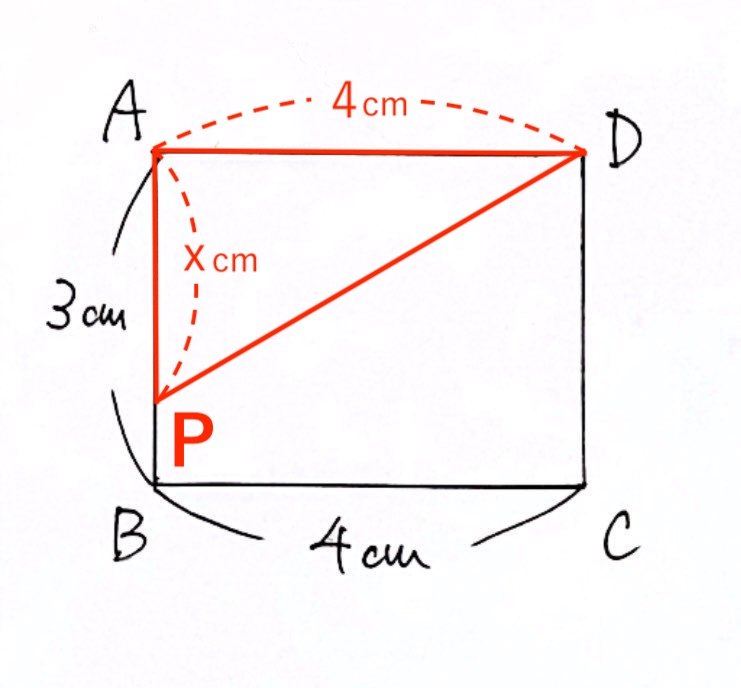
(1)③点Pが辺CD上にあるとき
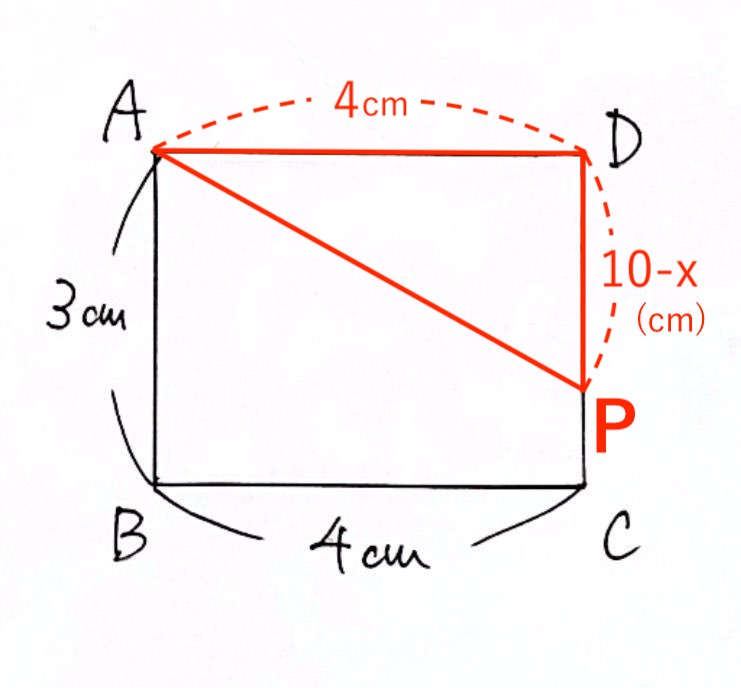
ここは少しコツがいります。
辺PDの長さを $x$ を使って表すと「$10-x$ $(cm)$」になりますが、なぜだか分かりますか?
点A → B → C → D までをビヨーンと延ばして一直線にすると、
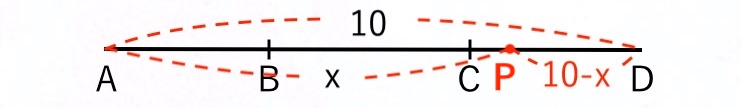
PD = AD – AP
となりますね。
・三角形APDの面積は、
$y = 4× (10-x) ÷ 2$
・7〜10秒後なので、$x$ の変域は「$7 ≦ x ≦ 10$」
(1)③ の解答
$y = -2x+20$
(2) $x, y$ の関係を表すグラフ
(1)①〜③の解答をまとめると、
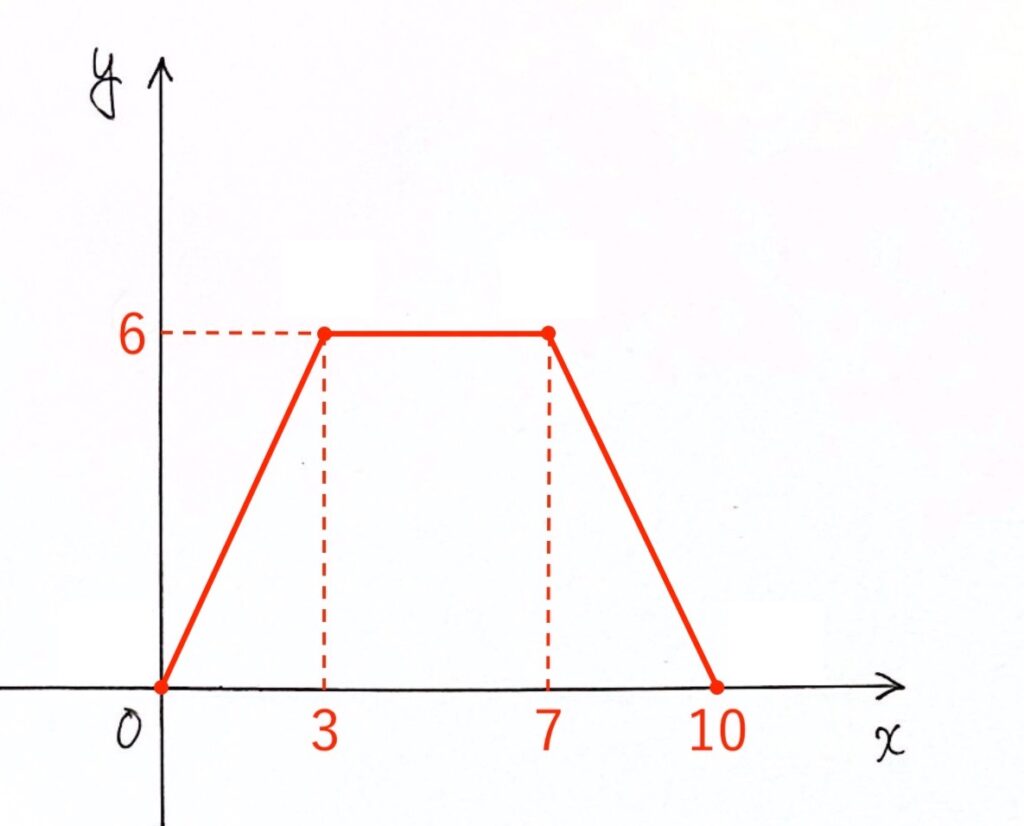
- $y = 2x$($0 ≦ x ≦ 3$のとき)
- $y = 6$($3 ≦ x ≦ 7$のとき)
- $y = -2x+20$($7 ≦ x ≦ 10$のとき)
それぞれ分けてグラフを考えましょう。
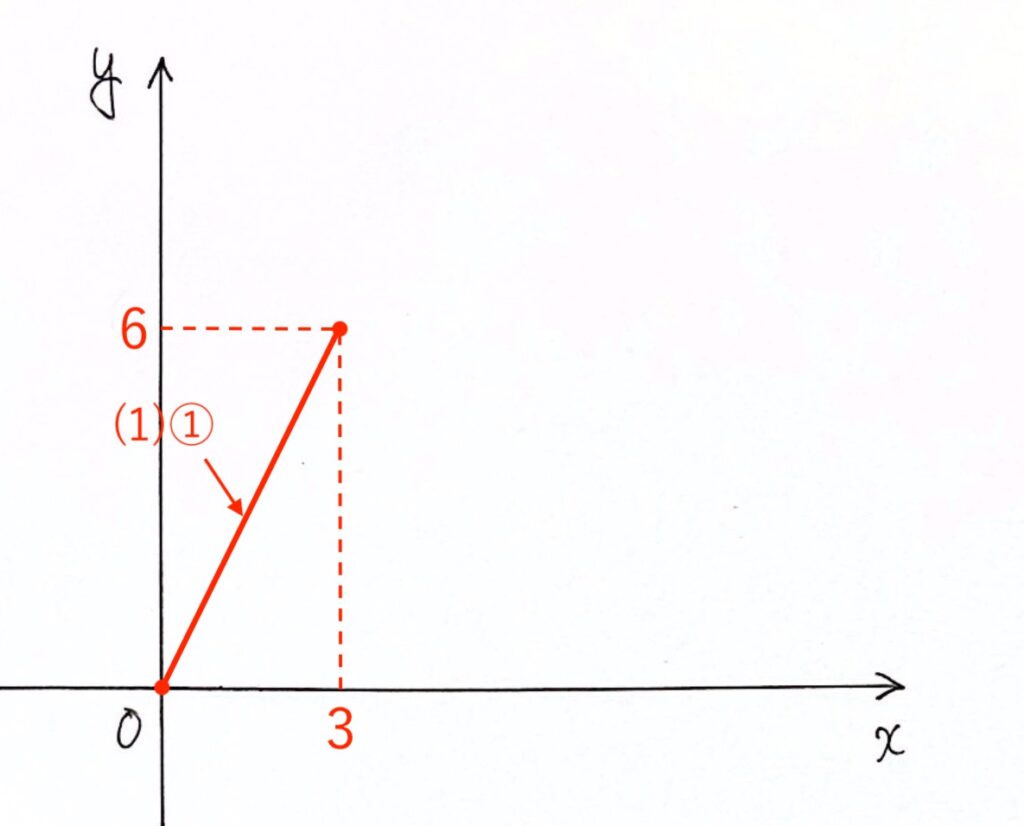
①$y = 2x$($0 ≦ x ≦ 3$のとき)
傾きが $2$ で、原点Oを通る直線(比例)なので、
点(0, 0) から 点(3, 6) まで直線で結びます。
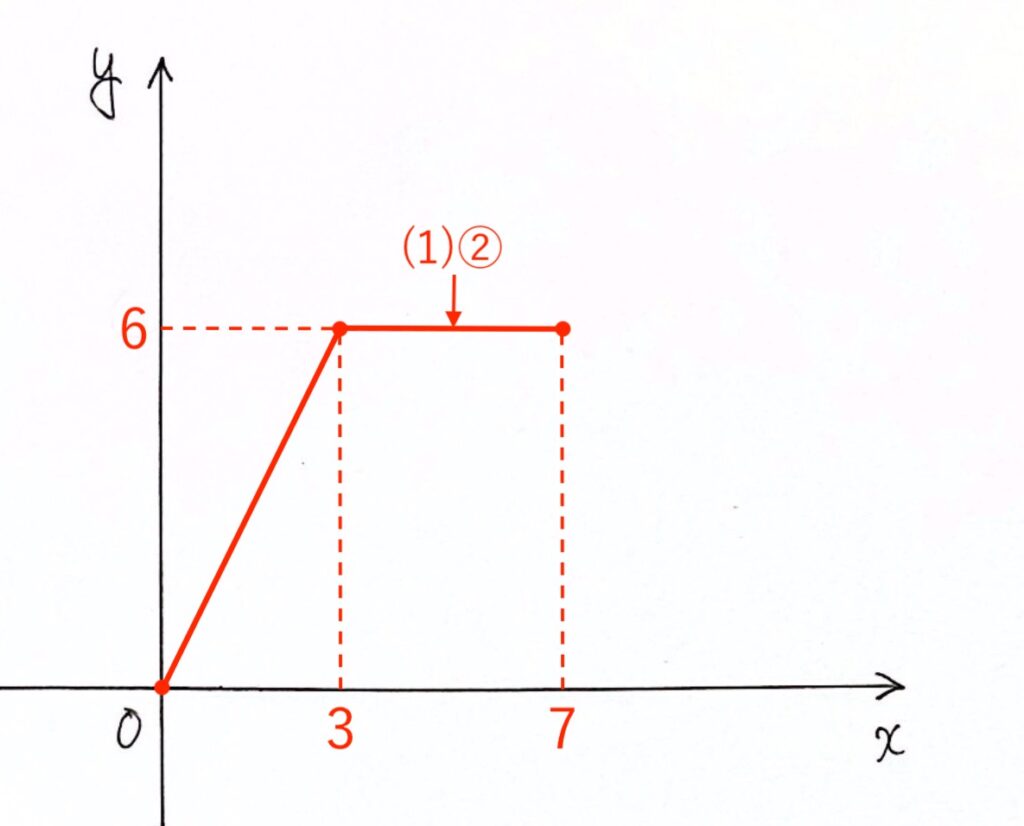
②$y = 6$($3 ≦ x ≦ 7$のとき)
$y$ の値が $6$ で一定の、真横に伸びる直線。
点(3, 6) から 点(7, 6) まで直線で結びます。
③$y = -2x+20$($7 ≦ x ≦ 10$のとき)
ここもコツがいります。
$y = -2x+20$ は、もちろん
- 傾き:$-2$
- 切片:$20$
の直線ですが、
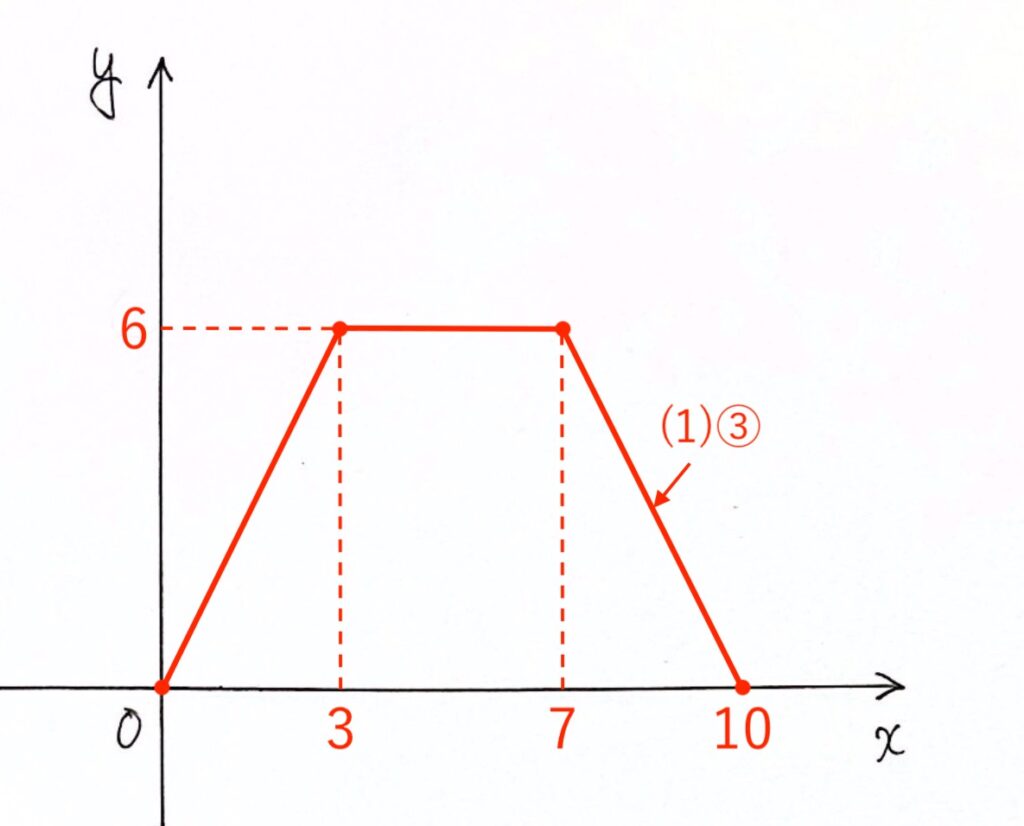
定義域が $7 ≦ x ≦ 10$ なので、これだけではグラフがうまく描けません。
そこで、$y=0$ を代入すると、
$0=-2x+20$
$2x=20$
$x=10$
となり、点(10, 0) を通ることが分かります。
なので、点(7, 6) から点(10, 0)まで直線で結べばOK。
これでグラフは完成です。
以上より、問題(2) の解答は以下のようになります。
【まとめ】「動く点P」の解き方
動く点Pの問題は、とにもかくにも
図を描く
という鉄則を守りましょう。
図を描いてから、三角形の面積を考えていくことが大切です。
質問・要望があれば気軽にコメントください👍
参考:「動く点P」の解き方【裏ワザ】
ここまで、動く点Pの問題の解き方を見てきましたが、けっこう大変だな〜と思いませんでしたか?
実は、教科書に載っていない「裏ワザ」の方が簡単に&早く解けてしまいます。
一次関数の「動く点P」の問題がはっきり言って苦手だ どうやって解いたらいいのか分からない、時間がすごくかかってしまう グラフの描き方もイマイチ自信がない・・・ こんな悩みをお持ちの人でも、今回の記事を読めばスッキリ解消します。[…]
参考:「動く点P、Q(2つ)」の解き方【王道】
なお、動く点P、Q(2つ)の問題「二次関数 $y=ax^2$」はこちら。
動く点がP、Qの2つある問題がよくわからない・・・ 動く点が2つあるとき 関数 y = ax² のグラフがうまく描けない! 学校や塾よりもわかりやすく教えてほしい! こういった要望に応えます。 この記[…]