【中学数学】比例のグラフがスッキリ理解！【比例定数・傾き・変化の割合はカンタン】

比例のグラフのかき方、読み取り方がよくわからない

比例定数って何なのかイマイチわからない

直線の傾き、変化の割合と言われてもピンと来ない

こういった悩みを持っている人に向けて、この記事を書きました。

「比例とは何か？」から始まり「比例のグラフのかき方・読み方」まで、わかりやすく説明していきます。

この記事を読めば、比例の関係をスッキリ理解できるようになります。

比例とは？

「比例」とは、教科書的に言えば「xの値が2倍, 3倍, ・・・になるとき、yの値も2倍, 3倍, ・・・になる」ことです。

例えば、「$1$本$100$円のペンがあって、$x$本買ったら合計 $y$円になる」みたいな問題ですね。

この場合、$x$と$y$の関係式は「$y = 100x$」ですが、この「$100$」のことを比例定数と言います。

【比例の関係】比例定数とは？

学校の授業では、比例の関係における「比例定数」はこう習いました。

例えば、

・$y = 2x$ → 比例定数は $2$

・$y = x$ → 比例定数は $1$

・$y = -3x$ → 比例定数は $-3$

・$\displaystyle{ y = {1 \over 2}x } $ → 比例定数は $\displaystyle{ {1 \over 2} } $

という具合です。

ちなみに、この「比例定数」は別名「傾き」とか「変化の割合」とも言います。

後々習うので、ここで覚えておきましょう。

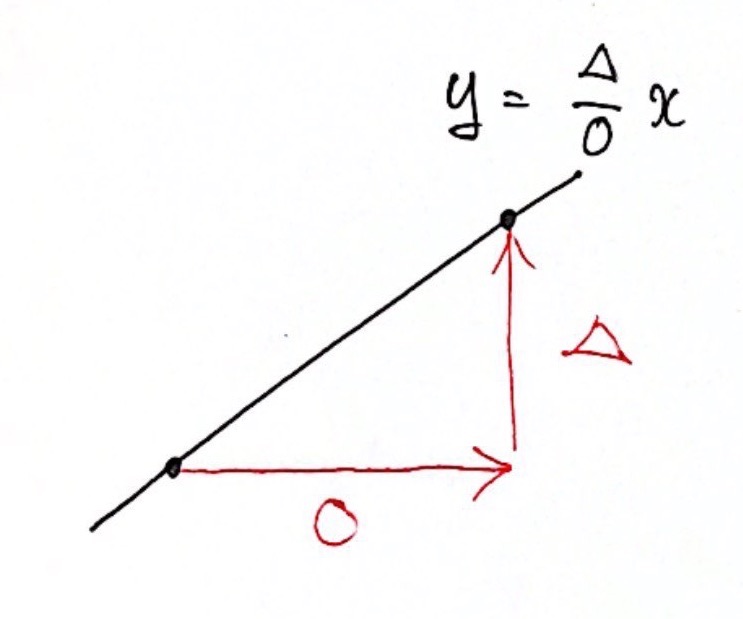
比例定数（傾き）は「グラフの進み方」

比例の関係における「比例定数（傾き）」は簡単に言うと「グラフの進み方」です。

注意点1：

注意点2：

いくつか例を挙げて説明します。

【例1】$y = x$

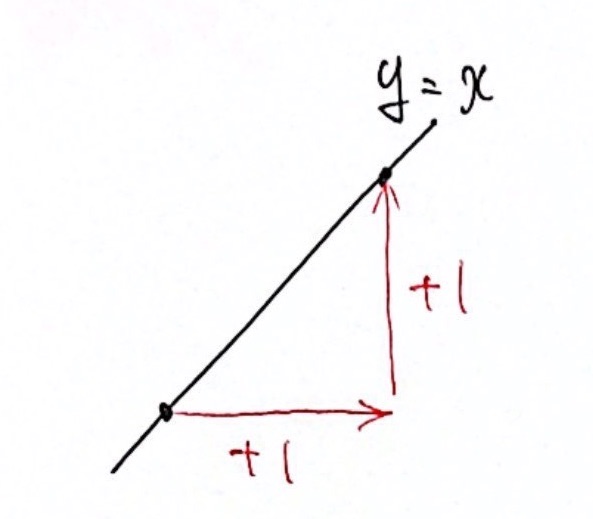
右に 1 進んで、上に 1 進む

→ 比例定数（傾き）は $\displaystyle{ \color{red}{1} \over \color{red}{1} } = 1 $

【例2】$y = 2x$

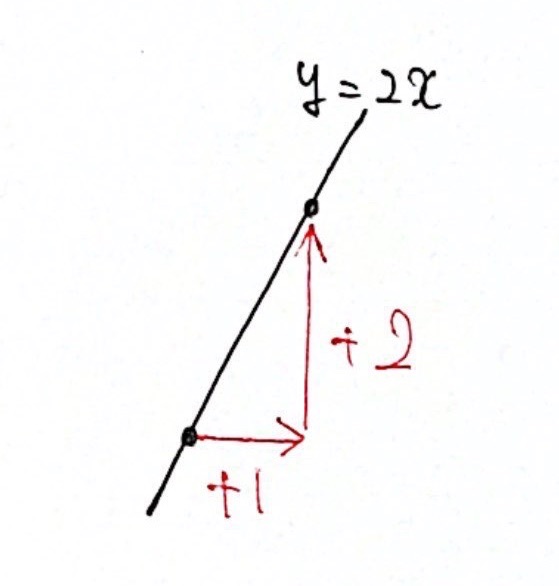
右に 1 進んで、上に 2 進む

→ 比例定数（傾き）は $\displaystyle{ \color{red}{2} \over \color{red}{1} } = 2 $

【例3】$\displaystyle{ y = {1 \over 2} x } $

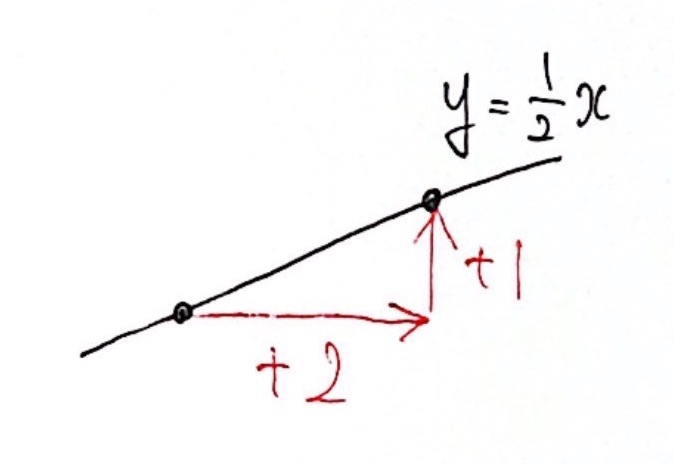
分数になっても考え方は同じ。

右に 2 進んで、上に 1 進む

→ 比例定数（傾き）は $\displaystyle{ \color{red}{1} \over \color{red}{2} } $

【例4】$y = -x$

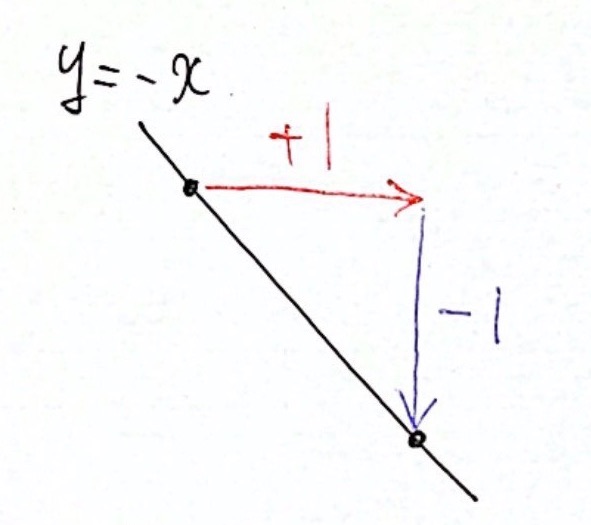
右に 1 進んで、下に 1 進む

→ 比例定数（傾き）は $\displaystyle{ \color{blue}{−1} \over \color{red}{1} } = −1 $

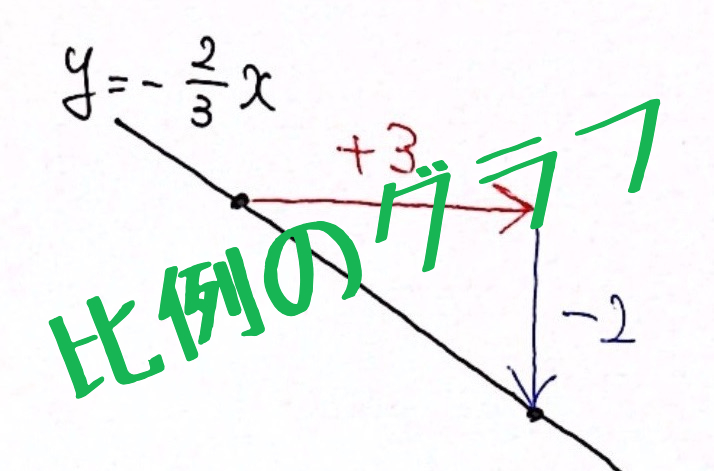
【例5】$\displaystyle{ y = −{2 \over 3}x } $

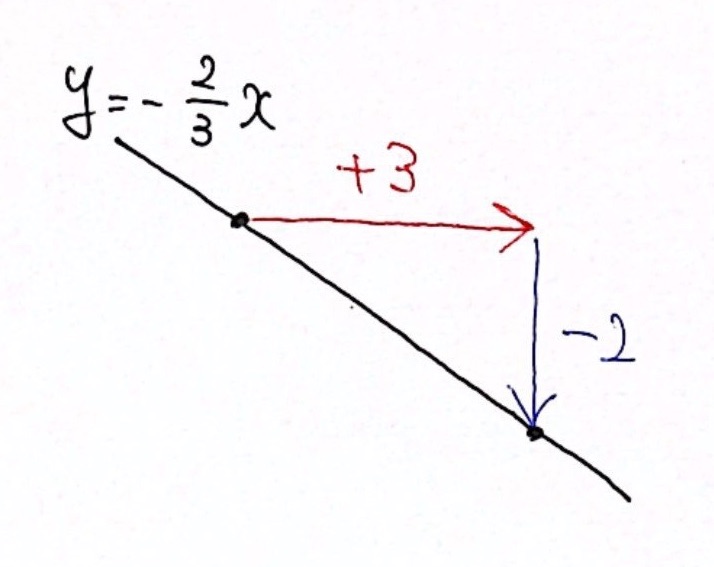
右に 3  進んで、下に 2 進む

→ 比例定数（傾き）は $\displaystyle{ { \color{blue}{−2} \over \color{red}{3} } = −{2 \over 3} } $

比例のグラフを「描く」問題

では、実際に比例のグラフを描いてみましょう。

比例のグラフを描くときは、「原点Oを通る直線」であることを忘れずに！

【例題1-1】$y = 3x$ のグラフをかけ。

比例定数は $\displaystyle{ 3= { \color{red}{3} \over \color{red}{1} } }$

→ 右に 1 進んで、上に 3 進む直線

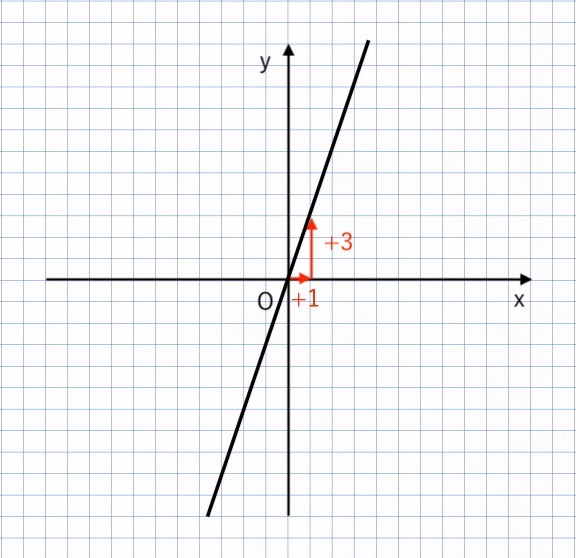
【例題1-2】$y = -2x$ のグラフをかけ。

比例定数は $\displaystyle{ −2 = {\color{blue}{−2} \over \color{red}{1} } }$

→ 右に 1 進んで、下に 2 進む直線

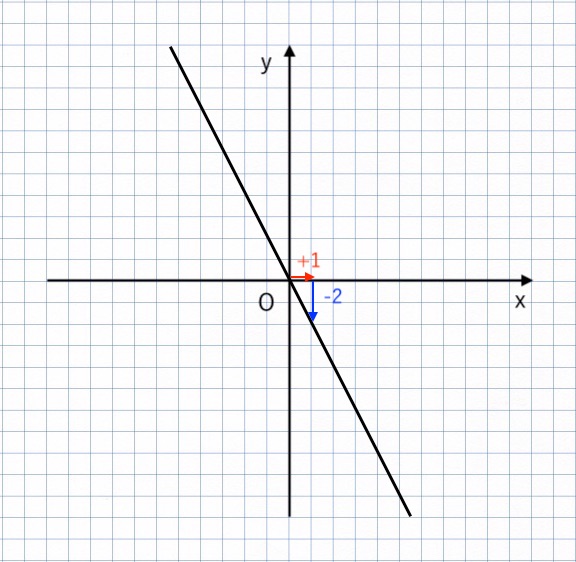
【例題1-3】$\displaystyle{y = {2 \over 3} x}$ のグラフをかけ。

比例定数は $\displaystyle{ \color{red}{2} \over \color{red}{3} }$

→ 右に 3 進んで、上に 2 進む直線

比例のグラフを「読む」問題

では、今度は比例のグラフを読み取ってみましょう。

グラフを読み取って「xとyの関係を式で表す」問題です。

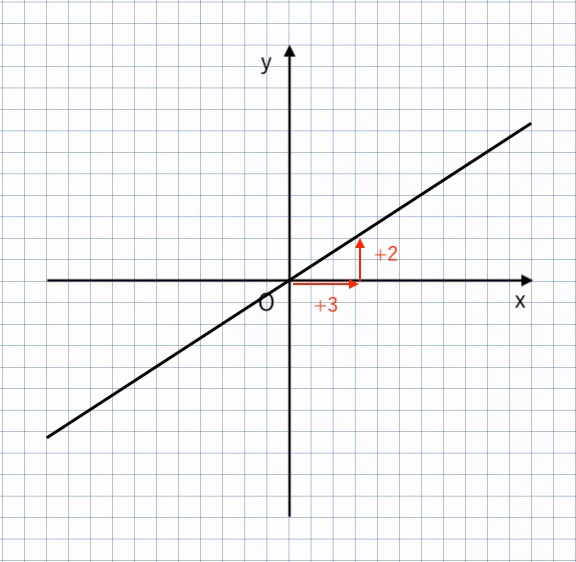
【例題2-1】

右に 1 進んで、上に 2 進んでいるので、

比例定数（傾き）は $\displaystyle{ {\color{red}{2} \over \color{red}{1} } = 2 } $

よって、$y = 2x$

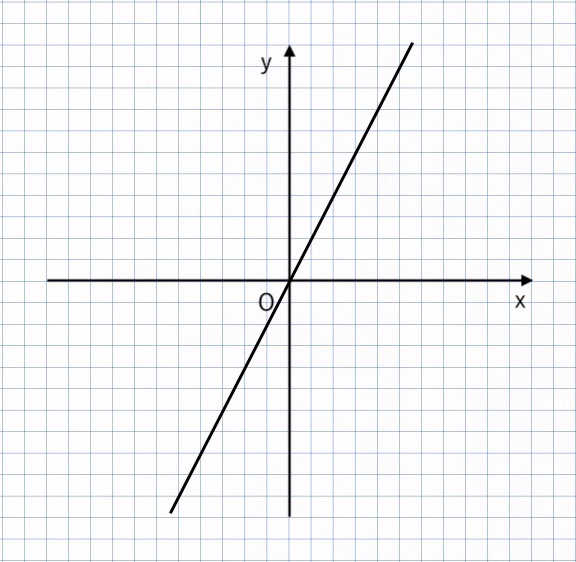
【例題2-2】

右に 3 進んで、上に 2 進んでいるので、

比例定数（傾き）は $\displaystyle{ { \color{red}{2 } \over \color{red}{3} } } $

よって、$\displaystyle{ y = {2 \over 3} x} $

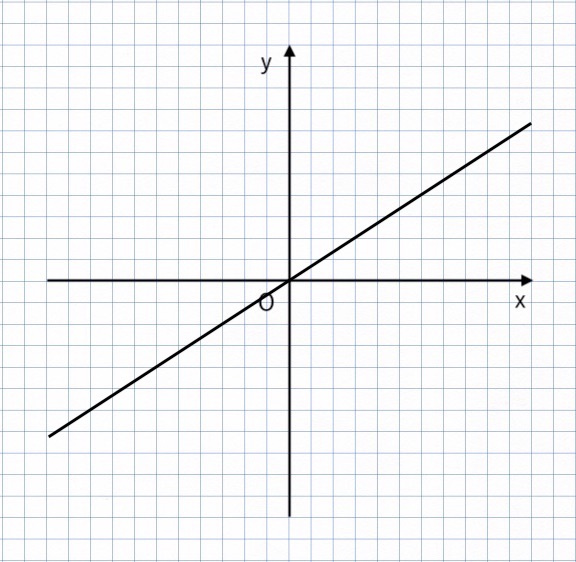
【例題2-3】

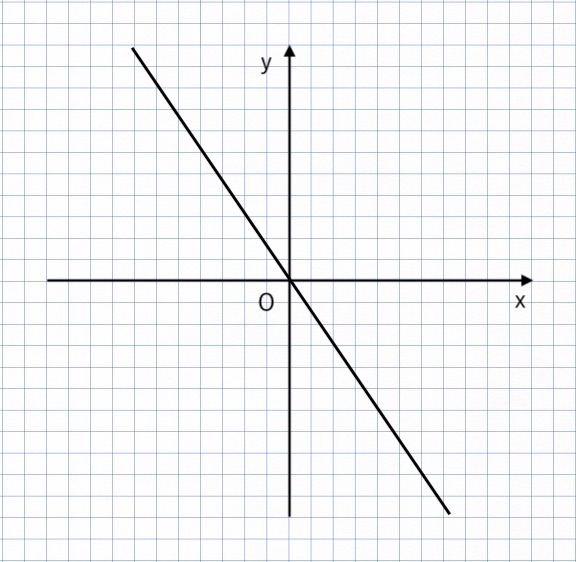
右に 2 進んで、下に 3 進んでいるので、

比例定数（傾き）は $\displaystyle{ { \color{red}{−3} \over \color{red}{2} } = −{3 \over 2 } } $

よって、$\displaystyle{ y = −{3 \over 2 }x } $

参考：「比例」と「比」の関係

実は「比例」と「比」は繋がっています。

簡単に言えば、「比例」とは「比が変わらない（一定である）こと」です。

初めに挙げた例「$1$本$100$円のペンがあって、$x$本買ったら合計 $y$円になる」で言えば、

という比がずーっと成り立ちます。

ペン$1$本で $100$円

ペン$2$本で $200$円

ペン$3$本で $300$円

・

・

・

ペン $x$本で $y$円

ここで、

という比例式を解くと

が求まります。

このように「比例の問題」は「比」を使っても解くことができます。

似たような比例の問題をマスターしたい人はこちら。

準備中

質問・要望があれば気軽にコメントください👍