【中2数学】１次関数 y = ax + b の変域の求め方をわかりやすく解説！【テストによく出る問題つき】

１次関数 y = ax + b の変域の求め方がよく分からない！

いつも yの変域を間違えて答えちゃうんだけど、なんでだろう？

どうやって解いたら １次関数 y = ax + b の変域がちゃんと出るの？

こういった疑問に答えます。

このページを読めば、例えば

のような「１次関数 y = ax + b の変域を求める問題」がスラスラ解けるようになります。

１次関数 y = ax + b のグラフ

１次関数 y = ax + b のグラフ のおさらいです。

１次関数 y = ax + b  は

$ \begin{cases}
傾き a \\
\\
切片 b \\
\end{cases}$

の直線です。

傾き a

１次関数における「傾き（変化の割合）」は簡単に言うと「グラフの進み方」です。

Point：傾き a の符号（プラス・マイナス）によって、グラフの進み方（右上がり・右下がり）が変わる

✔︎ a＞0（プラス）のとき

右上がりの直線

例：$\displaystyle{ y = \color{red}{ 3 \over 2 }x + 1 }$

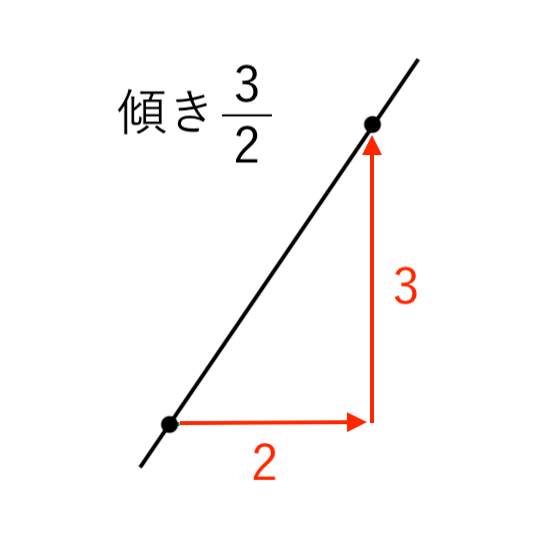
• 右に「$\color{red}{2}$」進んで
• 上に「$\color{red}{3}$」進む

→ 傾きは $ \displaystyle{ \color{red}{3} \over \color{red}{2} } $

✔︎ a＜0（マイナス）のとき

右下がりの直線

例：$\displaystyle{ y = \color{blue}{ −{ 3 \over 2 } }x + 1 }$

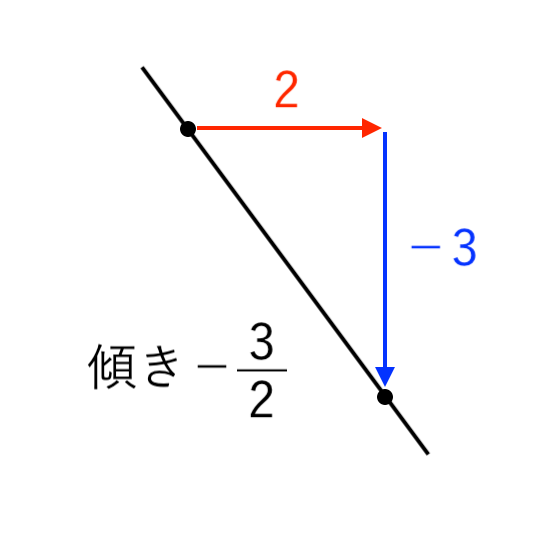
• 右に「$\color{red}{2}$」進んで
• 下に「$\color{blue}{−3}$」進む

→ 傾きは $ \displaystyle{ {\color{blue}{−3} \over \color{red}{2} } = −{3 \over 2} } $

切片 b

「切片」は、「グラフと $y$ 軸との交点の $y$ 座標」のことを言います。

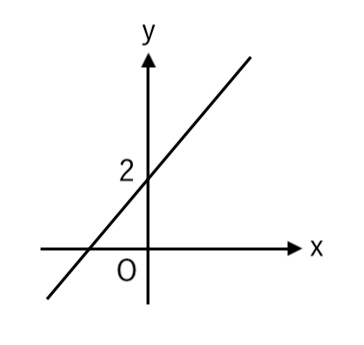
例えば、ある直線が $y$ 軸と 点$(0,2)$ で交わっている場合

切片は「$2$」になります。

１次関数のグラフの書き方

１次関数のグラフの書き方（手順）は、以下の通り。

例えば、１次関数 $\displaystyle{ y = { 3 \over 2 }x − 5 }$ のグラフを書いてみましょう。

① 切片をとる

切片は $− 5 $ なので、$y$ 軸と点$(0, −5)$ で交わる。

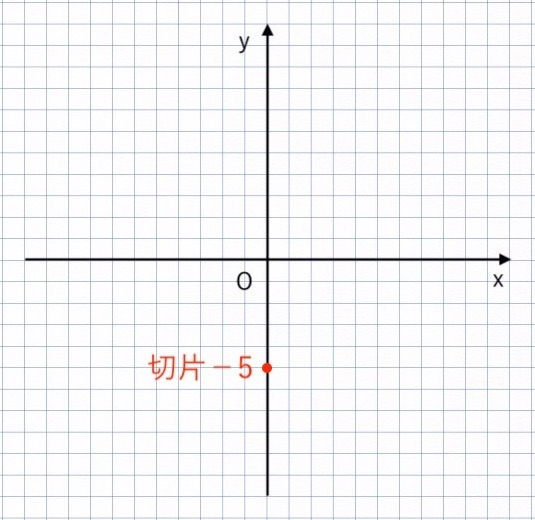
② 傾きをとる

傾きは $ \displaystyle{ \color{red}{3} \over \color{red}{2} } $ なので

• 右に「$\color{red}{2}$」進んで
• 上に「$\color{red}{3}$」進む

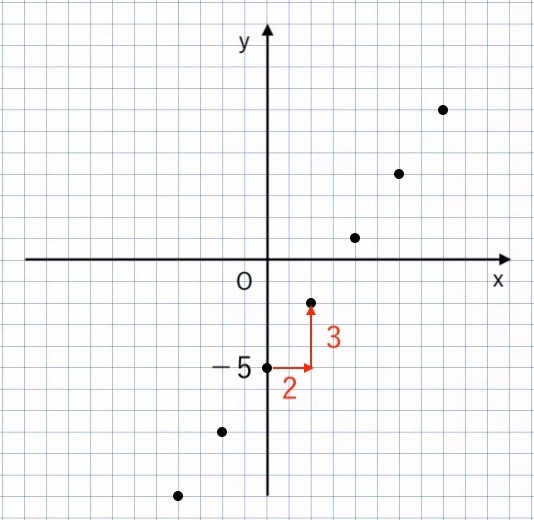
③ 直線をひく

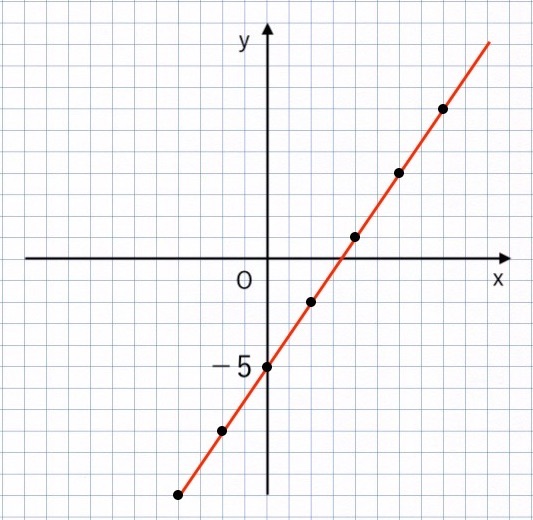
これで１次関数のグラフが完成です。

変域（へんいき）とは？

変域（へんいき）とは、ひとことで言えば「変数（ $\color{red}{x, y}$ など）が動く範囲」のことです。

【例1】$x$ の変域が $−1≦x≦2$

「$−1≦x≦2$」は「$x$は $−1$以上 $2$以下」という意味で、

数直線（$x$軸）で表すと

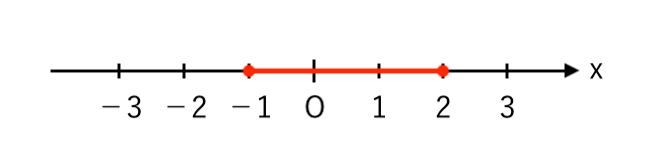
$x$は赤色の部分しか動けないということ。

【例2】$y$ の変域が $0≦y≦4$

「$0≦y≦4$」は「$y$は $0$以上 $4$以下」という意味で、

数直線（$y$軸）で表すと

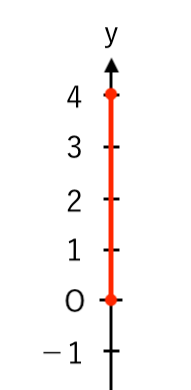
$y$は赤色の部分しか動けないということ。

１次関数 y = ax + b の変域の求め方【ポイント】

「１次関数 y = ax + b の変域の求め方」のポイントは

$ $　簡単なグラフをかく

ということです。

【例3】１次関数 $y=2x − 3$ について、$x$ の変域が $−3≦x≦5$ のときの $y$ の変域は？

具体的な解き方を説明します。

① １次関数のグラフを点線でかく

② $x$ の変域「$−3≦x≦5$」を $x$軸にとる

③ $x$ の範囲をグラフにとる

④ 高さ（$y$座標）が最大・最小の点を読み取る

⑤ $y$ の変域は「$ \color{blue}{−9}≦y≦\color{red}{7} $」

こんな感じでグラフをかくと、正しい答えが導けます。

１次関数 y = ax + b の変域の求め方【練習問題】

１次関数 y = ax + b の変域の求め方 が分かったところで、学校のテストや高校入試でよく出るパターンの問題も解いてみましょう。

【問題1】２次関数 $ y = −2x + 5 $ について、$x$ の変域が $−2≦x≦4$ のときの $y$ の変域を求めなさい。

実際に簡単なグラフをかいて、高さ（$y$座標）が最大・最小の点を読み取ってみましょう。

【解答・解説】を見る

【解答】$ −3≦y≦9 $

【解説】

簡単なグラフをかくと

高さが最大・最小の点を読み取ると

$ $　$ \color{blue}{−3}≦y≦\color{red}{9} $

【問題2】１次関数 $ y = −2x + b \enspace (−1≦x≦2)$ について、$y$ の最小値が $−1$ のとき、定数 $b$ の値を求めなさい。

傾きが $−2$ より、右下がりの直線であることをヒントに解いていきます。

【解答・解説】を見る

【解答】$ b = 3 $

【解答】

簡単なグラフをかくと

右下がりの直線なので、$x=2$ のとき 最小値 $y = \color{blue}{−1} $ をとります。

つまり、点$(2, \color{blue}{−1} )$ を通るということです。

$ y = −2x + b$ に代入すると

$ −1 = −2×2 + b$

$ b = 3 $

【問題3】$a$ が負の数である１次関数 $ y = ax + 3 $ について、$x$ の変域が $−1≦x≦2$ のとき、$y$ の変域は $−1≦x≦5$ であった。このとき、$a$ の値を求めなさい。

【解答・解説】を見る

【解答】$ a = −2$

【解説】

傾き $a$ が負の数なので、右下がりの直線。

よって、2点$(−1, 5)$、$(2, −1)$ を通ります。

簡単なグラフをかくと

$ y = ax + 3 $ に 点$(−1, 5)$ を代入すると

$ 5 =− a + 3 $

$ a = −2$（負の数より適する）

【問題4】2点 $A(1, 7)$, $B(6, -2)$ がある。１次関数 $ y = ax + 2 $ と線分$AB$が共有する点を持つように、$a$ の値の範囲を求めなさい。

最後は変域の問題ではないですが、テストによく出るパターンの問題 なのでやっておきましょう。

【解答・解説】を見る

【解答】$ \displaystyle{ − {2 \over 3}≦a≦5 }$

【解説】

１次関数 $ y = ax + 2 $ は、傾き $a$、切片 $2$ の直線。

これと線分$AB$が共有する点を持つときというのは、例えば

こんな感じです。

なので、傾き $a$ が「最大になるとき」と「最小になるとき」の2つに分けて考えます。

 

$ $[1] 傾き $a$ が 最大になるのは 点$A(1, 7)$ を通るとき。

$ y = ax + 2 $ に $A(1, 7)$ を代入して

$ $　$ 7 = a + 2 $

$ $　$ a = 5 $

 

$ $[2] 傾き $a$ が 最小になるのは 点$B(6, −2)$ を通るとき。

$ y = ax + 2 $ に $B(6, −2)$ を代入して

$ $　$ −2 = 6a + 2 $

$ $　$ \displaystyle{ a = − {2 \over 3} }$

 

$ $[1]、[2] より

$ $　$ \displaystyle{ − {2 \over 3}≦a≦5 }$

以上です。お疲れ様でした！

最後に

最後にまとめです。

「１次関数 y = ax + b の変域の求め方」のポイントは

$ $　簡単なグラフをかく

ということ。

今回紹介した問題は、学校のテストや高校入試でもよく出るパターンばかりです。

しっかり復習しておきましょう！

比例のグラフの傾き（変化の割合）

１次関数の傾き（変化の割合）は、比例のグラフと同じ考え方ですね。

関連記事

【中学数学】比例のグラフがスッキリ理解！【比例定数・傾き・変化の割合はカンタン】

比例のグラフのかき方、読み取り方がよくわからない 比例定数って何なのかイマイチわからない 直線の傾き、変化の割合と言われてもピンと来ない こういった悩みを持っている人に向けて、この記事を書きました。 「比例とは何か？」から始[…]

質問・要望があれば気軽にコメントください👍