【三角比の相互関係】公式を使わずサクッと簡単にsin cos tanを求める裏ワザ【注意点あり】

2022年9月7日
数学I

数学I

【三角比の相互関係】公式を使わずサクッと簡単にsin cos tanを求める裏ワザ【注意点あり】

sin cos tanを求めるときに「三角比の相互関係」の公式をいちいち使うのが面倒だ・・・

「三角比の相互関係」の公式3つを使わずに、サクッと簡単に計算する方法が知りたい！

こういった要望に応えます。

「三角比の相互関係」の公式は、三角比や図形の問題を解く上で必ず覚えておかなければいけません。

$\sin^2 \theta + \cos^2 \theta = 1$
$\displaystyle { \tan \theta = {\sin \theta \over \cos \theta} }$
$\displaystyle { 1 + \tan^2 \theta = {1 \over \cos^2 \theta} } $

とはいえ、3つの公式をしっかり暗記した上で使い分ける必要があったり、2乗の計算が入っていたりと、少し面倒なのも事実です。

そこで、今回は「三角比の相互関係」の公式を使わず、サクッと簡単にsin cos tanを求める「裏ワザ」を教えます。

この裏ワザを使いこなすことによって、ライバルたちが公式でせっせと計算している中、あなたは 一瞬で＆簡単に答えを出せる ようになります。

裏ワザを使う際の 注意点 もあるので、ぜひ最後まで読んでください。

1 「三角比の相互関係」の公式なしで簡単にsin cos tanを求める裏ワザ【3ステップ】
2 「三角比の相互関係」を簡単に出す裏ワザ【使い方】
3 「三角比の相互関係」を簡単に出す裏ワザ【練習問題】
4 「三角比の相互関係」を簡単に出す裏ワザ【注意点】
5 「三角比の相互関係」公式3つの覚え方・使い方

「三角比の相互関係」の公式なしで簡単にsin cos tanを求める裏ワザ【3ステップ】

「三角比の相互関係」の公式を使わず、サクッと簡単に求める 裏ワザ を教えます。

この裏ワザのポイントは

　値と符号を分けて考える

ということです。

「三角比の相互関係」を簡単に出す裏ワザは、以下の 3ステップです。

直角三角形をかいて値を求める
単位円をかいて符号を求める
値と符号を合わせる

これで完了です。

※① 直角三角形のかき方

三角比の定義より

$ \begin{cases}
\displaystyle { \sin \theta = { たて \over 斜辺 } } \\
\\
\displaystyle { \cos \theta = { よこ \over 斜辺 } } \\
\\
\displaystyle { \tan \theta = { たて \over よこ } }
\end{cases}$

となるように図をかきましょう。

「三角比の相互関係」を簡単に出す裏ワザ【使い方】

「三角比の相互関係」をサクッと簡単に出す裏ワザの使い方を見てみましょう。

【例題】$ \displaystyle { \sin \theta = { 1 \over 3 } \left( 0^\circ ＜\theta＜90^\circ \right) }$ のとき、$\cos \theta$、$\tan \theta$の値を求めよ。

①直角三角形をかいて「値」を求める

$\displaystyle { \sin \theta = { たて \over 斜辺 } = { 1 \over 3 } } $ となるような直角三角形をかきます。

（長さのバランスは適当でOK）

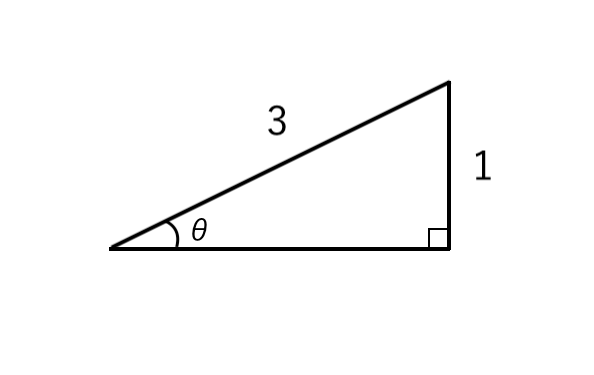
三平方の定理より、残りの1辺を出します。

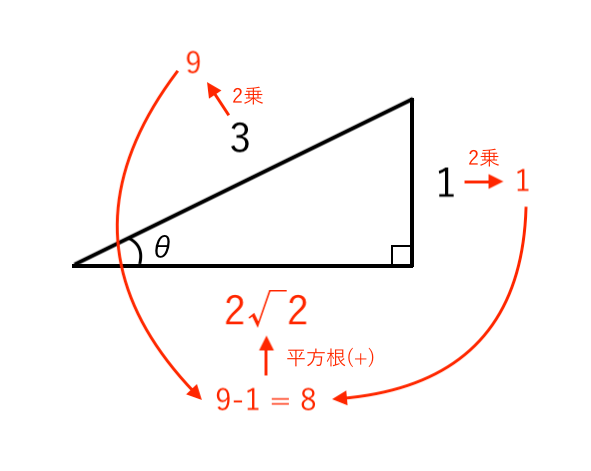
三角比の定義より、とりあえず「値」だけ求めます。

（いったん符号は無視する）

$ \begin{cases}
\displaystyle { \cos \theta = { よこ \over 斜辺 } = { 2 \sqrt{2} \over 3 } } \\
\\
\displaystyle { \tan \theta = { たて \over よこ } = { 1 \over 2 \sqrt{2} } } \\
\end{cases}$

②単位円をかいて「符号」を求める

「$0＜\theta＜90^\circ$ かつ $\sin \theta＞0（+）$」すなわち

「$0＜\theta＜90^\circ$」より

$\cos \theta$ と $\tan \theta$ の「符号」を単位円で確認すると

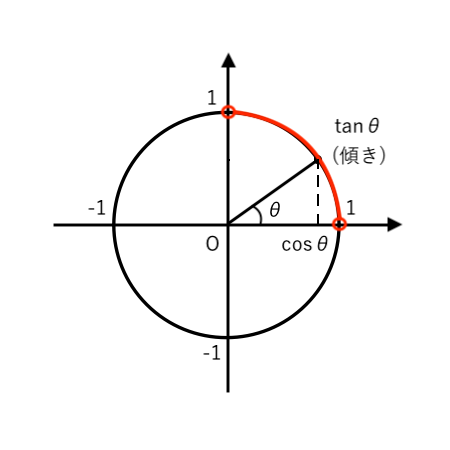
$ \begin{cases}
\cos \theta ＞0（+） \\
\\
\tan \theta ＞0（+） \\
\end{cases}$

と分かります。

このステップは、慣れてきたら頭の中でイメージするだけでOK！

③値と符号を合わせる

ステップ①「値」は

$ \begin{cases}
\displaystyle { \cos \theta = { 2 \sqrt{2} \over 3 } } \\
\\
\displaystyle { \tan \theta = { 1 \over 2 \sqrt{2} } } \\
\end{cases}$

ステップ②「符号」は

$ \begin{cases}
\cos \theta ＞0（+） \\
\\
\tan \theta ＞0（+） \\
\end{cases}$

これらを合わせて考えると

【解答】$\displaystyle { \cos \theta = { 2 \sqrt{2} \over 3 } } $, $\displaystyle { \tan \theta = { 1 \over 2 \sqrt{2} } } $

となります。

どうでしたか？ふつうに公式を使って解くよりも、かなり早く求められたのではないでしょうか。

やり方に慣れてくると大幅にスピードアップできるので、ぜひ自分のモノにしましょう！

「三角比の相互関係」を簡単に出す裏ワザ【練習問題】

色んなパターンの問題を解いて「三角比の相互関係」の裏ワザに慣れておきましょう！

【問題】三角比の1つが次の値をとるとき、他の2つの三角比の値を求めよ。

(1) $ \displaystyle { \cos \theta = { 2 \over 3 } \left( 0^\circ ＜\theta＜90^\circ \right) }$

(2) $ \displaystyle { \tan \theta = \sqrt{2} \left( 0^\circ ＜\theta＜90^\circ \right) }$

(3) $ \displaystyle { \sin \theta = { 3 \over 4 } \left( 0^\circ ＜\theta＜180^\circ \right) }$

(4) $ \displaystyle { \cos \theta = − { 2 \over \sqrt{5} } \left( 0^\circ ＜\theta＜180^\circ \right) }$

(5) $ \displaystyle { \sin \theta = − { 1 \over \sqrt{3} } \left( 0^\circ ＜\theta＜360^\circ \right) }$

(6) $ \displaystyle { \tan \theta = − {1 \over 2} \left( 0^\circ ＜\theta＜360^\circ \right) }$

え？こんなにたくさんやるの大変だって？

心配しなくても大丈夫！

先ほど伝授した「裏ワザ」を使えば一瞬で＆簡単に解けます！

(1) $ \displaystyle { \cos \theta = { 2 \over 3 } \left( 0^\circ ＜\theta＜90^\circ \right) }$

① 値

$ \displaystyle { \cos \theta = { 2 \over 3 } }$ となるような直角三角形をかくと

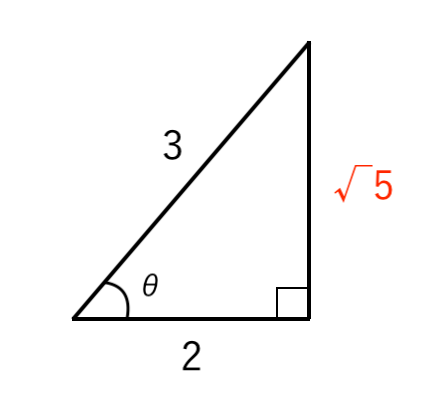
$ \begin{cases}
\displaystyle { \sin \theta = { \sqrt{5} \over 3 } } \\
\\
\displaystyle { \tan \theta = { \sqrt{5} \over 2 } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜90^\circ$ かつ $\cos \theta＞0（+）$」すなわち

「$0^\circ ＜\theta＜90^\circ$」より、単位円をかくと

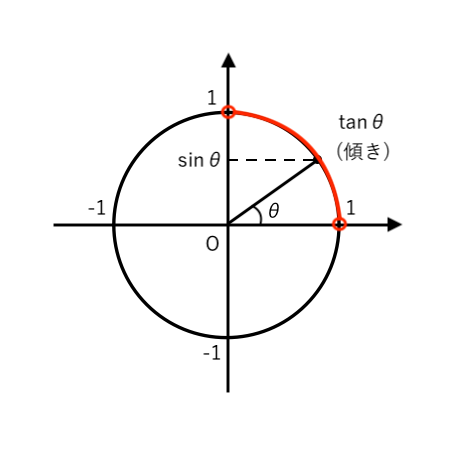
$ \begin{cases}
\sin \theta ＞0（+） \\
\\
\tan \theta ＞0（+） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \sin \theta = { \sqrt{5} \over 3 } }$, $ \displaystyle { \tan \theta = { \sqrt{5} \over 2 } }$

(2) $ \displaystyle { \tan \theta = \sqrt{2} \left( 0^\circ ＜\theta＜90^\circ \right) }$

① 値

$ \displaystyle { \tan \theta = \sqrt{2} }$ となるような直角三角形をかくと

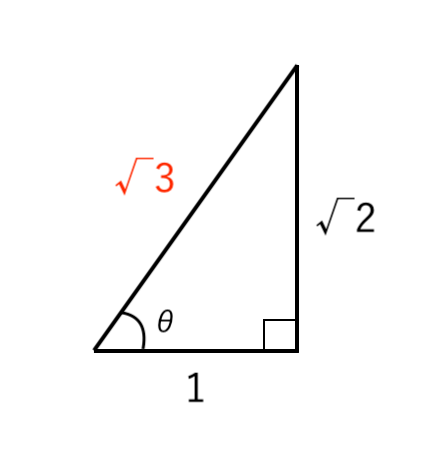
$ \begin{cases}
\displaystyle { \sin \theta = { \sqrt{2} \over \sqrt{3} } } \\
\\
\displaystyle { \cos \theta = { 1 \over \sqrt{3} } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜90^\circ$ かつ $ \tan \theta＞0（+）$」すなわち

「$0^\circ ＜\theta＜90^\circ$」より、単位円をかくと

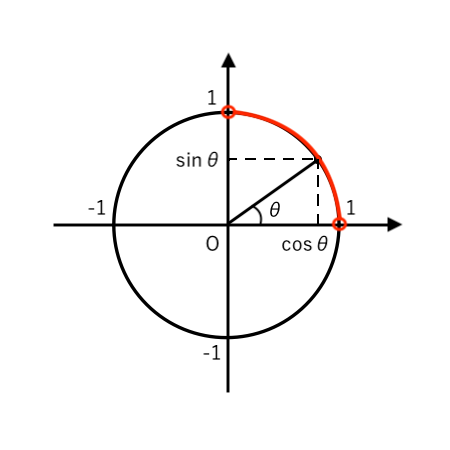
$ \begin{cases}
\sin \theta ＞0（+） \\
\\
\cos \theta ＞0（+） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \sin \theta = { \sqrt{2} \over \sqrt{3} } }$, $ \displaystyle { \cos \theta = { 1 \over \sqrt{3} } }$

(3) $ \displaystyle { \sin \theta = { 3 \over 4 } \left( 0^\circ ＜\theta＜180^\circ \right) }$

① 値

$ \displaystyle { \sin \theta = { 3 \over 4 } }$ となるような直角三角形をかくと

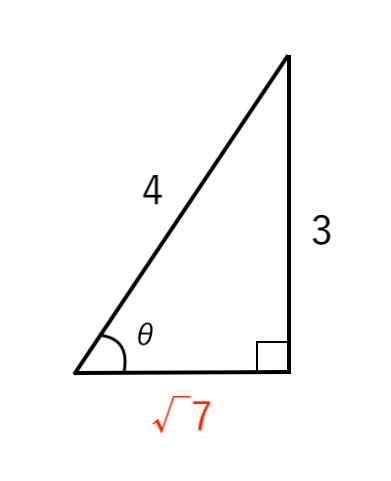
$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{7} \over 4 } } \\
\\
\displaystyle { \tan \theta = { 3 \over \sqrt{7} } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜180^\circ$ かつ $\sin \theta＞0（+）$」すなわち

「$0^\circ ＜\theta＜180^\circ$」より、単位円をかくと

$ \begin{cases}
\cos \theta ＞0（+）のとき \tan \theta ＞0（+） \\
\\
\cos \theta ＜0（−）のとき \tan \theta ＜0（−） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \cos \theta = \pm { \sqrt{7} \over 4 } }$, $ \displaystyle { \tan \theta = \pm { 3 \over \sqrt{7} } }$（複号同順）・・・（注）

（注）「複号同順」について

$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{7} \over 4 } }, \displaystyle { \tan \theta = { 3 \over \sqrt{7} } } （+と+が対応）\\
\\
\displaystyle { \cos \theta = − { \sqrt{7} \over 4 } }, \displaystyle { \tan \theta = − { 3 \over \sqrt{7} } } （−と−が対応）\\
\end{cases}$

と同じ意味。

(4) $ \displaystyle { \cos \theta = − { 2 \over \sqrt{5} } \left( 0^\circ ＜\theta＜180^\circ \right) }$

① 値

$ \displaystyle { \cos \theta = { 2 \over \sqrt{5} } } $ となるような直角三角形をかくと

（いったん符号「−」は無視する）

$ \begin{cases}
\displaystyle { \sin \theta = { 1 \over \sqrt{5} } } \\
\\
\displaystyle { \tan \theta = { 1 \over 2 } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜180^\circ$ かつ $\cos \theta ＜0（−）$」すなわち

「$90^\circ ＜\theta＜180^\circ$」より、単位円をかくと

$ \begin{cases}
\sin \theta ＞0（+） \\
\\
\tan \theta ＜0（−） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \sin \theta = { 1 \over \sqrt{5} } }$ , $ \displaystyle { \tan \theta = −{ 1 \over 2 } }$

(5) $ \displaystyle { \sin \theta = − { 1 \over \sqrt{3} } \left( 0^\circ ＜\theta＜360^\circ \right) }$

① 値

$ \displaystyle { \sin \theta = { 1 \over \sqrt{3} } } $ となるような直角三角形をかくと

（いったん符号「−」は無視する）

$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{2} \over \sqrt{3} } } \\
\\
\displaystyle { \tan \theta = { 1 \over \sqrt{2} } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜360^\circ$ かつ $\sin \theta ＜0（−）$ 」すなわち

「$180^\circ ＜\theta＜360^\circ$」より、単位円をかくと

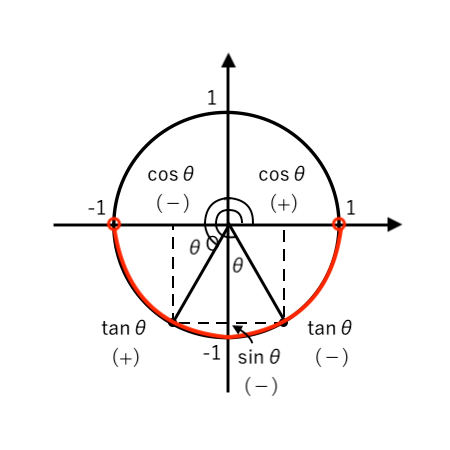
$ \begin{cases}
\cos \theta ＞0（+）のとき \tan \theta ＞0（−） \\
\\
\cos \theta ＜0（−）のとき \tan \theta ＜0（+） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \cos \theta = \pm { \sqrt{2} \over \sqrt{3} } }$ , $ \displaystyle { \tan \theta = \mp { 1 \over \sqrt{2} } }$（複号同順）・・・（注）

（注）「複号同順」について

$ \begin{cases}
\displaystyle { \cos \theta = { \sqrt{2} \over \sqrt{3} } } , \displaystyle { \tan \theta = −{ 1 \over \sqrt{2} } } （+と−が対応）\\
\\
\displaystyle { \cos \theta = − { \sqrt{2} \over \sqrt{3} } } , \displaystyle { \tan \theta = { 1 \over \sqrt{2} } } （−と+が対応）\\
\end{cases}$

と同じ意味。

(6) $ \displaystyle { \tan \theta = − {1 \over 2} \left( 0^\circ ＜\theta＜360^\circ \right) }$

① 値

$ \displaystyle { \tan \theta = {1 \over 2} } $ となるような直角三角形をかくと

（いったん符号「−」は無視する）

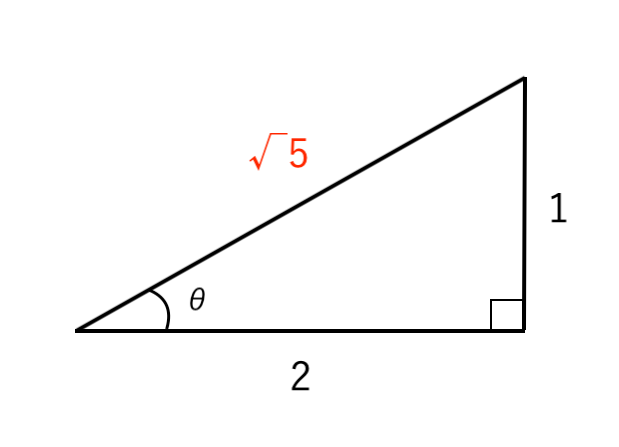
$ \begin{cases}
\displaystyle { \sin \theta = { 1 \over \sqrt{5} } } \\
\\
\displaystyle { \cos \theta = { 2 \over \sqrt{5} } } \\
\end{cases}$

② 符号

「$0^\circ ＜\theta＜360^\circ$ かつ $\tan \theta ＜0（−）$ 」すなわち

「$90^\circ ＜\theta＜180^\circ$ , $270^\circ ＜\theta＜360^\circ$」より、単位円をかくと

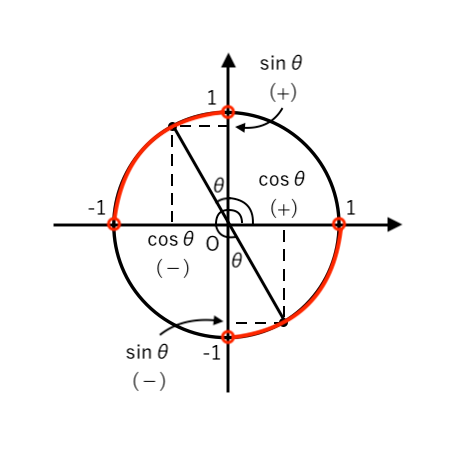
$ \begin{cases}
\sin \theta ＞0（+）のとき \cos \theta ＞0（−） \\
\\
\sin \theta ＜0（−）のとき \cos \theta ＜0（+） \\
\end{cases}$

①と②を合わせて

【解答】$ \displaystyle { \sin \theta = \pm { 1 \over \sqrt{5} } }$ , $ \displaystyle { \cos \theta = \mp { 2 \over \sqrt{5} } }$（複号同順）・・・（注）

（注）「複号同順」について

$ \begin{cases}
\displaystyle { \cos \theta = { 1 \over \sqrt{5} } } , \displaystyle { \tan \theta = −{ 2 \over \sqrt{5} } } （+と−が対応）\\
\\
\displaystyle { \cos \theta = − { 1 \over \sqrt{5} } } , \displaystyle { \tan \theta = { 2 \over \sqrt{5} } } （−と+が対応）\\
\end{cases}$

と同じ意味。