3次関数の「接線の方程式」を求めたいときは微分を使うのが基本ですが、
問題によっては、あえて 微分を使わずに 求める解き方の方がラクな場合もあります。
微分法の「接線の方程式」の求め方がイマイチ分からない 色んな解き方のパターンがあって、どれで解いたらいいのか混乱してしまう わかりやすく整理して教えてほしい! こういった要望に応えます。 高校生の中に[…]
上の記事では、ふつうに微分法で解くやり方を紹介していますが、
今回は、同じ3題を使って 微分を使わずに 「接線の方程式」を求めるやり方を解説していきます!
微分を使わない「接線の方程式」の求め方【3次関数編】
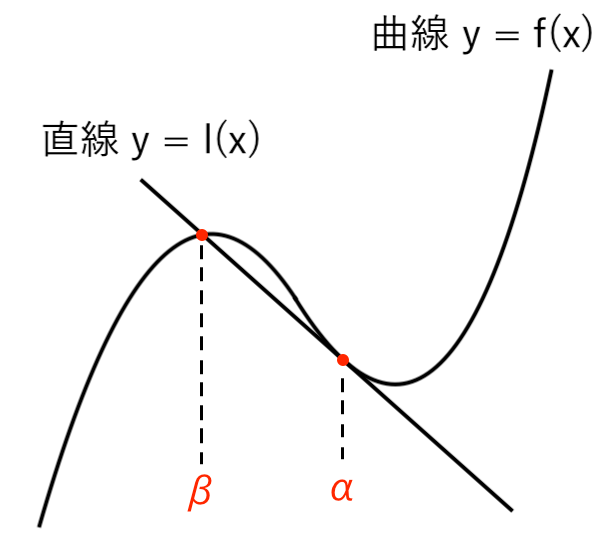
$3$ 次関数 $ f(x) =ax^3 + bx^2 +cx + d $ について
点 $( \alpha , \ f( \alpha ))$ における接線を $ l(x) = mx + n $、
接点以外の交点を $( \beta , \ f( \beta ))$ とすると
が成り立ちます。
例:3次関数と接線
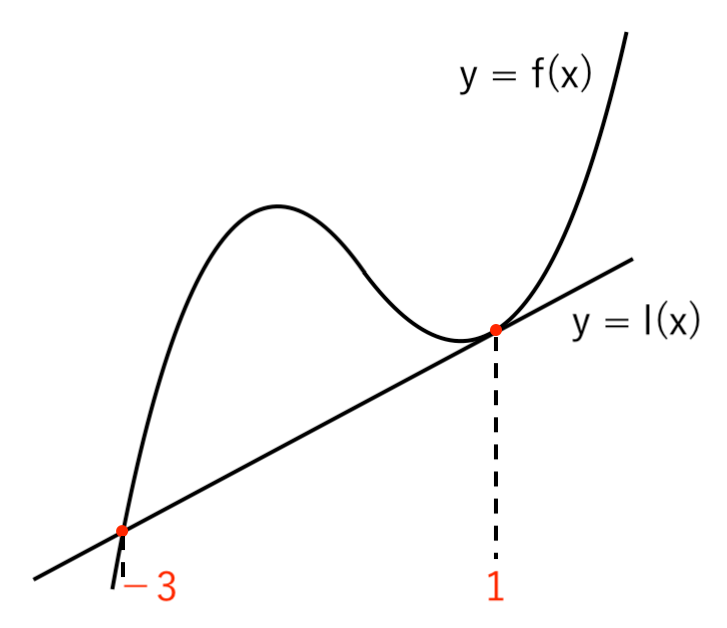
$3$ 次関数 $ f(x) = 2 x^3 + 2 x^2 −4x $
直線 $ l(x) = 6x − 6 $(接線)
を例に考えます。
$2$ 式から $ f(x), \ l(x) $ を消去すると
$ $ $ f(x) − l(x) = 2 x^3 + 2 x^2 −10x + 6 $
$ $ $ = 2 ( x^3 + x^2 −5x + 3 ) $
$ $ $ = 2 ( x−1 )( x^2 +2 x −3 ) $
$ $ $ = 2 ( x−1 )^2 ( x + 3 ) $
$ f(x) − l(x) = 0 $ とすると
$ $ $ x = −3, \ 1 \ (重解) $
確かに、$ l(x) $ は点 $ (\color{red}{1} , \ f(1)) $ における $ f(x)$ の接線で、
その接点以外の 点 $(\color{red}{−3} , \ f(−3))$ で交わっていますね。
【パターン1】接点が分かる問題(微分を使わない)
まずは「パターン1:接点が分かっている問題」を、微分を使わずに 解いてみます。
【例題1】曲線 $ y= x^3 − 5x $ 上の点 $(1, −4)$ における接線の方程式を求めよ。
【解答】
$ f(x) = x^3 − 5x $ 上の点 $(1, \ −4) $ における接線を
$ l(x) = mx + n $ とおくと
$ $ $ f(x) − l(x) = ( x−1 )^2 ( x − \alpha ) $
∴ $ x^3 − (m+5)x −n = ( x^2 −2x + 1 ) ( x − \alpha ) $
∴ $ x^3 − (m+5)x −n $ $= x^3 −(\alpha + 2)x^2 +(2 \alpha + 1 )x − \alpha $
係数を比較して
$ $ $ \begin{cases}
−(\alpha + 2) = 0 \\
\\
− (m+5) = 2 \alpha + 1 \\
\\
−n = − \alpha \\
\end{cases}$
∴ $ \begin{cases}
\alpha = − 2 \\
\\
m = −2 \\
\\
n = −2 \\
\end{cases}$
よって、求める接線の方程式は
$ $ $ y = −2x −2 $
【パターン2】傾きが分かる問題(微分を使わない)
「パターン2:傾きが分かっている問題」も、微分を使わずに 解くことができます。
【例題2】曲線 $ y= x^3 − 2x + 5 $ において、傾きが $10$ である接線の方程式を求めよ。また、そのときの接点の座標を求めよ。

【解答】
$ f(x) = x^3 − 2x + 5 $ 上の点 $(\alpha, \ f(\alpha) ) $ における接線を
$ l(x) = 10x + n $ とおくと
$ $ $ f(x) − l(x) = ( x−\alpha )^2 ( x − \beta ) $
∴ $ x^3 − 12x + 5 − n $ $= ( x^2−2 \alpha x + \alpha^2 ) ( x − \beta ) $
∴ $ x^3 − 12x + 5 − n $ $= x^3−( 2 \alpha + \beta ) x^2 + ( \alpha^2 + 2 \alpha \beta ) x − \alpha^2 \beta $
係数を比較して
$ $ $ \begin{cases}
−( 2 \alpha + \beta ) = 0 \enspace ・・・ ① \\
\\
− 12 = \alpha^2 + 2 \alpha \beta \enspace ・・・ ② \\
\\
5 − n = − \alpha^2 \beta \enspace ・・・ ③ \\
\end{cases}$
① より、$ \beta = −2 \alpha $
これと ② より、$ \alpha^2 = 4 $
∴ $ \alpha = \pm 2 $
$ $ [1] $ \alpha = 2 $ のとき
① より、$ \beta = − 4 $
③ より、$ n = −11 $
∴ 接線は $ y = 10x −11 $、接点は $(2, \ 9)$
$ $ [2] $ \alpha = − 2 $ のとき
① より、$ \beta = 4 $
③ より、$ n = 21 $
∴ 接線は $ y = 10x + 21 $、接点は $(− 2, \ 1)$
【パターン3】接点も傾きも分からない問題(微分を使わない)
最後は「パターン3:接点も傾きも分からない問題」の 微分を使わない 解き方です。
【例題3】点$(1, \ 1)$ を通り、曲線 $ y= x^3 − 4x + 5 $ に接する直線の方程式を求めよ。[12 愛媛大]
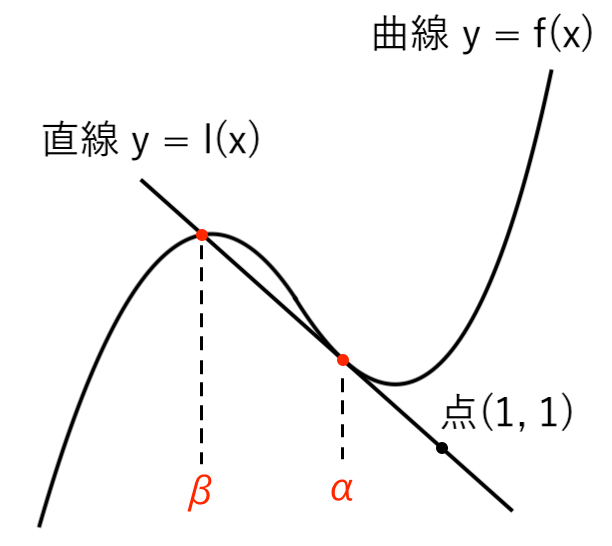
【解答】
点 $(1, \ 1) $ を通り、$ f(x) = x^3 − 4x + 5 $ に接する直線を
$ l(x) = m(x-1) + 1 $ とおくと
$ $ $ f(x) − l(x) = ( x−\alpha )^2 ( x − \beta ) $
∴ $ x^3 − (m+4)x + m + 4 $
$ $ $ = ( x^2 −2 \alpha x + \alpha^2 ) ( x − \beta ) $
$ $ $ = x^3−( 2 \alpha + \beta ) x^2 + ( \alpha^2 + 2 \alpha \beta ) x − \alpha^2 \beta $
係数を比較して
$ $ $ \begin{cases}
−( 2 \alpha + \beta ) = 0 \enspace ・・・ ① \\
\\
− (m+4) = \alpha^2 + 2 \alpha \beta \enspace ・・・ ② \\
\\
m + 4 = − \alpha^2 \beta \enspace ・・・ ③ \\
\end{cases}$
① より、$ \beta = −2 \alpha $
② より、$ m+4 = 3 \alpha^2 $
③ より、$ m+4 = 2 \alpha^3 $
∴ $ 2 \alpha^3 = 3 \alpha^2 $
∴ $ \alpha^2 ( 2 \alpha − 3 ) = 0 $
∴ $ \displaystyle{ \alpha = 0, \ {3 \over 2} } $
$ $ [1] $ \alpha = 0 $ のとき
$ $ $ \beta = 0 , \ m = −4 $
∴ 接線は $ y = −4( x −1 ) + 1 = −4x + 5 $
$ $ [2] $ \displaystyle{ \alpha = {3 \over 2} } $ のとき
$ $ $ \displaystyle{ \beta = −3 , \ m = {11 \over 4} } $
∴ 接線は $ \displaystyle{ y = {11 \over 4}( x −1 ) + 1 = {11 \over 4}x −{7 \over 4} } $
【まとめ】微分を使わない「接線の方程式」【3次関数編】
最後にまとめです。

$3$ 次関数 $ f(x) =ax^3 + bx^2 +cx + d $ について
点 $( \alpha , \ f( \alpha ))$ における接線を $ l(x) = mx + n $、
接点以外の交点を $( \beta , \ f( \beta ))$ とすると
質問・要望があれば気軽にコメントください👍