2次関数の「変化の割合」を求める計算が大変だなあ〜
難しくて計算ミスもしそうだし・・・
2次関数の「変化の割合」の簡単な求め方を教えてほしい!
こんなお悩みを解決します。
このページを読んで「2次関数の変化の割合を簡単に求める裏ワザ」を学べば、例えば
こんな問題が「5秒で」答えられるようになります。
【2次関数】変化の割合の簡単な求め方【裏ワザ】
結論から言います。
2次関数の「変化の割合」の簡単な求め方 は次の通り。
2次関数 $ y=ax^2$ について、
$x$ の値が $A$ から $B$ まで変化するときの
変化の割合 は
$ $ $a(A+B)$
これだけです。一瞬ですね!
【2次関数】変化の割合の簡単な求め方【例題】
この「裏ワザ」を実際に使ってみましょう!
変化の割合は
$ $ $ a (A+B) = 3 (-1 + 5) $
$ $ $ = 12 $
ね?簡単でしょ?
ふつうの解き方と比べると・・・
ここで、通常の「変化の割合」の求め方と比較してみましょう。
- $x$の増加量 $= 5 – (-1) = 6 $
- $y$の増加量 $= 3 × 5^2 – 3 × (-1)^2 = 72 $
なので、公式に当てはめると
$ $ $\displaystyle{ \text{変化の割合} = { y の増加量 \over x の増加量 } } $
$ $ $ \displaystyle{ = { 72 \over 6 } } $
$ $ $ = 12$
もちろん同じ答えが出てきましたが、
どっちの計算のやり方がラクかは言うまでもありませんね!
参考:【2次関数】変化の割合「裏ワザ」の証明
【証明】
参考までに証明を書いておきます。
2次関数 $ y=ax^2$ について、
$x$ の値が $A$ から $B$ まで変化するときの
変化の割合 を求めると
$ $ $ \displaystyle{ aB^2 – aA^2 \over B – A } $
$ $ $ = \displaystyle{ a (B^2 – A^2) \over B – A } $
$ $ $ = \displaystyle{ a (B+A) \require{cancel} \bcancel{ (B-A) } \over \bcancel{ B-A } } $
$ $ $ = \displaystyle{ a (B+A) } $
$ $ $ = \displaystyle{ a (A+B) } $ [終]
変化の割合とは?
そもそも 変化の割合 とは、簡単に言えば「直線の傾き」のこと。

例えば、ある直線が
- 右に「$\color{blue}{2}$」進んで
- 上に「$\color{red}{3}$」進む
ような場合、傾きは
$ $ $ \displaystyle{ \color{red}{3} \over \color{blue}{2} } $
となります。
同様に、2次関数 $ y=ax^2$ 上の2点 $ \left(A, \enspace aA^2 \right), \enspace \left(B, \enspace aB^2 \right)$ を通る直線の傾きを考えると
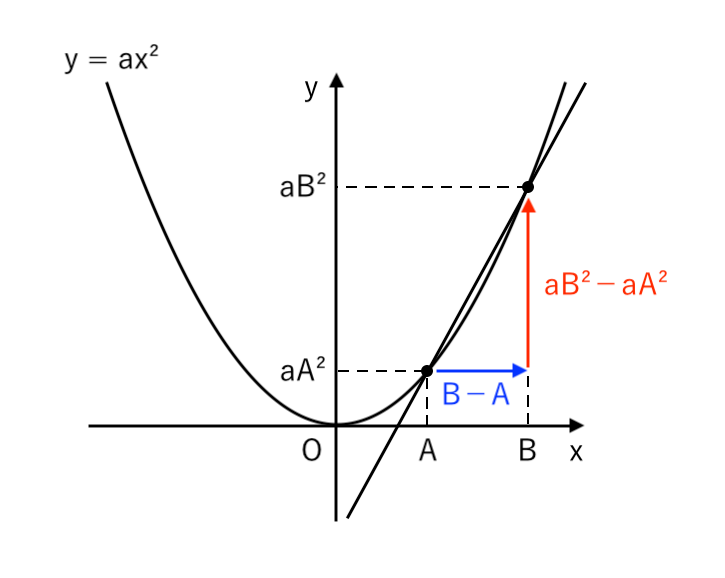
この直線は
- 右に「$\color{blue}{B−A}$」進んで
- 上に「$\color{red}{aB^2 −aA^2}$」進む
ので、傾きは
$ $ $ \displaystyle{ \color{red}{aB^2 − aA^2} \over \color{blue}{B − A} } $
と計算できるわけですね。
あとは上の証明のような流れで「$a (A+B)$」の形が求められます。
【2次関数】変化の割合の簡単な求め方【練習問題】
さっそくこの裏ワザを使って 練習問題 を解いてみましょう!
【問題】
(1)2次関数 $y=x^2$ について、$x$の値が $1$ から $3$ まで増加するときの 変化の割合を求めなさい。
(2)2次関数 $y=2x^2$ について、$x$の値が $-2$ から $1$ まで増加するときの 変化の割合を求めなさい。
(3)2次関数 $y=-x^2$ について、$x$の値が $1$ から $3$ まで増加するときの 変化の割合を求めなさい。
(4)2次関数 $y=-3x^2$ について、$x$の値が $-2$ から $0$ まで増加するときの 変化の割合を求めなさい。
(5)2次関数 $y=\displaystyle{1 \over 4} x^2$ について、$x$の値が $1$ から $3$ まで増加するときの 変化の割合を求めなさい。
(6)2次関数 $y=ax^2$ について、$x$の値が $-1$ から $3$まで増加するときの 変化の割合が $4$ のとき $a$ の値を求めなさい。
(7) $x$の値が $1$ から $3$ まで増加するとき、2つの関数 $y=ax^2$ と $y=3x+2$ の変化の割合が等しくなるような $a$ の値を求めなさい。
- 【解答・解説】を見る
-
【解答】
(1) $4$
(2) $−2 $
(3) $ −4 $
(4) $6 $
(5) $ 1 $
(6) $\displaystyle{ a = 2 } $
(7) $\displaystyle{ a = { 3 \over 4 } } $
【解説】
(1) $ 1×(1+3) = 4$
(2) $ 2(-2 + 1) = -2 $
(3) $ -1×(1 + 3) = -4 $
(4) $ -3(-2 + 0) = 6 $
(5) $\displaystyle{ { 1 \over 4} (1+3) = 1 } $
(6) $ a(-1 + 3) = 4 $ より
$ $ $ 2a = 4$
$ $ $ a = 2 $
(7) 関数 $y=3x + 2 $ の変化の割合(傾き)は $3$ で一定なので
$a(1+3) = 3$ より
$ $ $4a = 3 $
$ $ $ \displaystyle{ a = { 3 \over 4 } } $
【まとめ】2次関数「変化の割合」の簡単な求め方
最後に、2次関数の「変化の割合」の簡単な求め方(裏ワザ)のおさらいです。
2次関数 $ y=ax^2$ について、
$x$ の値が $A$ から $B$ まで変化するときの
変化の割合は
$ $ $a(A+B)$
計算が一気にスピードアップできるので、どんどん活用していきましょう!
【2次関数 y = ax²】動く点P、Q(2つ)の問題
動く点がP、Qの2つある問題がよくわからない・・・ 動く点が2つあるとき 関数 y = ax² のグラフがうまく描けない! 学校や塾よりもわかりやすく教えてほしい! こういった要望に応えます。 この記[…]
質問・要望があれば気軽にコメントください👍