【高校数学】二重根号の外し方・解き方をわかりやすく解説【一瞬で簡単に計算できる裏技】

二重根号の外し方・解き方がよくわからない

二重根号の公式が覚えにくい

二重根号に分数が入ってくる計算ができない

素早く簡単に計算する方法を知りたい

こんな悩みを持っているのなら、ぜひこの記事を読んでください。

教科書に載っているような回りくどい計算法からは、もうおさらばです。

今回は、二重根号を素早く簡単に外すやり方をわかりやすく解説します。

二重根号の計算（一般的な解き方）

二重根号とは、

のように「ルートの中にルートが入っている式」のことを言います。

よく教科書や問題集に載っている二重根号の外し方は、次のように因数分解して解く方法です。

$\sqrt{5+2\sqrt{6}}$

$=\sqrt{3+2\sqrt{3}\sqrt{2}+2}$

$=\sqrt{(\sqrt{3}+\sqrt{2})^2}$

$=\sqrt{3}+\sqrt{2}$

といった感じで、手間がかかりますよね？

ですが、実はこんな面倒臭いやり方をしなくても解けます。

今回はもっと素早く計算する方法を紹介します。

二重根号の外し方・解き方【裏技】

【例題1】二重根号の中身が 足し算（プラス）

まずは、二重根号の中身が「足し算」になっているものです。

① かけて 6、足して 5 になるような 2つの数を考える （3と2）

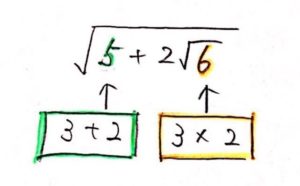
② その2つの数をルートで書く

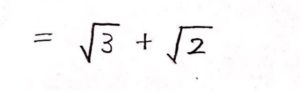
以上。

ね、簡単でしょ？

【例題2】二重根号の中身が 引き算（マイナス）

二重根号の中身が「引き算」になっている場合も、足し算のときと同様に考えますが、

マイナス（引き算）なら答えもマイナスをつけます。

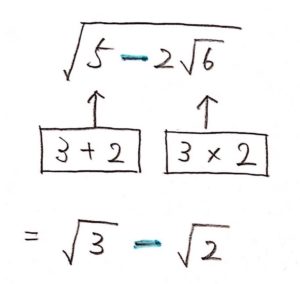
注意点（二重根号の中身が 引き算 のとき）

二重根号の中身が「引き算」のときは、書く順番に注意しましょう。

二重根号を外したら 必ずプラス（正の数）なので

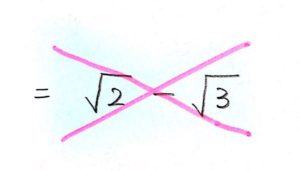
これはNG！（$\sqrt{2} ＜ \sqrt{3}$より、負の数になってしまう）

なので、二重根号を外すときは

大きい数を先に書く

ことをクセづけておきましょう。

【例題3】ルートの中身を 分数 にして解く

二重根号の中身が「$A ± $2$\sqrt{B}$」の形でないものは、無理やり 2 を作ります。

二重根号の中身を丸ごと分数にすることに注意！

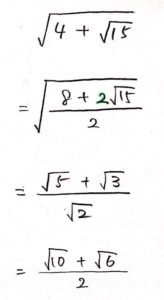
【例題4】その他

「$4\sqrt{3}$」のようなものは、2 だけ残してルートの中に入れます。

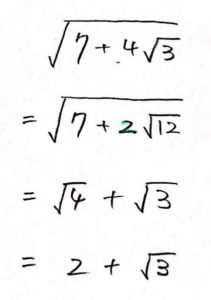
【練習問題】二重根号を外す練習をしよう！

【解答・解説】を見る

【解答】

(1) $ \sqrt{6} + \sqrt{5} $

(2) $\sqrt{7} – \sqrt{2} $

(3) $ \sqrt{7} – \sqrt{3} $

(4) $ \displaystyle { \sqrt{10} + \sqrt{6} \over 2 } $

(5) $ \displaystyle { \sqrt{30} – \sqrt{6} \over 2 } $

(6) $ 2 \sqrt{3} + 1 $

【解説】

(1) (2) 略

(3) $\sqrt{10 – \sqrt{84}}$

$= \sqrt{10 – 2 \sqrt{21}}$

$= \sqrt{7} – \sqrt{3} $

 

(4) $\sqrt{4+\sqrt{15}}$

$ = \displaystyle { \sqrt{8 + 2 \sqrt{15} \over 2 } } $

$ = \displaystyle { \sqrt{5} + \sqrt{3} \over \sqrt{2} } $

$ = \displaystyle { \sqrt{10} + \sqrt{6} \over 2 } $

 

(5) $\sqrt{9 – 3 \sqrt{5}}$

$ = \sqrt{9 – \sqrt{45} } $

$ = \displaystyle { \sqrt{18 – 2 \sqrt{45} \over 2 } } $

$ = \displaystyle { \sqrt{15} – \sqrt{3} \over \sqrt{2} } $

$ = \displaystyle { \sqrt{30} – \sqrt{6} \over 2 } $

 

(6) $\sqrt{ 9 + 4 \sqrt{4+ 2 \sqrt{3} } } $

$ = \sqrt{ 9 + 4 ( \sqrt{3} + 1 ) } $

$ = \sqrt{ 13 + 4 \sqrt{3} } $

$ = \sqrt{ 13 + 2 \sqrt{12} } $

$ = \sqrt{12} + 1 $

$ = 2 \sqrt{3} + 1 $

質問・要望があれば気軽にコメントください👍