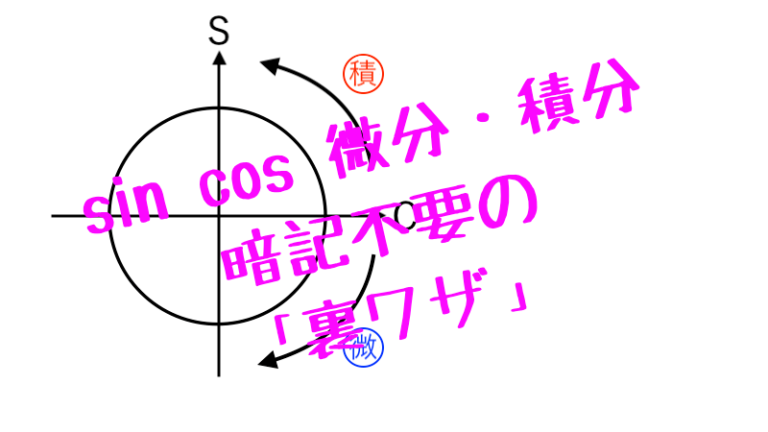
三角関数のsinとcosの微分・積分公式がややこしいな〜
符号がプラスかマイナスかいつも混乱しちゃう・・・
微積公式を暗記せずに簡単に計算する方法はないの?
こんなお悩みを解消します。
この記事を読めば、
- $ ( 2 \sin x − 3 \cos x )’ = ? $
- $ \displaystyle{ \int (−5 \cos x + \sin x) \,dx = ? } $
このような sin と cos の微分・積分が「3秒で」ミスなく計算できる ようになります。
この「裏ワザ」を 知っているか知らないかで差がつく ので、計算スピードを上げたい人はぜひ最後まで読んでみてください!
【三角関数】sinとcosの微分・積分公式
三角関数における sinとcosの微分・積分公式 って、符号がややこしいですよね?
✔︎ sinとcosの微分公式
- $ $ $ ( \sin x )’ = \cos x $
- $ $ $ ( \cos x )’ = \color{red}{−} \sin x $
- $ $ $ ( \color{red}{−} \sin x )’ = \color{red}{−} \cos x $
- $ $ $ ( \color{red}{−} \cos x )’ = \sin x $
✔︎ sinとcosの積分公式
- $ $ $ \displaystyle{ \int \sin x \,dx = \color{red}{−} \cos x + C } $
- $ $ $ \displaystyle{ \int \cos x \,dx = \sin x + C } $
- $ $ $ \displaystyle{ \int ( \color{red}{−} \sin x ) \,dx = \cos x + C } $
- $ $ $ \displaystyle{ \int ( \color{red}{−} \cos x ) \,dx = \color{red}{−} \sin x + C } $
$ $ ($C$ は積分定数)
特にマイナスがついている時の微分・積分は、符号を逆に考えないといけないので 計算ミスが起こりやすいポイント です。
ですが、安心してください。
次に紹介する「裏ワザ」を知っていたら、これらの公式は暗記する必要がありません。
sinとcos の微分・積分を「3秒で」計算する裏ワザ
三角関数の sinとcosの微分・積分 を一瞬で簡単にやる「裏ワザ」を説明します。
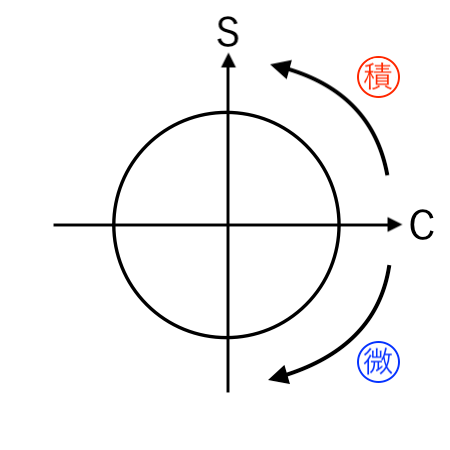
上図の見方は、次の通り。
【軸】
- 横軸:C(cos)
- 縦軸:S(sin)
【回転】
- 反時計回り(左回り) → 積分
- 時計回り(右回り) → 微分
実際の使い方を見ていきましょう。
sin の微分・積分
sin の微分:$ ( \sin x )’ = \cos x $
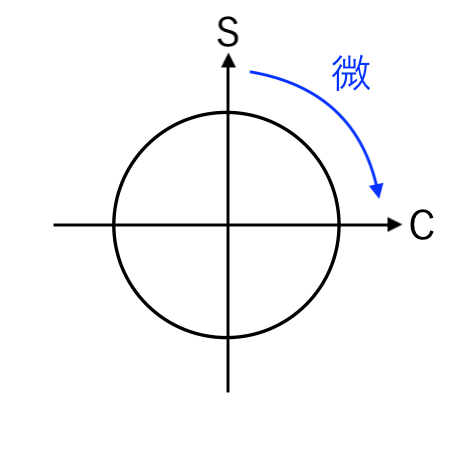
すると、
C(cos)
に移るので
となります。
sin の積分:$ \displaystyle{ \int \sin x \,dx = −\cos x + C } $
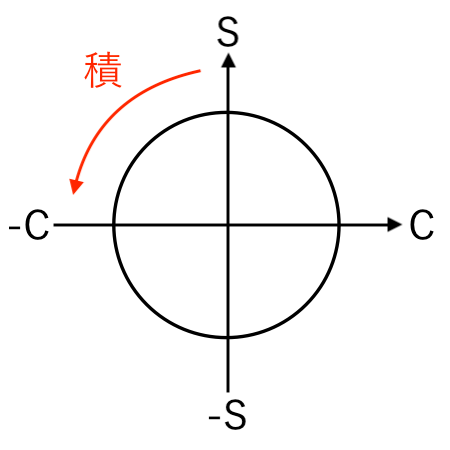
すると、
−C(−cos)
に移るので
cos の微分・積分
cos の微分:$ ( \cos x )’ = − \sin x $
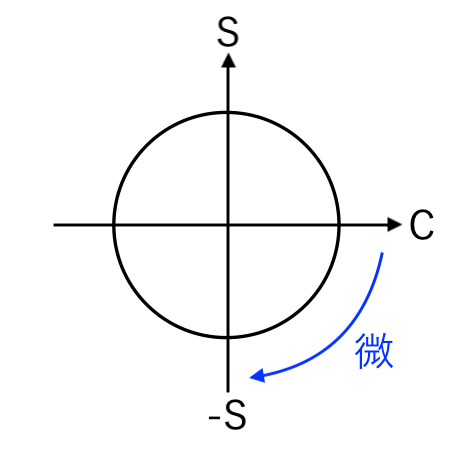
すると、
−S(−sin)
に移るので
となります。
cos の積分:$ \displaystyle{ \int \cos x \,dx = \sin x + C } $
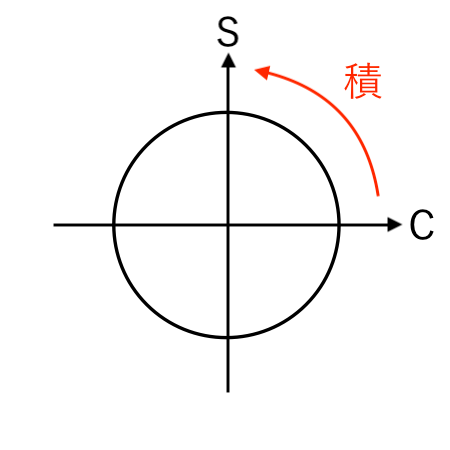
すると、
S(sin)
に移るので
−sin の微分・積分
−sin の微分:$ ( − \sin x )’ = − \cos x $
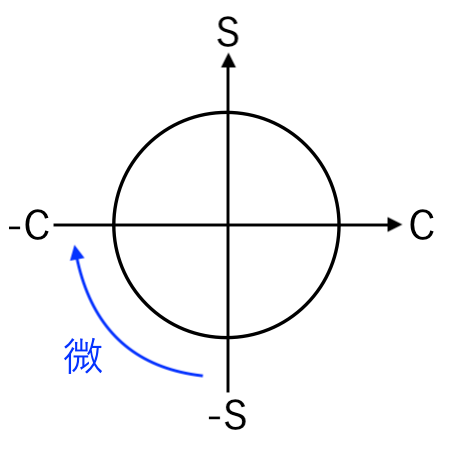
すると、
−C(−cos)
に移るので
となります。
−sin の積分:$ \displaystyle{ \int (− \sin x ) \,dx = \cos x + C } $
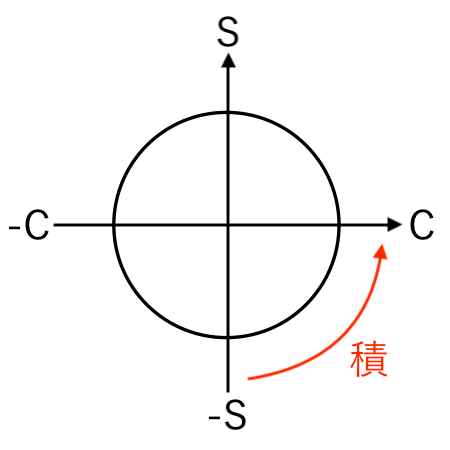
すると、
C(cos)
に移るので
−cos の微分・積分
−cos の微分:$ ( − \cos x )’ = \sin x $
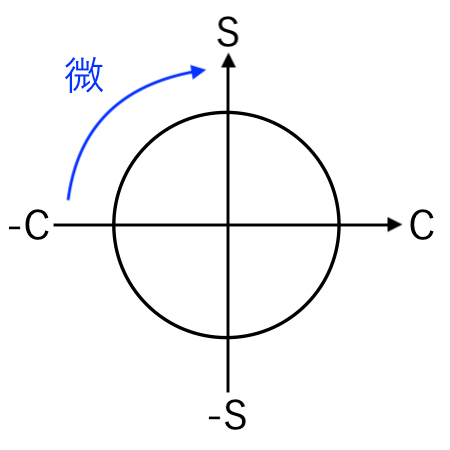
すると、
S(sin)
に移るので
となります。
−cos の積分:$ \displaystyle{ \int (− \cos x ) \,dx = − \sin x + C } $
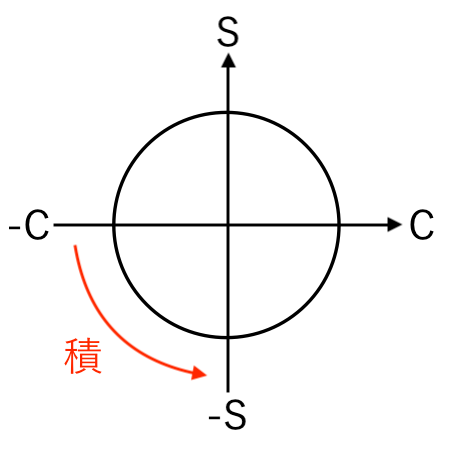
すると、
−S(−sin)
に移るので
【補足】−sin と −cos の微分・積分
−sin と −cos の微分・積分 については、以下のように計算してももちろんOK
- $ ( − \sin x )’ = −( \sin x )’ = − \cos x $
- $ \displaystyle{ \int (− \sin x ) \,dx = − \int \sin x \,dx }\\
\displaystyle{ = − (− \cos x ) + C = \cos x + C } $ - $ ( − \cos x )’ = −( \cos x )’ = −(−\sin x ) = \sin x $
- $ \displaystyle{ \int (− \cos x ) \,dx = − \int \cos x \,dx = − \sin x + C } $
ですが、今回紹介した方法に慣れるとスピードアップできます。
ぜひマスターしておきましょう!
【練習問題】sin と cos の微分・積分
sin と cos 微分・積分の裏ワザ を実際に使って、問題演習をしてみましょう。
まずは、下のような図を紙に描いておきます。
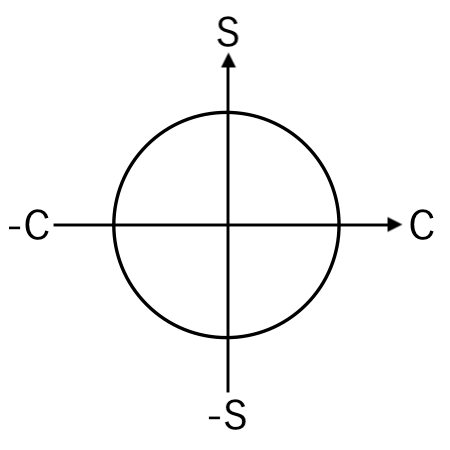
準備できたらスタート!
問題
(1) $ ( 2 \cos x )’ $
(2) $ ( − 5 \sin x )’ $
(3) $ ( − \cos 3x )’ $
(4) $ ( 2 \sin x − 3 \cos x )’ $
(5) $ \displaystyle{ \int (−\sin x + \cos x ) \,dx } $
(6) $ \displaystyle{ \int (−5 \cos x + 2 \sin x ) \,dx } $
(7) $ \displaystyle{ \int_0^{\pi \over 2} ( \sin x + \cos x ) \,dx } $
(8) $ \displaystyle{ \int_{\pi \over 3} ^{ {4 \over 3}\pi} ( \cos x −\sin x ) \,dx } $
解答
- 【解答・解説】を見る
-
【解答】
(1) $ − 2 \sin x $
(2) $− 5 \cos x $
(3) $ 3 \sin 3x $
(4) $ 2 \cos x −3 \sin x $
(5) $ \cos x + \sin x + C $($C$ は積分定数)
(6) $ −5 \sin x −2 \cos x + C $($C$ は積分定数)
(7) $2$
(8) $ − \sqrt{3}−1 $
【解説】
(1) $ ( 2 \cos x )’ = 2 ( \cos x )’ = − 2 \sin x $
(2) $ ( − 5 \sin x )’ = 5 ( − \sin x )’ = − 5 \cos x $
(3) $ ( − \cos 3x )’ = \sin 3x \cdot (3x)’ = 3 \sin 3x $ ← 合成関数の微分
(4) $ ( 2 \sin x + 3 \cos x )’ = 2(\sin x)’ + 3(\cos x)’ \\
= 2 \cos x −3 \sin x $(5) $ \displaystyle{ \int (−\sin x + \cos x ) \,dx \\
= \int (−\sin x) \,dx + \int \cos x \,dx \\
= \cos x + \sin x + C } $(6) $ \displaystyle{ \int (−5 \cos x + 2 \sin x ) \,dx \\
= 5 \int (−\cos x) \,dx + 2 \int \sin x \,dx \\
= −5 \sin x −2 \cos x + C } $(7) $ \displaystyle{ \int_0^{\pi \over 2} ( \sin x + \cos x ) \,dx = \left[ − \cos x + \sin x \right]_0^{\pi \over 2} }$
$ $ $ \displaystyle{ = \left( − \cos {\pi \over 2} + \sin {\pi \over 2} \right) − \left( − \cos 0 + \sin 0 \right) }$
$ $ $= 1 −(−1) = 2 $
(8) $ \displaystyle{ \int_{\pi \over 3} ^{ {4 \over 3}\pi} ( \cos x −\sin x ) \,dx = \left[ \sin x + \cos x \right]_{\pi \over 3}^{ {4 \over 3}\pi} }$
$ $ $ \displaystyle{ = \left( \sin { {4 \over 3}\pi} + \cos { {4 \over 3}\pi} \right) − \left( \sin {\pi \over 3} + \cos {\pi \over 3} \right) }$
$ $ $ \displaystyle{ = \left(− { \sqrt{3} \over 2 } −{1 \over 2}\right) −\left( { \sqrt{3} \over 2 } + {1 \over 2} \right) } $
$ $ $ \displaystyle{ = − \sqrt{3}−1 } $
以上です。お疲れ様でした!
【まとめ】sin と cos の微分・積分「裏ワザ」
最後に、三角関数の sinとcosの微分・積分 を一瞬で簡単にやる「裏ワザ」をまとめておきます。

【軸】
- 横軸:C(cos)
- 縦軸:S(sin)
【回転】
- 反時計回り(左回り) → 積分
- 時計回り(右回り) → 微分
何度も練習して、バッチリ使いこなせるようにしましょう!
質問・要望があれば気軽にコメントください👍
【数学I】sinとcosの変換「裏ワザ」
実は、数学Iの三角比「sinとcosの変換」にもこの「裏ワザ」が使えます。
sinとcosの変換公式がなかなか覚えられない! いちいち単位円をかいて変換公式を導くのも面倒だ・・・ sinとcosの変換を一瞬で&簡単にできる便利な方法はないの? こういった要望に応えます。 この[…]