「確率Pnが最大になるnの値」を求める問題がイマイチわからない
「玉やカードを同時に(一度に)取り出す問題」「サイコロとかの反復試行の問題」で一番ラクな解き方をわかりやすく教えてほしい!
こういったお悩みを解消します。
「確率 Pn の最大値を求める問題」は、国公立大・難関私立大の受験生なら必ずマスターしたい問題のひとつです。
一般的に難易度は高め(青チャート レベル5くらい)と言われていますが、実は「確率 Pn の最大値」の出題パターンによって ラクな解き方 が違います。
このことを知っておかないと、やたらと計算が大変な解き方をやってしまっている可能性もあります。
このページ読んで、しっかりマスターしておきましょう!!
【高校数学】確率 $P_n$ の最大値の求め方
「確率 Pn の最大値」を求める問題は、以下の 2通りの解き方があります。
- 差「$ P_{n+1}−P_n>0 $」となる $n$ を求める
- 比「$ \displaystyle{ { P_{n+1} \over P_n } > 1 } $」となる $n$ を求める
基本的にはどちらかの解き方をすればOKですが、
問題のパターンによってラクな解き方が決まっています。
「1回の試行」と「反復試行」パターンの問題に分けて解説します。
確率 $P_n$ の最大値を求める問題【1回の試行】
まずは「確率 Pn の最大値を求める問題」で「1回の試行」のパターンを解説します。
袋の玉を同時に(一度に)取り出す問題などが、このパターンに当てはまります。
実際に問題を解いてみましょう!
【例題1】赤玉 $7$ 個と白玉 $n$ 個($n≧2$)が入っている袋から、$5$ 個の玉を同時に取り出すとき、赤玉が $3$ 個で白玉が $2$ 個である確率を $P_n$ とする。
(1) 確率 $P_n$ を求めよ。
(2) 確率 $P_n$ が最大となる $n$ の値とその最大値を求めよ。 [類 10 富山大]
(1) 確率 $P_n$ を求めよ。
問題文を整理しましょう。
まず赤玉 $7$ 個と白玉 $n$ 個($n≧2$)が入っている袋があって

ここから $5$ 個の玉を同時に取り出すとき、赤玉が $3$ 個で白玉が $2$ 個である確率が $P_n$ です。
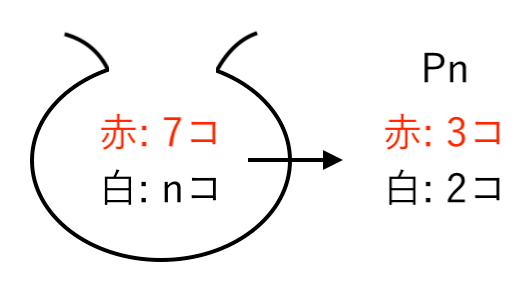
また、問題文に「同時に取り出す」とあるので「1回の試行」で操作を終えるパターンですね。
全事象は、合計 $(n+7)$ 個の玉から $5$ 個 取り出す方法(場合の数)なので
このうち、赤玉 $7$ 個から $3$ 個取り出す方法は
$ $ $ \displaystyle{ _7 C_3 = { 7 \cdot 6 \cdot 5 \over 3 \cdot 2 \cdot 1 } } $(通り)
白玉 $n$ 個から $2$ 個取り出す方法は
$ $ $ \displaystyle{ _n C_2 = { n (n−1) \over 2 } } $(通り)
なので、確率 $P_n$ は
$ \displaystyle{ P_n = { _7 C_3 \cdot _n C_2 \over _{n+7} C_5 } } $
$ $ $ \displaystyle{ = { \displaystyle{ { 7 \cdot 6 \cdot 5 \over 3 \cdot 2 \cdot 1 } \cdot { n (n−1) \over 2 } } \over \displaystyle{ { (n+7)(n+6)(n+5)(n+4)(n+3)\over 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 } } } } $
$ $ $ \displaystyle{ = { \displaystyle{ { 7 \cdot 6 \cdot 5 \over \require{cancel} \bcancel{3 \cdot 2 \cdot 1} } \cdot { n (n−1) \over \bcancel{2} } × 5 \cdot \bcancel{4 \cdot 3} \cdot 2 } \over \displaystyle{ { (n+7)(n+6)(n+5)(n+4)(n+3)\over \cancel{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} } × \cancel{5 \cdot 4 \cdot 3 \cdot 2} } } } $
$ $ $ \displaystyle{ = { 2100 \ n (n−1) \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
(注)ここでは、分母と分子の両方に「$5 \cdot 4 \cdot 3 \cdot 2$」をかけて計算しましたが、
$ $ $ \displaystyle{ P_n = { _7 C_3 \cdot _n C_2 \over \color{green}{_{n+7} C_5} } } $
$ $ $ \displaystyle{ = { _7 C_3 \cdot _n C_2 } \color{green}{× {1 \over _{n+7} C_5 } } } $
$ $ $ \displaystyle{ = { \displaystyle{ { 7 \cdot 6 \cdot 5 \over \require{cancel} \bcancel{3 \cdot 2 \cdot 1} } \cdot { n (n−1) \over \bcancel{2} } } } } $ $\displaystyle{ × { {5 \cdot \bcancel{ 4 \cdot 3 } \cdot 2 \cdot 1} \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
と考えてもOK。
解答をまとめると、こんな感じ。
- 【(1) 解答】を見る
-
【(1) 解答】
合計 $(n+7)$ 個の玉から $5$ 個 取り出す方法は
$ $ $ \displaystyle{ _{n+7} C_5 = { (n+7)(n+6)(n+5)(n+4)(n+3)\over 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 } } $(通り)
このうち、赤玉 $7$ 個から $3$ 個、白玉 $n$ 個から $2$ 個 取り出す方法は
$ $ $ \displaystyle{ _7 C_3 \cdot _n C_2 = { 7 \cdot 6 \cdot 5 \over 3 \cdot 2 \cdot 1 } \cdot { n (n−1) \over 2 } } $(通り)
なので、確率 $P_n$ は
$ \displaystyle{ P_n = { _7 C_3 \cdot _n C_2 \over _{n+7} C_5 } } $
$ $ $ \displaystyle{ = { \displaystyle{ { 7 \cdot 6 \cdot 5 \over 3 \cdot 2 \cdot 1 } \cdot { n (n−1) \over 2 } } \over \displaystyle{ { (n+7)(n+6)(n+5)(n+4)(n+3)\over 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 } } } } $
$ $ $ \displaystyle{ = { 2100 \ n (n−1) \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
(2) 確率 $P_n$ が最大となる $n$ の値とその最大値を求めよ。
「確率 Pn の最大値」を求めるために、まずは $P_{n+1}$ を求めます。
(1) の結果より
$ $ $ \displaystyle{ P_n = { 2100 \ n (n−1) \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
「$n$」を「$n+1$」に置き換えると
($n$ の数字が 1つ増える)
ここから「確率 Pn の最大値」を求める方法は、以下の 2通りあります。
- 差「$ P_{n+1}−P_n>0 $」となる $n$ を求める
- 比「$ \displaystyle{ { P_{n+1} \over P_n } > 1 } $」となる $n$ を求める
せっかくなので両方やってみます。
解き方① $ P_{n+1}−P_n>0 $ となる $n$ を求める
$ \displaystyle{ P_{n+1}−P_n }$
$ \displaystyle{ = { 2100 \ (n+1) n \over (n+8)(n+7)(n+6)(n+5)(n+4) } }$ $\displaystyle{ −{ 2100 \ n (n−1) \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
分母を無理やり揃える(通分する)と
$ \displaystyle{ = { 2100 \ (n+1) n \color{red}{(n+3)} \over (n+8)(n+7)(n+6)(n+5)(n+4) \color{red}{(n+3)} } }$ $\displaystyle{−{ 2100 \ n (n−1)\color{red}{(n+8)} \over \color{red}{(n+8)} (n+7)(n+6)(n+5)(n+4)(n+3) } } $
共通因数をくくり出すと
$ \displaystyle{ = { 2100 \ n \over (n+8)(n+7)(n+6)(n+5)(n+4)(n+3) } }$ $\displaystyle{ \left\{ (n+1) (n+3)−(n−1)(n+8) \right\} } $
$ \displaystyle{ = { 2100 \ n \over (n+8)(n+7)(n+6)(n+5)(n+4)(n+3) } }$ $\displaystyle{ \left( \bbox[#F4E2E2, 2pt, border:]{−3n +11 } \right) } $
ここで
$ $ $ \color{red}{ P_{n+1}−P_n > 0 } $
とすると、$n≧2$ より、常に
$ $ $ \displaystyle{ { 2100 \ n \over (n+8)(n+7)(n+6)(n+5)(n+4)(n+3) }> 0 } $
なので、結局
$ $ $ \bbox[#F4E2E2, 2pt, border:]{−3n +11 } > 0 $
$ $∴ $ \displaystyle{ n < {11 \over 3} = 3{2 \over 3} } $
$n$ は $2$ 以上の自然数より
$ $ $ \color{red}{ n = 2, 3 } $
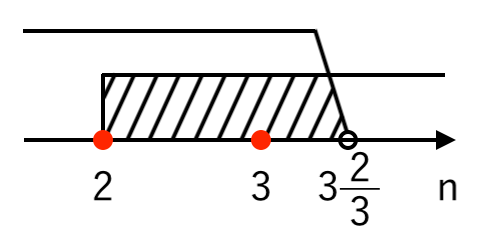
よって
逆に
$ $ $ \color{red}{ P_{n+1}−P_n<0 } $
とすると、不等号の向きが逆になるので
$ $ $ \displaystyle{ n >{11 \over 3} = 3{2 \over 3} } $
$ $∴ $ \color{red}{ n = 4, 5, 6, \cdots } $
よって
まとめて書くと
n = 2, 3 \enspace \enspace \enspace \enspace \, のとき \, \, P_n<P_{n+1} \, (単調増加)\\
\\
n = 4, 5, 6, \cdots \, のとき \, \, P_n>P_{n+1} \, (単調減少)\\
\end{cases}$
$n$ に値を 1個ずつ代入していくと
$ $ $ n=2$ のとき $P_2<P_3 $
$ $ $ n=3$ のとき $P_3<P_4 $
$ $ $ n=4$ のとき $P_4>P_5 $
$ $ $ n=5$ のとき $P_5>P_6 $
$ $ $ n=6$ のとき $P_6>P_7 $
$ $ $ \vdots $
これらを横につなげると
なので
$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=4} $
その最大値は
$ $ $ \displaystyle{ \color{red}{P_4} = { 2100 \cdot \color{red}{4} (\color{red}{4}−1) \over (\color{red}{4}+7)(\color{red}{4}+6)(\color{red}{4}+5)(\color{red}{4}+4)(\color{red}{4}+3) } } $
$ $ $ \displaystyle{ = { 2100 \cdot 4 \cdot 3 \over 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 } } $
$ $ $ \displaystyle{ = { 5 \over 11 } } $
これで 確率 $P_n$ の最大値が求められました。
「解き方①」の解答をまとめると、こんな感じ。
- 【(2) 解答①】を見る
-
【(2) 解答①】
$ \displaystyle{ P_{n+1}−P_n }$
$ \displaystyle{ = { 2100 \ (n+1) n \over (n+8)(n+7)(n+6)(n+5)(n+4) } }$ $\displaystyle{ −{ 2100 \ n (n−1) \over (n+7)(n+6)(n+5)(n+4)(n+3) } } $
$ \displaystyle{ = { 2100 \ n \over (n+8)(n+7)(n+6)(n+5)(n+4)(n+3) } }$ $\displaystyle{ \left( \bbox[#F4E2E2, 2pt, border:]{−3n +11 } \right) } $
なので
$ \begin{cases}
n = 2, 3 \enspace \enspace \enspace \enspace \, のとき \, P_{n+1}−P_n>0 \, \Leftrightarrow \, P_n<P_{n+1} \\
\\
n = 4, 5, 6, \cdots \, のとき \, P_{n+1}−P_n<0 \, \Leftrightarrow \, P_n>P_{n+1} \\
\end{cases}$$ $∴ $ P_2<P_3<\color{red}{P_4}>P_5>P_6>P_7> \cdots $
よって、$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=4} $
その最大値は
$ $ $ \displaystyle{ \color{red}{P_4} = { 2100 \cdot \color{red}{4} (\color{red}{4}−1) \over (\color{red}{4}+7)(\color{red}{4}+6)(\color{red}{4}+5)(\color{red}{4}+4)(\color{red}{4}+3) } } $
$ $ $ \displaystyle{ = { 2100 \cdot 4 \cdot 3 \over 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 } } $
$ $ $ \displaystyle{ = { 5 \over 11 } } $
解き方② $ \displaystyle{ { P_{n+1} \over P_n } > 1 } $ となる $n$ を求める
$ \displaystyle{ { P_{n+1} \over P_n } } $
$ \displaystyle{ = { P_{n+1} × {1 \over P_n} } } $
$ \displaystyle{ = { 2100 \ (n+1) n \over (n+8)(n+7)(n+6)(n+5)(n+4) } }$ $ \displaystyle{ ×{ (n+7)(n+6)(n+5)(n+4)(n+3) \over 2100 \ n (n−1) } } $
$ \displaystyle{ = { \require{cancel} \bcancel{ 2100 } \ (n+1) \bcancel{ n } \over (n+8) \cancel{ (n+7)(n+6)(n+5)(n+4) } } }$ $ \displaystyle{ × { \cancel{ (n+7)(n+6)(n+5)(n+4) } (n+3) \over \bcancel{ 2100 } \ \bcancel{ n } (n−1) } } $
$ \displaystyle{ = { (n+1)(n+3) \over (n+8)(n−1) } } $
ここで
$ $ $ \displaystyle{ \color{red}{ { P_{n+1} \over P_n } > 1 } } $
とすると
$ $ $ \displaystyle{ { (n+1)(n+3) \over (n+8)(n−1) }> 1 } $
$n≧2$ より $ (n+8)(n−1) \ >0$ なので
両辺に $ (n+8)(n−1) \ (>0)$ をかけて
$ $ $ \displaystyle{ (n+1)(n+3)> (n+8)(n−1) } $
$ $∴ $ \displaystyle{ n^2 + 4n + 3 > n^2 +7n −8 } $
$ $∴ $ \displaystyle{ 11 > 3n } $
$ $∴ $ \displaystyle{ n<{11 \over 3}= 3{2 \over 3} } $
$n$ は $2$ 以上の自然数より
$ $ $ \color{red}{ n = 2, 3 } $

よって
逆に
$ $ $ \displaystyle{ \color{red}{ { P_{n+1} \over P_n } < 1 } } $
とすると、不等号の向きが逆になるので
$ $ $ \displaystyle{ n >{11 \over 3} = 3{2 \over 3} } $
$ $∴ $ \color{red}{ n = 4, 5, 6, \cdots } $
よって
ここまで出来たら、あとは「解き方①」と同様です。
n = 2, 3 \enspace \enspace \enspace \enspace \, のとき \, \, P_n<P_{n+1} \, (単調増加)\\
\\
n = 4, 5, 6, \cdots \, のとき \, \, P_n>P_{n+1} \, (単調減少)\\
\end{cases}$
ゆえに
なので
$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=4} $
その最大値は
$ $ $ \displaystyle{ \color{red}{P_4} = { 2100 \cdot \color{red}{4} (\color{red}{4}−1) \over (\color{red}{4}+7)(\color{red}{4}+6)(\color{red}{4}+5)(\color{red}{4}+4)(\color{red}{4}+3) } } $
$ $ $ \displaystyle{ = { 2100 \cdot 4 \cdot 3 \over 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 } } $
$ $ $ \displaystyle{ = { 5 \over 11 } } $
こんな流れでも 確率 $P_n$ の最大値を求められます。
「解き方②」の解答をまとめると、こんな感じ。
- 【(2) 解答②】を見る
- 【(2) 解答②】
$ \displaystyle{ { P_{n+1} \over P_n } } $
$ \displaystyle{ = { 2100 \ (n+1) n \over (n+8)(n+7)(n+6)(n+5)(n+4) } }$ $ \displaystyle{ ×{ (n+7)(n+6)(n+5)(n+4)(n+3) \over 2100 \ n (n−1) } } $
$ \displaystyle{ = { (n+1)(n+3) \over (n+8)(n−1) } } $
$ \displaystyle{ = { n^2 + 4n + 3 \over n^2 +7n −8 } } $
なので
$ \begin{cases}
n = 2, 3 \enspace \enspace \enspace \enspace \, のとき \, \displaystyle{ { P_{n+1} \over P_n } > 1 } \, \Leftrightarrow \, P_n<P_{n+1} \\
\\
n = 4, 5, 6, \cdots \, のとき \, \displaystyle{ { P_{n+1} \over P_n } <1 } \, \Leftrightarrow \, P_n>P_{n+1} \\
\end{cases}$$ $∴ $ P_2<P_3<\color{red}{P_4}>P_5>P_6>P_7> \cdots $
$ $ $\vdots$
結論:「1回の試行」パターンは 解き方①、② どっちもOK!
「解き方①」と「解き方②」では、どっちがラクでしたか?
個人的には、正直あまり差はないように思います。
なので、「解き方①」「解き方②」の好きな方で解けばOKです。
ただし、問題文に「$ P_{n+1}−P_n > 0 $ となる $n$ を求めよ。」などの指示があればそれに従いましょう。
確率 $P_n$ の最大値を求める問題【反復試行】
次に「確率 Pn の最大値を求める問題」で「反復試行」のパターンを解説します。
袋の玉を繰り返し取り出したり、サイコロを何回も投げたりするような「同じ操作(試行)を繰り返す問題」が、このパターンに当てはまります。
【例題2】袋の中に赤玉 $60$ 個、白玉 $10$ 個が入っている。この袋から $1$ 個ずつ取り出して色を調べては戻すという試行を $40$ 回行う。赤玉が $n$ 回($0≦n≦40$)取り出される確率を $P_n$ とする。
(1) 確率 $P_n$ を求めよ。
(2) 確率 $P_n$ が最大となる $n$ の値を求めよ。 [類 群馬大]
(1) 確率 $P_n$ を求めよ。
赤玉 $60$ 個、白玉 $10$ 個が入っている袋があって

この袋から $1$ 個 取り出したとき、それが赤玉である確率は
$ $ $ \displaystyle{ {60 \over 70} = {6 \over 7} } $
白玉である確率は
$ $ $ \displaystyle{ {10 \over 70} = {1 \over 7} } $
です。
$計:70個$ $ \begin{cases}
\color{red}{赤}:60個 \, \cdots \displaystyle{ {60 \over 70} = {6 \over 7} } \\
\\
白:10個 \, \cdots \displaystyle{ {10 \over 70} = {1 \over 7} } \\
\end{cases}$
確率 $P_n$ は、$40$ 回のうち、赤玉が $n$ 回、白玉が $(40−n)$ 回 取り出される確率なので
$ \displaystyle{ P_n = \, _{40} C_n \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
$ $ $ \displaystyle{ = { 40! \over n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $ $(0≦n≦40)$
(注)$ \displaystyle{ _n C_r = {_n P_r \over r!} = { n! \over r! \, (n−r)!} } $ $\left( 0≦r≦n \right)$
解答としては、こんな感じ。
- 【(1) 解答】を見る
-
【(1) 解答】
$計:70個$ $ \begin{cases}
\color{red}{赤}:60個 \, \cdots \displaystyle{ {60 \over 70} = {6 \over 7} } \\
\\
白:10個 \, \cdots \displaystyle{ {10 \over 70} = {1 \over 7} } \\
\end{cases}$$P_n$ は、$40$ 回のうち、赤玉が $n$ 回、白玉が $(40−n)$ 回 取り出される確率なので
$ \displaystyle{ P_n = \, _{40} C_n \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
$ $ $ \displaystyle{ = { 40! \over n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $ $(0≦n≦40)$
(2) 確率 $P_n$ が最大となる $n$ の値を求めよ。
「確率 Pn の最大値」を求めるために、まずは $P_{n+1}$ を出しておくんでしたね。
(1) の結果より
$ $ $ \displaystyle{ P_n = { 40! \over n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
「$n$」を「$n+1$」に置き換えると
- 差「$ P_{n+1}−P_n>0 $」となる $n$ を求める
- 比「$ \displaystyle{ { P_{n+1} \over P_n } > 1 } $」となる $n$ を求める
解き方① $ P_{n+1}−P_n>0 $ となる $n$ を求める
$ \displaystyle{ P_{n+1}−P_n }$
$ \displaystyle{ = { 40! \over (n+1)! \, (39−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} }$ $ \displaystyle{−{ 40! \over n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
(無理やり)分母を揃えると
$ \displaystyle{ = { 40! \, \color{red}{(40−n)} \over (n+1)! \, \color{red}{(40−n)} \, (39−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} }$ $ \displaystyle{−{ 40! \, \color{red}{(n+1)} \over \color{red}{(n+1)} \, n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
$ \displaystyle{ = { 40! \, (40−n) \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} }$ $ \displaystyle{ −{ 40! \, (n+1) \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
(無理やり)共通因数をくくり出すと
$ \displaystyle{ = { 40! \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n} \left( {1 \over 7} \right)^{39−n} }$ $ \displaystyle{ \left\{ (40−n) \cdot {6 \over 7} − (n+1) {1 \over 7} \right\} } $
$ \displaystyle{ = { 40! \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n} \left( {1 \over 7} \right)^{40−n} }$ $ \displaystyle{ \left\{ (40−n) \cdot 6 − (n+1) \right\} } $
$ \displaystyle{ = { 40! \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n} \left( {1 \over 7} \right)^{40−n} }$ $ \displaystyle{ \left( \bbox[#F4E2E2, 2pt, border:]{ 239 −7n } \right) } $ $(0≦n≦39)$
ここで
$ $ $ \color{red}{ P_{n+1}−P_n > 0 } $
とすると、$0≦n≦39$ より、常に
$ $ $ \displaystyle{ { 40! \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n} \left( {1 \over 7} \right)^{40−n}> 0 } $
(注)$n=39$ のときが少し不安なので、パッと代入して確認すると
$ $ $ \displaystyle{ { 40! \over 40! \, \color{red}{1!} } \cdot \left( {6 \over 7} \right)^{39} \cdot \left( {1 \over 7} \right)^{1} } $
$ $ $ \displaystyle{ = { 40! \over 40! \, \cdot \color{red}{1} } \cdot \left( {6 \over 7} \right)^{39} \cdot \left( {1 \over 7} \right)> 0 } $ OK!
なので、結局
$ $ $ \bbox[#F4E2E2, 2pt, border:]{ 239 −7n }> 0 $
であればよいわけです。
$ $∴ $ \displaystyle{ n < { 239 \over 7 } = 34{ 1 \over 7 } } $
$n$ は $0≦n≦39$ をみたす整数なので
$ $ $ \color{red}{n = 0, 1, 2, \cdots , 34} $
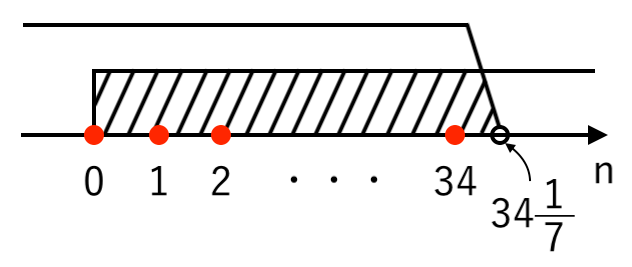
よって
逆に
$ $ $ \color{red}{ P_{n+1}−P_n < 0 } $
とすると、不等号の向きが逆になるので
$ $∴ $ \displaystyle{ n > { 239 \over 7 } = 34{ 1 \over 7 } } $
$ $∴ $ \color{red}{n = 35, 36, 37, 38, 39} $
よって
まとめて書くと
n = 0, 1, 2, \cdots , 34 \enspace \enspace \, のとき \, \, P_n<P_{n+1} \, (単調増加)\\
\\
n = 35, 36, 37, 38, 39 \, のとき \, \, P_n>P_{n+1} \, (単調減少)\\
\end{cases}$
ゆえに
なので
$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=35} $
これで $P_n$ が最大となる $n$ の値が求められました。
この解法だと、少し計算が大変でしたね・・・
「解き方①」の解答をまとめると、こんな感じ。
- 【(2) 解答①】を見る
-
【(2) 解答①】
$ \displaystyle{ P_{n+1}−P_n }$
$ \displaystyle{ = { 40! \over (n+1)! \, (39−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} }$ $ \displaystyle{−{ 40! \over n! \, (40−n)! } \cdot \left( {6 \over 7} \right)^n \left( {1 \over 7} \right)^{40−n} } $
$ \displaystyle{ = { 40! \over (n+1)! \, (40−n)! } \cdot \left( {6 \over 7} \right)^{n} \left( {1 \over 7} \right)^{40−n} }$ $ \displaystyle{ \left( \bbox[#F4E2E2, 2pt, border:]{ 239 −7n } \right) } $
なので
$ \begin{cases}
n = 0, 1, 2, \cdots , 34 \enspace \enspace \, のとき \, P_{n+1}−P_n > 0 \, \Leftrightarrow \, P_n<P_{n+1} \, \\
\\
n = 35, 36, 37, 38, 39 \, のとき \, P_{n+1}−P_n < 0 \, \Leftrightarrow \, P_n>P_{n+1} \\
\end{cases}$$ $∴ $ P_0<P_1<P_2<\cdots<P_{34}<\color{red}{P_{35}}>P_{36}>P_{37}>P_{38}>P_{39}>P_{40} $
よって、$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=35} $
解き方② $ \displaystyle{ { P_{n+1} \over P_n } > 1 } $ となる $n$ を求める
$ \displaystyle{ { P_{n+1} \over P_n } } $
$ \displaystyle{ = { P_{n+1} ×{1 \over P_n} } } $
$ \displaystyle{ = { { 40! \over (n+1)! \, (39−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} } }$ $ \displaystyle{ ×{ n! \, (40−n)! \over 40! } \cdot \left( {7 \over 6} \right)^n \cdot 7^{40−n} } $
$ \displaystyle{ = { { \require{cancel} \bcancel{40!} \over (n+1)\cancel{!} \, \bcancel{(39−n)!} } \cdot \left( {6 \over 7} \right)^\cancel{n+1} \cancel{ \left( {1 \over 7} \right)^{39−n} } } } $ $ \displaystyle{×{ \cancel{n!} \, (40−n)\bcancel{!} \over \bcancel{40!} } \cdot \cancel{ \left( {7 \over 6} \right)^n} \cdot 7^\cancel{40−n} } $
$ \displaystyle{ = { 6(40−n) \over {n+1} } } $
ここで
$ $ $ \displaystyle{ \color{red}{ { P_{n+1} \over P_n } > 1 } } $
とすると
$ $ $ \displaystyle{ { 6(40−n) \over {n+1} } > 1 } $
両辺に $(n+1) \ (>0)$ をかけて
$ $ $ \displaystyle{ 6(40−n) > n+1 } $
$ $∴ $ \displaystyle{ n <{239 \over 7} = 34{1 \over 7} } $
$n$ は $0≦n≦39$ をみたす整数なので
$ $ $ \color{red}{n = 0, 1, 2, \cdots , 34} $

よって
逆に
$ $ $ \color{red}{ P_{n+1}−P_n < 0 } $
とすると、不等号の向きが逆になるので
$ $∴ $ \displaystyle{ n > { 239 \over 7 } = 34{ 1 \over 7 } } $
$ $∴ $ \color{red}{n = 35, 36, 37, 38, 39} $
よって
ここまで出来たら、あとは「解き方①」と同様です。
n = 0, 1, 2, \cdots , 34 \enspace \enspace \, のとき \, \, P_n<P_{n+1} \, (単調増加)\\
\\
n = 35, 36, 37, 38, 39 \, のとき \, \, P_n>P_{n+1} \, (単調減少)\\
\end{cases}$
ゆえに
なので
$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=35} $
以上です。
「解き方②」の解答をまとめると、こんな感じ。
- 【(2) 解答②】を見る
-
【(2) 解答②】
$ \displaystyle{ { P_{n+1} \over P_n } } $
$ \displaystyle{ = { { 40! \over (n+1)! \, (39−n)! } \cdot \left( {6 \over 7} \right)^{n+1} \left( {1 \over 7} \right)^{39−n} } } $ $ \displaystyle{×{ n! \, (40−n)! \over 40! } \cdot \left( {7 \over 6} \right)^n \cdot 7^{40−n} } $
$ \displaystyle{ = { 6(40−n) \over {n+1} } } $
なので
$ \begin{cases}
n = 0, 1, 2, \cdots , 34 \enspace \enspace \, のとき \, \displaystyle{ { P_{n+1} \over P_n }>1} \, \Leftrightarrow \, P_n<P_{n+1} \, \\
\\
n = 35, 36, 37, 38, 39 \, のとき \, \displaystyle{ { P_{n+1} \over P_n }<1} \, \Leftrightarrow \, P_n>P_{n+1} \\
\end{cases}$$ $∴ $ P_0<P_1<P_2<\cdots<P_{34}<\color{red}{P_{35}}>P_{36}$ $>P_{37}>P_{38}>P_{39}>P_{40} $
よって、$P_n$ が最大となる $n$ の値は
$ $ $ \color{red}{n=35} $
結論:「反復試行」パターンは 解き方② がラク!
「解き方①」と「解き方②」では、どっちがラクでしたか?
おそらくほとんどの人が「解き方②」の方が簡単だな、と感じたと思います。
「確率 Pn の最大値を求める問題」の「反復試行」パターンは
解き方② $ \displaystyle{ \left( 比: { P_{n+1} \over P_n } > 1 \right) } $で解く!と覚えておきましょう。
【まとめ】確率 $P_n$ の最大値の求め方
最後にまとめです。
「確率 Pn の最大値を求める問題」の解き方は、以下の 2通り。
- 差「$ P_{n+1}−P_n>0 $」となる $n$ を求める
- 比「$ \displaystyle{ { P_{n+1} \over P_n } > 1 } $」となる $n$ を求める
「1回の試行」パターン: 解き方①、② どっちでもOK!
「反復試行」パターン: 解き方② $ \displaystyle{ \left( { P_{n+1} \over P_n } > 1 \right) } $で解く!
質問・要望があれば気軽にコメントください👍
