【高校数学】さいころの最大値・最小値の確率「公式」を伝授！【応用・入試問題つき】

「さいころの最大値・最小値の確率」の求め方がよく分からない

どうやって考えたらスラスラ解けるようになるの？

簡単に解く方法や、便利な公式があれば分かりやすく教えてほしい！

こういった要望に応えます。

「さいころの最大値・最小値の確率」を求める問題は、国公立大・難関大レベル を目指す受験生なら、必ずマスターしておかなければいけません。

このページを読めば

• 「さいころの最大値・最小値の確率」の簡単な求め方（公式）
• わかりやすいベン図などの書き方
• さいころの応用・入試問題の解き方

がマスターできます。

さいころの最大値の確率

まずは「さいころの 最大値 の確率」から見ていきましょう。

【例題1】$3$ 個のさいころを同時に投げるとき、次の確率を求めよ。

解説しやすいように、$3$ 個のさいころを投げたときの「出た目の最大値」を $ \color{red}{M} $ とします。

(1) 出た目の最大値が $5$ 以下

そもそも「出た目の 最大値 が 5 以下 $(M≦5)$」とはどういう意味でしょうか？

例えば

のように「出た目が 1〜5」ということです。

さいころ $1$ 個を投げるとき、1〜5 の目 が出る確率は

$ $　$ \displaystyle{ {( 1〜5 \ の目 ) \over ( 1〜6 \ の目 ) } \enspace \enspace = {5 \over 6} } $

よって、さいころ $3$ 個を投げるとき

「出た目の 最大値 が 5 以下になる確率 $ P(M≦5) $」は

「さいころ $3$ 個とも 1〜5 の目 が出る確率」なので

(2) 出た目の最大値が $4$ 以下

(1) と同様に考えると「出た目の 最大値 が 4 以下 $(M≦4)$」というのは、

先ほどの例のうち

のように「出た目が 1〜4」という意味です。

さいころ $1$ 個を投げるとき、1〜4 の目 が出る確率は

$ $　$ \displaystyle{ {( 1〜4 \ の目 ) \over ( 1〜6 \ の目 ) } \enspace \enspace = {4 \over 6} = {2 \over 3} } $

よって、さいころ $3$ 個を投げるとき

「出た目の 最大値 が 4 以下になる確率 $ P(M≦4) $」は

「さいころ $3$ 個とも 1〜4 の目 が出る確率」なので

(3) 出た目の最大値が $5$

「出た目の 最大値 が 5 $(M=5)$」は

最初に挙げた例のうち 一番上の

だけなので

「(3)出た目の最大値が 5」$=$「(1)最大値が 5 以下」$−$「(2)最大値が 4 以下」

を計算すればいいわけです。

よって、さいころ $3$ 個を投げるとき

「出た目の 最大値 が 5 である確率 $ P(M=5) $」は

ベン図で考えると

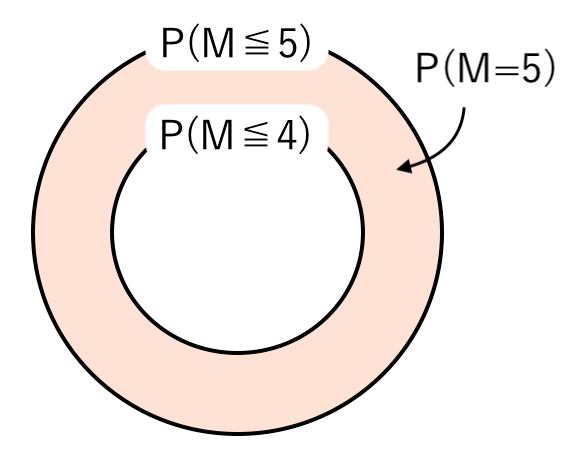
【公式】出た目の最大値 $M$ が $k$ である確率 $P(M=k)$

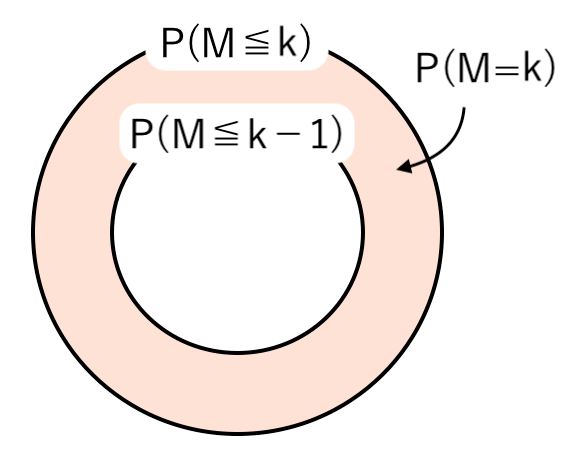
まとめると

「出た目の最大値が $k$」$=$「最大値が $k$ 以下」$−$「最大値が $(k−1)$ 以下」

より、次の公式が成り立ちます。

使い方

例えば、さっきの 問題(3) に当てはめると

$n=3, \ k=5$ より

注意点

「出た目の最大値が $1$」のときは要注意！

$k=1$ とすると

（注）「出た目の最大値が $0$ 以下」になることはあり得ないので

$ $　$P(M≦0) = 0 $

さいころの最小値の確率

次に「さいころの 最小値 の確率」を解説します。

【例題2】$3$ 個のさいころを同時に投げるとき、次の確率を求めよ。

解説しやすいように、$3$ 個のさいころを投げたときの「出た目の最小値」を $ \color{blue}{m} $ とします。

(1) 出た目の最小値が $3$ 以上

「出た目の 最小値 が 3 以上 $(m≧3)$」とは、例えば

のように「出た目が 3〜6」という意味です。

さいころ $1$ 個を投げるとき、3〜6の目 が出る確率は

$ $　$ \displaystyle{ {( 3〜6 \ の目 ) \over ( 1〜6 \ の目 ) } \enspace \enspace = {4 \over 6} = {2 \over 3} } $

よって、さいころ $3$ 個を投げるとき

「出た目の 最小値 が 3 以上になる確率 $ P(m≧3) $」は

「さいころ $3$ 個とも 3〜6の目 が出る確率」なので

(2) 出た目の最小値が $4$ 以上

「出た目の 最小値 が 4 以上 $(m≧4)$」とは、例えば

のように「出た目が 4〜6」ということです。

さいころ $1$ 個を投げるとき、4〜6の目 が出る確率は

$ $　$ \displaystyle{ {( 4〜6 \ の目 ) \over ( 1〜6 \ の目 ) } \enspace \enspace = {3 \over 6} = {1 \over 2} } $

よって、さいころ $3$ 個を投げるとき

「出た目の 最小値 が 4 以上になる確率 $ P(m≧4) $」は

「さいころ $3$ 個とも 4〜6の目 が出る確率」なので

(3) 出た目の最小値が $3$

「出た目の 最小値 が 3 $(m=3)$」は

最初に挙げた例のうち 一番上の

だけなので

「(3)出た目の最小値が 3」$=$「(1)最小値が 3 以上」$−$「(2)最小値が 4 以上」

を計算すればいいわけです。

よって、さいころ $3$ 個を投げるとき

「出た目の 最小値 が 3 である確率 $ P(m=3) $」は

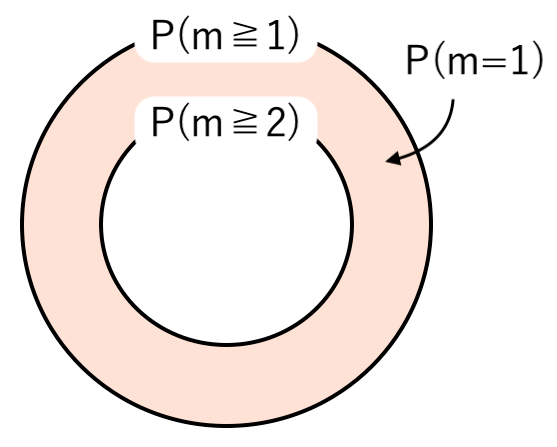
ベン図で考えると

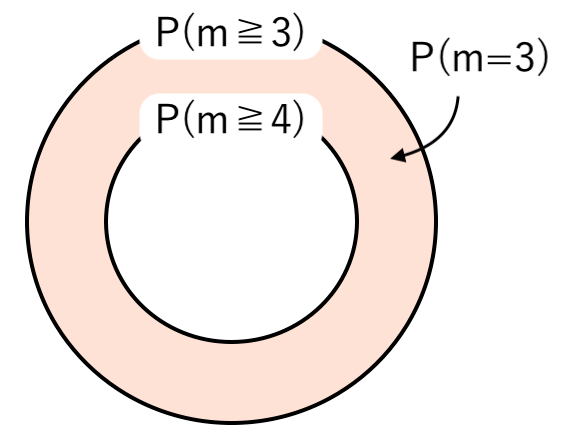
【公式】出た目の最小値 $m$ が $k$ である確率 $P(m=k)$

まとめると

「出た目の最小値が $k$」$=$「最小値が $k$ 以上」$−$「最小値が $(k+1)$ 以上」

より、次の公式が成り立ちます。

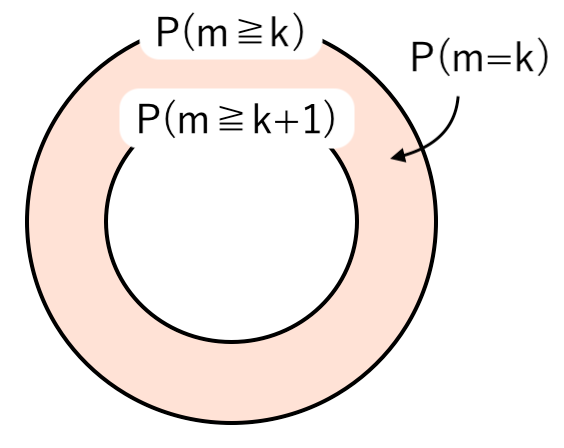
使い方

例えば、さっきの 問題(3) で言うと

$n=3, \ k=3$ とすればよいので

注意点

「出た目の最小値が $6$」のときは

$k=6$ とすると

（注）「出た目の最小値が $7$ 以上」になることはあり得ないので

$ $　$P(m≧7) = 0 $

さいころの最大値・最小値の確率【入試問題】

「さいころの最大値・最小値の確率」を学んだところで、少し難しめの入試問題にチャレンジです！

旧帝大・難関大の標準レベル の問題です。

【問題】さいころを $n$ 回投げる試行を考える。

(1) 出る目の最小値が $1$ である確率を求めよ。

今回のおさらいですね。学んだことを思い出しながら解いてみましょう。

【解答・解説】を見る

【解答】

さいころを $n$ 回投げるとき、出る目の最小値 $m$ が $k$ である確率を $P(m=k)$ とすると

$ $　$P(m=1) = P(m≧1) − P(m≧2)$

$ $　　　　　$ \displaystyle{ = \left( {6 \over 6} \right)^n − \left( {5 \over 6} \right)^n } $

$ $　　　　　$ \displaystyle{ = 1 − \left( {5 \over 6} \right)^n } $

（注）ベン図

(2) 出る目の最小値が $1$ で、かつ最大値が $6$ である確率を求めよ。

一気に求めるのではなく、順序立てて計算していきましょう。

【解答・解説】を見る

【解答】

さいころを $n$ 回投げるとき、出る目の最大値 $M$ が $k$ である確率を $P(M=k)$ とすると

$ $　$P(M=6) = P(M≦6) − P(M≦5)$

$ $　　　　　$ \displaystyle{ = \left( {6 \over 6} \right)^n − \left( {5 \over 6} \right)^n } $

$ $　　　　　$ \displaystyle{ = 1 − \left( {5 \over 6} \right)^n } $

 

また、さいころを $n$ 回投げるとき

$ \begin{cases}
事象 A 「出る目の最小値が \ 1」 \\
\\
事象 B「出る目の最大値が \ 6」 \\
\end{cases}$

とすると

$ \begin{cases}
\displaystyle{ P(A) = P(m=1) = 1 − \left( {5 \over 6} \right)^n } \\
\\
\displaystyle{ P(B) = P(M=6) = 1 − \left( {5 \over 6} \right)^n }  \\
\end{cases}$

 

よって、「出る目の最小値が $1$」かつ「出る目の最大値が $6$」である確率は

$ $　$ P(A \cap B) = P(A) + P(B) − P(A \cup B) $ ・・・（注1）

$ $　$ = P(A) + P(B) − \left\{ 1 − P( \overline{A \cup B} ) \right\} $ ・・・（注2）

$ $　$ = P(A) + P(B) − \left\{ 1 − P( \overline{A} \cap \overline{B} ) \right\} $ ・・・（注3）

$ $　$ = P(A) + P(B) + P( \overline{A} \cap \overline{B} ) − 1 $

 

ここで、$P( \overline{A} \cap \overline{B} )$ は

「出る目の最小値が $2$ 以上、かつ最大値が $6$ 以下である確率」

すなわち

「出る目が $2$〜$5$ である確率」

なので

$ $　$ \displaystyle{ P( \overline{A} \cap \overline{B} ) = \left( {4 \over 6} \right)^n = \left( {2 \over 3} \right)^n} $

 

したがって、求める確率は

$ $　$ P(A \cap B) = P(A) + P(B) + P( \overline{A} \cap \overline{B} ) − 1 $

$ $　　　　$ \displaystyle{ = 2 \left\{ 1 − \left( {5 \over 6} \right)^n \right\} + \left( {2 \over 3} \right)^n − 1 } $

$ $　　　　$ \displaystyle{ = 1 + \left( {2 \over 3} \right)^n − 2 \left( {5 \over 6} \right)^n } $

（注1, 2）集合の性質（個数定理）

$ $　$ P(A \cap B) = P(A) + P(B) − P(A \cup B) $

$ $　$ P(\overline{A}) = P(U) − P(A) = 1 − P(A) $

（注3）ド・モルガンの法則

$ $　$P( \overline{A \cup B} ) = P( \overline{A} \cap \overline{B} ) $

$ $　$P( \overline{A \cap B} ) = P( \overline{A} \cup \overline{B} ) $

以上です。お疲れ様でした！

【まとめ】さいころの最大値・最小値の確率

最後にまとめです。

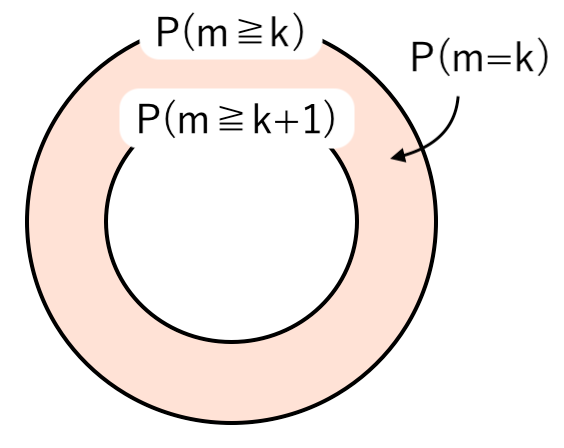
いつでもベン図などをかいて導けるように、考え方を覚えておきましょう！

質問・要望があれば気軽にコメントください👍